<- previous index next ->
Some volumes and areas you should already know:
x1,y1
/\
/ \
x3,y3 /___ \ x2,y2
area of a triangle is 1/2 base times height
| 1 1 1 | | 1 x1 y1 |
area of a triangle is 1/2 det| x1 x2 x3 | = 1/2 det| 1 x2 y2 |
| y1 y2 y3 | | 1 x3 y3 |
area of a triangle is |(V2 - V1) x (V3 - V1)| length of cross product
area of a rectangle is base times height
area of a parallelogram is base times height
area of a circle is Pi r^2
area.txt more area and volume formulas
Some variations that you may need some day:
You may not know the area of a five point star inscribed in
a unit circle or the area of an arbitrary closed polygon.
Easy to calculate, using the Sailors Algorithm:
Given the n points (x,y) of a closed polygon where no edges cross,
compute the sum i=1..n (x_i+1 - x_i) * (y_i+1 + y_i)/2
(The first point is repeated as the n+1 point,
add enough to the y's to make them all positive)
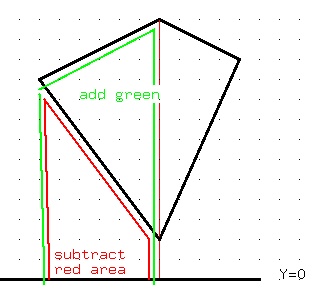 The intuition for the Sailors Algorithm, on a shape with only
vertical and horizontal edges is:
a vertical line adds no area
a horizontal line to the right adds area (length times average height)
a horizontal line to the left subtracts area.
The computed area will be positive if an upper outside edge is
listed in counter clockwise order, else negative, take absolute value.
A sample program is:
area2_dat.py3 source code
star.dat input
area2_dat_py3.out output
poly_area.c
poly_area_maze.out
maze.path
poly_area_star.out
star.path
sailors_area.java
sailors_area_java.out
The maze (8 units wide, 7 units high, area is 35) is:
The intuition for the Sailors Algorithm, on a shape with only
vertical and horizontal edges is:
a vertical line adds no area
a horizontal line to the right adds area (length times average height)
a horizontal line to the left subtracts area.
The computed area will be positive if an upper outside edge is
listed in counter clockwise order, else negative, take absolute value.
A sample program is:
area2_dat.py3 source code
star.dat input
area2_dat_py3.out output
poly_area.c
poly_area_maze.out
maze.path
poly_area_star.out
star.path
sailors_area.java
sailors_area_java.out
The maze (8 units wide, 7 units high, area is 35) is:
 The star (inscribed in a circle with radius 5, area about 28.06) is:
The star (inscribed in a circle with radius 5, area about 28.06) is:
 Volume of a sphere 4/3 Pi r^3
Area of a sphere 4 Pi r^2
Volume of a cone, tetrahedron, any solid with a planar base that goes
to a point 1/3 base area times height
| 1 x1 y1 z1 |
Volume of a tetrahedron 1/6 det | 1 x2 y2 z2 |
| 1 x3 y3 z3 |
| 1 x4 y4 z4 |
using just the x,y,z of the four vertices t1, t2, t3, t4
t4
/\
/ \ missing line from t2 to t4
/ \
/______\
t1\ /t3
\ /
\ /
\/
t2
four surface triangles t1 t2 t3, t1 t2 t4, t1 t3 t4, t2 t3 t4
Volume of a sphere 4/3 Pi r^3
Area of a sphere 4 Pi r^2
Volume of a cone, tetrahedron, any solid with a planar base that goes
to a point 1/3 base area times height
| 1 x1 y1 z1 |
Volume of a tetrahedron 1/6 det | 1 x2 y2 z2 |
| 1 x3 y3 z3 |
| 1 x4 y4 z4 |
using just the x,y,z of the four vertices t1, t2, t3, t4
t4
/\
/ \ missing line from t2 to t4
/ \
/______\
t1\ /t3
\ /
\ /
\/
t2
four surface triangles t1 t2 t3, t1 t2 t4, t1 t3 t4, t2 t3 t4
The general volume computation:
of a closed surface is a little more complicated.
The sailors algorithm is still the basic idea.
Consider a closed surface covered by triangles. Each triangle is
three points and are coded counter clockwise such that the normal
vector to the triangle points out of the volume.
Make all z coordinates positive.
Compute the average z for a triangle, "height".
Compute the area for a triangle, "base".
Compute the z component of the normal vector, znorm.
The volume of this piece of the surface is
height times base times znorm
If znorm is positive, this triangle is on top and contributes
positive volume.
If znorm is negative, this triangle is on the bottom and
contributes negative volume.
The area in the x-y plane is the area of the triangle times znorm.
A vertical triangle has znorm = 0.
A horizontal triangle has znorm = 1 on top and -1 on bottom.
A triangle tipped 45 degrees has a znorm = cos(45 degrees) = 0.7071
znorm is computed using 3 or more points that lie in a plane,
x[0],y[0],z[0] x[1],y[1],z[1] x[2],y[2],z[2] forming
two vectors a and b, then computing the vector cross product:
float znormal(int n, float x[], float y[], float z[], float *area)
{
float ax, ay, az, bx, by, bz, nx, ny, nz, ss;
float cx, cy, cz, sss, sstot, ssstot;
int i;
sstot = 0.0;
ssstot = 0.0;
for(i=2; iNumerical approximation
Using Utah Graphics .dat file for input
volume_dat.py3 source code
volume_dat_py3_cubet.out
volume_dat_py3_tetra.out
tetra.dat input data
cubet.dat input data
A program that uses graphics data files to compute the volume and
area of a closed volume is:
volume_dat2.c
from data:
sphere_div.dat
output for a crude, 32 triangle, sphere is:
 volume_dat2.c reading sphere_div.dat
status=0, zmax=1, points=18, polys=32
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 10.4178, total volume = 2.94281
should be 12.56 and 4.189
from data:
sphere_div2.dat
output for a better, 128 triangle, sphere is:
volume_dat2.c reading sphere_div2.dat
status=0, zmax=1, points=66, polys=128
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 11.9549, total volume = 3.81773
should be 12.56 and 4.189
from data:
sphere_div3.dat
output for a better, 512 triangle, sphere is:
volume_dat2.c reading sphere_div3.dat
status=0, zmax=1, points=258, polys=512
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.4082, total volume = 4.0916
should be 12.56 and 4.189
from data:
sphere_div4.dat
output for a good, 2048 triangle, sphere is:
volume_dat2.c reading sphere_div.dat
status=0, zmax=1, points=18, polys=32
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 10.4178, total volume = 2.94281
should be 12.56 and 4.189
from data:
sphere_div2.dat
output for a better, 128 triangle, sphere is:
volume_dat2.c reading sphere_div2.dat
status=0, zmax=1, points=66, polys=128
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 11.9549, total volume = 3.81773
should be 12.56 and 4.189
from data:
sphere_div3.dat
output for a better, 512 triangle, sphere is:
volume_dat2.c reading sphere_div3.dat
status=0, zmax=1, points=258, polys=512
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.4082, total volume = 4.0916
should be 12.56 and 4.189
from data:
sphere_div4.dat
output for a good, 2048 triangle, sphere is:
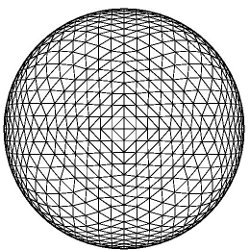 volume_dat2.c reading sphere_div4.dat
status=0, zmax=1, points=1026, polys=2048
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.5264, total volume = 4.16419
should be 12.56 and 4.189
The area of a perfect sphere of radius 1 is about 12.56
The volume of a perfect sphere of radius 1 is about 4.189
from data:
bball.dat Buckminster Fuller Geodesic
output for small, 90 triangle, sphere is:
volume_dat2.c reading sphere_div4.dat
status=0, zmax=1, points=1026, polys=2048
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.5264, total volume = 4.16419
should be 12.56 and 4.189
The area of a perfect sphere of radius 1 is about 12.56
The volume of a perfect sphere of radius 1 is about 4.189
from data:
bball.dat Buckminster Fuller Geodesic
output for small, 90 triangle, sphere is:
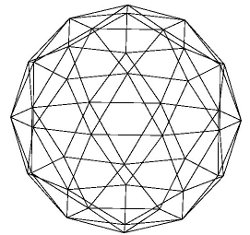 volume_dat2.c reading bball.dat
status=0, zmax=1, points=42, polys=90
xmin=-0.951060, xmax=0.951060, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 23.217, enclosing volume= 7.60848
final total area = 13.1894, total volume = 3.94159
should be 12.56 and 4.189
No bull? let us compute the volume of this bull
volume_dat2.c reading bball.dat
status=0, zmax=1, points=42, polys=90
xmin=-0.951060, xmax=0.951060, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 23.217, enclosing volume= 7.60848
final total area = 13.1894, total volume = 3.94159
should be 12.56 and 4.189
No bull? let us compute the volume of this bull
 datread.java needed for volume_dat2
volume_dat2.java program
bull.dat data
volume_dat2.c reading bull.dat
status=0, zmax=3177.82, points=6202, polys=12398
xmin=-2060.574463, xmax=1978.578857, ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
enclosing area= 6.40908e+07, enclosing volume= 3.43006e+10
final total area = 2.07025e+07, total volume = 3.64616e+09
That's a lot of bull!
Seems scaled up by 500 relative to feet, in all three dimensions.
Thus, about 29.16 cubic feet of bull.
datread.java needed for volume_dat2
volume_dat2.java program
bull.dat data
volume_dat2.c reading bull.dat
status=0, zmax=3177.82, points=6202, polys=12398
xmin=-2060.574463, xmax=1978.578857, ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
enclosing area= 6.40908e+07, enclosing volume= 3.43006e+10
final total area = 2.07025e+07, total volume = 3.64616e+09
That's a lot of bull!
Seems scaled up by 500 relative to feet, in all three dimensions.
Thus, about 29.16 cubic feet of bull.
 read_stl.java needed for volume_stl
volume_stl.java program
bull.stl data
volume_stl.c reading bull.stl
volume_stl reading file bull.stl
num_tri=12398
xmin=-2060.574463, xmax=1974.23877
ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
compute volume and area
final total area =2.0702515385253366E7, total volume =3.646510695181979E9
read_stl.java needed for volume_stl
volume_stl.java program
bull.stl data
volume_stl.c reading bull.stl
volume_stl reading file bull.stl
num_tri=12398
xmin=-2060.574463, xmax=1974.23877
ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
compute volume and area
final total area =2.0702515385253366E7, total volume =3.646510695181979E9
Changing volume_dat2.c to volume_ucd.c
Just reading a UCD .inp file, rather than a .dat file.
volume_ucd.c
blivet.inp
volume_ucd_c.out

determining surface normal vectors
The blue dot is on the surface, the red dot is the
direction of the normal.
normal_dat.c
blivet.dat
star3.dat
star3tri.dat
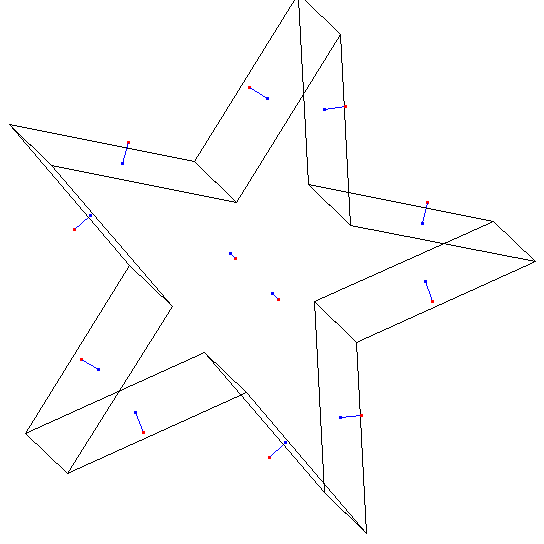
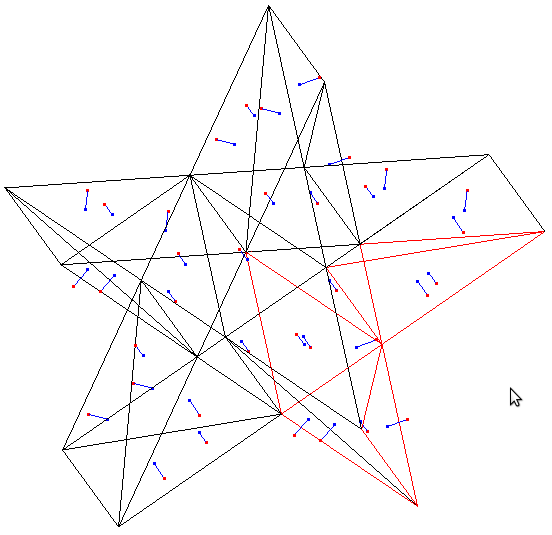 volume_dat2_star3tri.out
volume_dat2_star3tri.out
More than you every wanted to know about cross product
For 3, 4, 5 etc. dimensions the cross product is a vector in
that dimension that is orthogonal to the given d-1 vectors
in that dimension. The comments, many lines, in the following "C"
program provide definitions, then code provides demonstration.
The checking is that the dot product of two orthogonal vectors
is zero.
cross_general.c comments and source
cross_general_c.out output
cross_general.java comments and source
cross_general_java.out output
simeq_plus.c utility
simeq_plus.h utility
Then, bland 3D versions.
cross_product.c comments and source
cross_product_c.out output
simeq_plus.c utility
simeq_plus.h utility
Then, 6D version, not unique, choice of fill.
cross_product6d.c comments and source
cross_product6d_c.out output
determinant.c utility
determinant.h utility
Then, 6D version, not unique, unit vector fill when less than 5 given.
cross_product6du.c comments and source
cross_product6du_c.out output
determinant.c utility
determinant.h utility
Then there are ellipse, development test to get to ellipse3:
ellipse.java source code
 ellipse.java source code
ellipse.java source code
ellipse.java source code
ellipse_java.out output
ellipse.java source code
ellipse.java source code
ellipse.java source code
ellipse_java.out output
 To determine if a point x,y is inside a closed polygon of lines
test_inside.java source code
test_inside_java.out output
test_meet.java source code
test_meet_java.out output
For sharpening your observation, analyze a few optical illusions:
www.pcmag.com/slideshow/story/325796/14-optical-illusions-that-prove-your-brain-sucks
To determine if a point x,y is inside a closed polygon of lines
test_inside.java source code
test_inside_java.out output
test_meet.java source code
test_meet_java.out output
For sharpening your observation, analyze a few optical illusions:
www.pcmag.com/slideshow/story/325796/14-optical-illusions-that-prove-your-brain-sucks
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation
 The intuition for the Sailors Algorithm, on a shape with only
vertical and horizontal edges is:
a vertical line adds no area
a horizontal line to the right adds area (length times average height)
a horizontal line to the left subtracts area.
The computed area will be positive if an upper outside edge is
listed in counter clockwise order, else negative, take absolute value.
A sample program is:
area2_dat.py3 source code
star.dat input
area2_dat_py3.out output
poly_area.c
poly_area_maze.out
maze.path
poly_area_star.out
star.path
sailors_area.java
sailors_area_java.out
The maze (8 units wide, 7 units high, area is 35) is:
The intuition for the Sailors Algorithm, on a shape with only
vertical and horizontal edges is:
a vertical line adds no area
a horizontal line to the right adds area (length times average height)
a horizontal line to the left subtracts area.
The computed area will be positive if an upper outside edge is
listed in counter clockwise order, else negative, take absolute value.
A sample program is:
area2_dat.py3 source code
star.dat input
area2_dat_py3.out output
poly_area.c
poly_area_maze.out
maze.path
poly_area_star.out
star.path
sailors_area.java
sailors_area_java.out
The maze (8 units wide, 7 units high, area is 35) is:
 The star (inscribed in a circle with radius 5, area about 28.06) is:
The star (inscribed in a circle with radius 5, area about 28.06) is:
 Volume of a sphere 4/3 Pi r^3
Area of a sphere 4 Pi r^2
Volume of a cone, tetrahedron, any solid with a planar base that goes
to a point 1/3 base area times height
| 1 x1 y1 z1 |
Volume of a tetrahedron 1/6 det | 1 x2 y2 z2 |
| 1 x3 y3 z3 |
| 1 x4 y4 z4 |
using just the x,y,z of the four vertices t1, t2, t3, t4
t4
/\
/ \ missing line from t2 to t4
/ \
/______\
t1\ /t3
\ /
\ /
\/
t2
four surface triangles t1 t2 t3, t1 t2 t4, t1 t3 t4, t2 t3 t4
Volume of a sphere 4/3 Pi r^3
Area of a sphere 4 Pi r^2
Volume of a cone, tetrahedron, any solid with a planar base that goes
to a point 1/3 base area times height
| 1 x1 y1 z1 |
Volume of a tetrahedron 1/6 det | 1 x2 y2 z2 |
| 1 x3 y3 z3 |
| 1 x4 y4 z4 |
using just the x,y,z of the four vertices t1, t2, t3, t4
t4
/\
/ \ missing line from t2 to t4
/ \
/______\
t1\ /t3
\ /
\ /
\/
t2
four surface triangles t1 t2 t3, t1 t2 t4, t1 t3 t4, t2 t3 t4
 volume_dat2.c reading sphere_div.dat
status=0, zmax=1, points=18, polys=32
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 10.4178, total volume = 2.94281
should be 12.56 and 4.189
from data:
sphere_div2.dat
output for a better, 128 triangle, sphere is:
volume_dat2.c reading sphere_div2.dat
status=0, zmax=1, points=66, polys=128
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 11.9549, total volume = 3.81773
should be 12.56 and 4.189
from data:
sphere_div3.dat
output for a better, 512 triangle, sphere is:
volume_dat2.c reading sphere_div3.dat
status=0, zmax=1, points=258, polys=512
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.4082, total volume = 4.0916
should be 12.56 and 4.189
from data:
sphere_div4.dat
output for a good, 2048 triangle, sphere is:
volume_dat2.c reading sphere_div.dat
status=0, zmax=1, points=18, polys=32
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 10.4178, total volume = 2.94281
should be 12.56 and 4.189
from data:
sphere_div2.dat
output for a better, 128 triangle, sphere is:
volume_dat2.c reading sphere_div2.dat
status=0, zmax=1, points=66, polys=128
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 11.9549, total volume = 3.81773
should be 12.56 and 4.189
from data:
sphere_div3.dat
output for a better, 512 triangle, sphere is:
volume_dat2.c reading sphere_div3.dat
status=0, zmax=1, points=258, polys=512
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.4082, total volume = 4.0916
should be 12.56 and 4.189
from data:
sphere_div4.dat
output for a good, 2048 triangle, sphere is:
 volume_dat2.c reading sphere_div4.dat
status=0, zmax=1, points=1026, polys=2048
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.5264, total volume = 4.16419
should be 12.56 and 4.189
The area of a perfect sphere of radius 1 is about 12.56
The volume of a perfect sphere of radius 1 is about 4.189
from data:
bball.dat Buckminster Fuller Geodesic
output for small, 90 triangle, sphere is:
volume_dat2.c reading sphere_div4.dat
status=0, zmax=1, points=1026, polys=2048
xmin=-1.000000, xmax=1.000000, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 24, enclosing volume= 8
final total area = 12.5264, total volume = 4.16419
should be 12.56 and 4.189
The area of a perfect sphere of radius 1 is about 12.56
The volume of a perfect sphere of radius 1 is about 4.189
from data:
bball.dat Buckminster Fuller Geodesic
output for small, 90 triangle, sphere is:
 volume_dat2.c reading bball.dat
status=0, zmax=1, points=42, polys=90
xmin=-0.951060, xmax=0.951060, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 23.217, enclosing volume= 7.60848
final total area = 13.1894, total volume = 3.94159
should be 12.56 and 4.189
No bull? let us compute the volume of this bull
volume_dat2.c reading bball.dat
status=0, zmax=1, points=42, polys=90
xmin=-0.951060, xmax=0.951060, ymin=-1.000000, ymax=1.000000
zmin=-1.000000, zmax=1.000000
enclosing area= 23.217, enclosing volume= 7.60848
final total area = 13.1894, total volume = 3.94159
should be 12.56 and 4.189
No bull? let us compute the volume of this bull
 datread.java needed for volume_dat2
volume_dat2.java program
bull.dat data
volume_dat2.c reading bull.dat
status=0, zmax=3177.82, points=6202, polys=12398
xmin=-2060.574463, xmax=1978.578857, ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
enclosing area= 6.40908e+07, enclosing volume= 3.43006e+10
final total area = 2.07025e+07, total volume = 3.64616e+09
That's a lot of bull!
Seems scaled up by 500 relative to feet, in all three dimensions.
Thus, about 29.16 cubic feet of bull.
datread.java needed for volume_dat2
volume_dat2.java program
bull.dat data
volume_dat2.c reading bull.dat
status=0, zmax=3177.82, points=6202, polys=12398
xmin=-2060.574463, xmax=1978.578857, ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
enclosing area= 6.40908e+07, enclosing volume= 3.43006e+10
final total area = 2.07025e+07, total volume = 3.64616e+09
That's a lot of bull!
Seems scaled up by 500 relative to feet, in all three dimensions.
Thus, about 29.16 cubic feet of bull.
 read_stl.java needed for volume_stl
volume_stl.java program
bull.stl data
volume_stl.c reading bull.stl
volume_stl reading file bull.stl
num_tri=12398
xmin=-2060.574463, xmax=1974.23877
ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
compute volume and area
final total area =2.0702515385253366E7, total volume =3.646510695181979E9
read_stl.java needed for volume_stl
volume_stl.java program
bull.stl data
volume_stl.c reading bull.stl
volume_stl reading file bull.stl
num_tri=12398
xmin=-2060.574463, xmax=1974.23877
ymin=-1580.072998, ymax=1429.878052
zmin=356.500702, zmax=3177.816406
compute volume and area
final total area =2.0702515385253366E7, total volume =3.646510695181979E9


 volume_dat2_star3tri.out
volume_dat2_star3tri.out
 ellipse.java source code
ellipse.java source code
ellipse.java source code
ellipse_java.out output
ellipse.java source code
ellipse.java source code
ellipse.java source code
ellipse_java.out output
 To determine if a point x,y is inside a closed polygon of lines
test_inside.java source code
test_inside_java.out output
test_meet.java source code
test_meet_java.out output
For sharpening your observation, analyze a few optical illusions:
www.pcmag.com/slideshow/story/325796/14-optical-illusions-that-prove-your-brain-sucks
To determine if a point x,y is inside a closed polygon of lines
test_inside.java source code
test_inside_java.out output
test_meet.java source code
test_meet_java.out output
For sharpening your observation, analyze a few optical illusions:
www.pcmag.com/slideshow/story/325796/14-optical-illusions-that-prove-your-brain-sucks