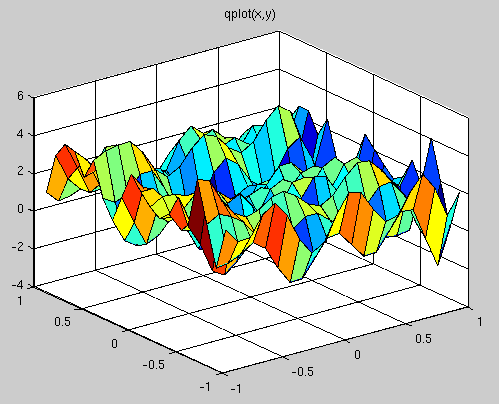
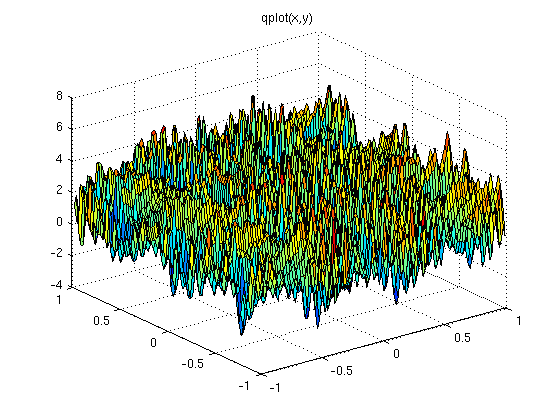
A smaller dx,dy plot
"see lecture 15 for multiple precision"
"see lecture 17 for optimization"
Python mpmath use mpf.dps = 200 # computation precision
mp.dps = 100 # print precision
Everything due 12/20
[CMSC 455] | [Syllabus] | [Lecture Notes] | [Homework] | [Projects] | [Files] | [Notes, all]
Do not talk to other students about the project.
You may use gmp, BigDecimal, apfloat, mpmath, MatLab, Maple,
Mathematica or other existing software, and any software from
the course WEB site. (Slightly different from previous semesters.)
Given the equation: (different each semester)
z = exp(sin(50.0*x)) + sin(60.0*exp(y)) +
sin(70.0*sin(x)) + sin(sin(80.0*y)) -
sin(10.0*(x+y)) + (x*x+y*y)/4.0
Find the global minimum z in -1 < x < 1 , -1 < y < 1
Step size dx = 0.001 dy = 0.001 yes 4 million test.
Print x, y, z at end of file.
Your z should be < -3.306 at x = -0.024 y = 0.210
Better step size dx = 0.0001 dy = 0.0001 with
xmin = -0.1 xmax=0.0 ymin = 0.2 ymax 0.3 only 1 million test.
Use just normal programming, too slow to do this in multiple precision.
OK to turn in paper or submit global search and code to minimize
single precision and to minimize multiple precision, as seperate files.
Check your code, be near x = -0.0244, y = 0.2106, z = -3.306868
Then put best global minimum into multiple precision in some language.
From my download directory, sample code:
for C, mpf_math.h mpf_sin_cos.c mpf_exp.c and supporting code
Also, for Java, Big_math.java and test_Big_math.java.
and test_apfloat.java
Also, for Python, test_mpmath.py3 need python 3 on linux.gl
There are many local minima, do not get stuck in one of them.
A global search with dx and dy <= 0.001 should be in the
global minimum. Do global search in only double precision.
From the global search starting point, use optimization.
More points if multiple precision is used in this part.
Typically 120 digits about 380 bits.
See lecture 17, optmn samples and spiral examples.
Or:
Optimization for finding x,y of smallest z(x,y)
X
| x-dx,y+dy x,y+dy x+dx,y+dy
| o o o
|
| x-dx,y x,y x+dx,y
| o o o
|
| x-dx,y-dy x,y-dy x+dx,y-dy
| o o o
|
--------+------------------------------------------------ Y
|
| You are at minimum, from global search, z(x,y)
| Check z at 8 points shown above, around x,y
| If any z(point) < z(x,y) move x,y to minimum point
| Else move to ((x,y) + (minimum point))/2 decrease dx,dy, or both
| Keep repeating until no progress, you are at smallest dx,dy
Do not allow dx, dy to get too small, roundoff error if less than
1.0E-16 in 64 bit floating point
1.0E-100 in multiple precision
Here is optm algorithm: check 8 points around x,y of global search
then keep running with new values shown below.
First dx, dy values are one half last dx,dy used in global search.
if best if best if besy
f(x-dx, y+dy) f(x, y+dy) f(x+dx, y+dy)
x = x-dx x = x no change x = x+dx
y = y+dy y = y+dy y = y+dy
dx = dx/2 dy = dy/2 dx = dx/2
dy = dy/2 dy = dy/2
if best if best if best
f(x-dy,y) f(x,y) f(x+dx,y)
x = x-dx dx = dx/2 x=x+dx
y = y dy = dy/2 dx = dx/2
dx = dx/2
if best if best if best
f(x-dx),y-dy) f(x,y-dy) f(x+dx,y-dy)
x = x-dx x = x no change x = x+dx
y = y-dy y = y-dy y = y-dy
dx = dx/2 dx no change dx = dx/2
dy = dy/2 dy = dy/2 dy = dy/2
obviously z is best z of 8 function evaluations, else no change in x,y
if none of 8 have smaller z, then dx = dx/2 dy=dy/2 keep going
keep going until dx < 1.0e-100 and dy < 1.0e-100
Print your x and y and z.
I would expect, all to the same number of digits accuracy. (not just %f)
Your points are based on the accuracy of your computed
"x", "y", "z".
Your largest error in x, y, or z rounded to significant digits:
2 digits 50 points
3 digits 60 points
4 digits 70 points
5 digits 74 points
6 digits 78 points
7 digits 80 points
8 digits 82 points
9 digits 83 points
10 digits 84 points
11 digits 85 points
12 digits 86 points
13 digits 87 points
14 digits 88 points
15 digits 89 points
16 digits 90 points
20 digits 91 points
30 digits 92 points
40 digits 93 points
50 digits 94 points
60 digits 95 points
70 digits 96 points
90 digits 99 points
100 digits 100 points
The project source and output can be turned in on paper or may be submitted on GL as submit cs455 proj list-of-source-files text_output-file one file should be your text output file The list-of-files should include source code and output and other files that were used. Do not turn in or submit executable file(s). Use a language of your choice on an operating system of your choice, unless otherwise stated. Talk to the instructor if your language choice is not one of: Ada 95, C, C++, Fortran 95, Java, Python, Scala, SML, MATLAB, Maple, Mathematica, or similar available language or product. The goal of the project is to give you a useful numeric code that you can apply as needed to future tasks. This includes converting a working numeric code to your language of choice or being able to interface some working numeric code with your language of choice. Copying of a project results is zero points for everyone involved in copying. Be sure to check your own answers by using several languages or several implementations. You may want to do the global search in a language that is fast, tuen in paper or submit that code, and then start the multiple precision at the x,y found in the global search with a small dx,dy. A crude plot of similar equation z vs x,y is
Last updated 12/19/2021