<- previous    index    next ->

Lecture 22, Project Discussion 


Project writeup
 
Use a plotting utility to look at the shape of the function. sample shown

Do a global global search to find candidate staring point, first xbest,ybest.
-1.0 < x < 1.0   -1.0 < y < 1.0    for this project
You need dx, dy of 0.001 to get you into the global minima well.
The global minimum value must be between -3 and -4 by analysis of equation.
You saved best as xbest, ybest, zbest. OK to print.

Top view   f(x-dx,y+dy)   f(x,y+dy)   f(x+dx,y+dy)    x is xbest, y is ybest
           f(x-dx,y)      f(x,y)      f(x+dx,y)       f(x,y) smallest yet
           f(x-dx,y-dy)   f(x,y-dy)   f(x+dx,y-dy)

Refine from your search result to get a set of eight surrounding
values greater or lower than the zbest value found
refine dx and dy, dx = dx/2,  dy=dy/2

example:
                                 *             
                 *               |        
                 |               |     *                  *
                 |     *         |     |           *      |
           *     |     |         |     |           |      |
           |     |     |    0    |     |           |  (x+dx,y+dy)
           |     |     |    |    |     |     *     |
           |     |     |  (x,y)  |     |     | (x+dx,y-dy)
           |     |     |         |     |     | 
     (x-dx,y-dy) | (x,y-dy)   (x,y+dy) | (x-dx,y+dy)
                 |                     |
             (x-dx,y)               (x+dx,y)



If none of the 8 z's are smaller, xbest and ybest do not change.
dx = dx/2, dy= dy/2,  quit if dx and dy are smaller than desired accuracy.
Use smallest of 8 and adjust  xbest,ybest to midpoint between old x,y and
best (x+/-dy, y+/-dy)  8 possible cases.
e.g.  (x-dx,y+dy) was smallest:
                                xbest = xbest-dx
                                dx = dx/2
                                ybest = ybest+dy
                                dy = dy/2

It is OK to print and see progress, typically not at every step.

Or, given a good candidate staring point, use an available minimization
code, typically name  "optm"  is in file name.

Or, use the previously described expanding and contracting search
that used pseudo derivatives,Lecture 17.

To get high accuracy, 100 digits, requires that the function be
evaluated using multiple precision, covered in an earlier lecture.

Typically, if 100 digit accuracy is desired, then all computation
would be performed at 110 to 200 digit accuracy. This is slow yet
not difficult for sin(x) and exp(x) for small values of x.

exp(x)=1 + x + x^2/2! + x^3/3! + x^4/4! + ...
For |x|<1 you need the nth term where n! > 10^110 or n=75

Or, you can use range reduction and a much shorter series
normalize and use series
e^x = e^j * e^xc   integer j, xc = x-j
if xc<1/4 series(xc), if xc<1/2 series(xc/2)^2, else series(xc/4)^4
series  1 + x + x^2/2! + x^3/3! + ... be sure to use multiple precision


Similarly for sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...
Similarly for cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
For sqrt(x) make a guess y=1, then iterate y=(y+x/2)/2
until |y-y_previous| < 10^110

Actually, not quite that easy. You must use range reduction
to get |x|<1 and better if |x| < 1/2.
e.g.  for sin(x): if abs(x)>2Π then x=x rem 2Π
                  if x>Π then x=x-2Π
                  if x<Π then x=x+2Π
                  if x>Π/2 then x=Π-x
                  if x<Π/2  then x=Π+x  now abs(x)<Π/2 1.57
                  use sin(x)=2 sin(x/2) cos(x/2) on x/2<Π/4  0.78

Several of the implementations to 200 digits, that I have programmed:
generic_digits_arithmetic.adb
mpf_sin_cos.c
mpf_exp.c
mpf_exp.h
mpf_base.c
mpf_math.h
Big_math.java
test_Big_math.java
Makefile_proj



Obviously, you find a good staring point with global search
using only double precision and
then use a reasonable optimization method to get a good
starting  x,y  before going to multiple precision computation.

Print, at least the first few, multiple precision values of
x, y, and function and compare to your code that used
double precision floating point. C, Java, Python, Matlab, etc.

Here is why you must do a global search:



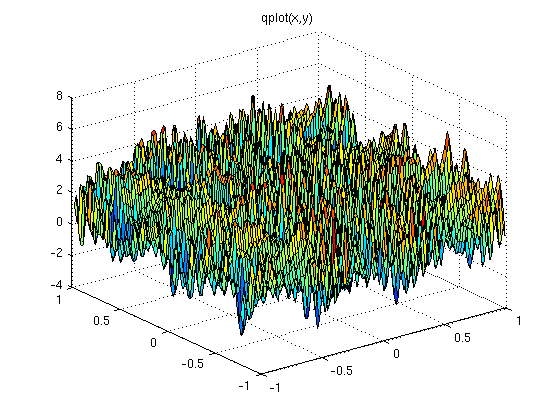z = exp(sin(50.0*x)) + sin(60.0*exp(y)) +
    sin(70.0*sin(x)) + sin(sin(80.0*y)) -
    sin(10.0*(x+y)) + (x*x+y*y)/4.0

check you equation when doing project:
for  x = -0.0245  y = 0.2105  z should be close to = -3.3067


z = f(x,y)  typically set x = xbest, y= ybest, then (x+dx,y) etc.
                          save z, then  zbest = z


When using java, you may need many compilations:
optmn_run.make

Project writeup


Another problem that requires minimation needs physics:
space satellite problem

One possible simple solution:
satellite.java source code
satellite_java.out solution
satellite.py3 source code
satellite_py3.out solution
Could get closer, not needed for launch of satellite.

The function to find the minimum changes every semester.
See project page for this semesters f(x,y)


    <- previous    index    next ->

Other links

Go to top