<- previous    index    next ->

Lecture 21, Benchmarks, time and size 

A computer benchmark will typically be some code that is executed
and the running time measured. 

A few simple rules about benchmarks:

1) Do not believe or trust any person, any company, any data.

2) Expect the same code to give different times on:
   different operating systems,
   different compilers,
   different computers from various manufacturers
             (IBM, Sun, Intel, AMD) even at same clock speed,
             (IBM Power fastest, AMD next fastest with same memory, cache)
   different languages, even for line by line translation.

3) If you want to measure optimization, turn it on,
   otherwise prevent all optimization.
             (Most compilers provide optimization choices)
             (Add code to prevent inlining of functions, force store)

4) You will probably be using your computers clock to measure time.
   Test that the clock is giving valid results for the language
   you are using. The constant CLOCKS_PER_SEC in the "C" header
   file  time.h  has been found to be wrong.
   One manufacturer put a capacitor across the clock circuitry
   on a motherboard and all time measurements were half the
   correct time. See sample test below.

5) For measuring short times you will need to use the
   "double difference method". This method can be used to
   measure the time of a single instruction. This method
   should be used for any benchmark where one iteration of
   the code runs in less than a second. See sample test below.

6) Some methods of measuring time on a computer are only
   accurate to one second. Generally run enough iterations of
   your code in loops to get a ten second measurement.
   Some computers provide a real time clock as accurate as
   one microsecond, others one millisecond and some poorer than
   a fiftieth of a second.

7) Turn off all networking and stop all software that might run
   periodically. If possible, run in single user mode. You want to
   measure your code, not a virus checker or operating system.
   I once did measurement on a Sun computer running Solaris. It 
   seemed to slow down periodically. I found that the operating
   system periodically checked to see if any disk files needed
   to be written.

8) If you are interested in how fast your application might run
   on a new computer, find reputable benchmarks that are for
   similar applications. I do a lot of numerical computation, thus
   all my benchmarks are heavily floating point. You may be
   more interested in disk performance or network performance.

9) Do not run all all zero data. Some compilers and very smart and
   may precompute your result without running you code.
   Be sure to use every result. Compilers do "dead code elimination"
   that checks for code where the results are not used and just
   does not produce instructions for that "dead code." An "if" test
   or printing out the result is typically sufficient. For vectors
   and arrays, usually printing out one element is sufficient.

10) It helps to be paranoid. Check that you get the same results
    by running n iterations, then 2n iterations. If the time did
    not double, you do not have a stable measurement. Run 4n and 8n
    and check again. It may not be your benchmark code, it may be
    an operating system activity.

11) Do not run a benchmark across midnight. Most computers reset
    the seconds to zero at midnight.

12) Keep values of time as a double precision numbers.

13) Given an algorithm where you can predict the time increase
    as the size of data increases: e.g. FFT is order  n log2 n,
    multiplying a matrix by a matrix is order n^3, expect
    non uniform results for some values of n.

    Consider the case where all your code and all your data fit
    in the level one caches. This will be the fastest.

    Consider when you data is much larger than the level one cache
    yet fits in the level two cache. You are now measuring the
    performance of the level two cache.

    Consider when your data fits in RAM but is much larger than
    your level two (or three) cache. You are now measuring the speed
    of your code running in RAM.

    Consider when your data is much larger than your RAM, you are
    now running in virtual memory from your disk drive. This will
    be very slow and you are measuring disk performance.




In order to check the hardware and software time from your computers
clock, run the following two programs. Translate to the language
of your choice. The concept is to have the program display the number
of seconds every 5 seconds for a minute and a half. You check
the display against a watch with a second hand.

The first code uses "clock()" for process time and the second code
uses "time()" for wall clock time.


 /* time_cpu.c    see if  C  time.h   clock() is OK */
 /*               in theory, this should be only your processes time */
 #include <stdio.h>
 #include <time.h>
 int main()
 {
   int i;
   double now;
   double next;

   printf("Should be wall time, 5 second intervals \n");
   now = (double)clock()/(double)CLOCKS_PER_SEC;
   next = now+5.0;

   for(i=0; i<90;)
   {
     now = (double)clock()/(double)CLOCKS_PER_SEC;
     if(now >= next) 
     {
       printf("%d\n",i);
       i=i+5;
       next=next+5.0;
     }    
   } 
   return 0;
 }
            (If time_cpu runs slow, your process is being interrupted.)
            time_cpu_c.out



 /* time_test.c    see if  C  time.h   time(NULL) is OK */
 #include <stdio.h>
 #include <time.h>
 int main()
 {

   int i;
   double now;
   double next;

   printf("Should be wall time, 5 second intervals \n");
   now = (double)time(NULL);
   next = now+5.0;

   for(i=0; i<90;)
   {
     now = (double)time(NULL);
     if(now >= next) 
     {
       printf("%d\n",i);
       i=i+5;
       next=next+5.0;
     }    
   } 
   return 0;
 }
                     time_test_c.out


The "Double Difference Method" tries to get accurate measurement
for very small times. The code to time a single floating point
add instruction is shown below. The principal is:

  measure time, t1

  run a test harness with loops that has everything except the code
  that you want to time. Count the number of executions as a check.

  measure time, t2

  measure time, t3

  run exactly the same code from the test harness with only the
  feature you want to measure added. Count number of executions.

  measure time, t4

  check that the number of executions is the same.
  check that  t2-t1 was more than 10 seconds

  the time for the feature you wanted to measure is

  t5 = ((t4 - t3) - (t2 - t1))/ number of executions

  basically measured time minus test harness time divided by the
  number of executions.

 /* time_fadd.c  try to measure time of double  A = A + B;         */
 /*              roughly time of one floating point add            */
 /*              using double difference and minimum and stability */

 #include <time.h>
 #include <stdio.h>
 #include <math.h>

 #define dabs(a) ((a)<0.0?(-(a)):(a))
 void do_count(int * count_check, int rep, double * B);

 int main(int argc, char * argv[])
 {
   double t1, t2, t3, t4, tmeas, t_min, t_prev, ts, tavg;
   double A, B, Q;
   int stable;
   int i, j;
   int count_check, outer;
   int rep, min_rep;


   t_min = 10.0;    /* 10.0 seconds typical minimum measurement time */
   Q  = 5.0;        /* 5.0 typical approximate percentage stability */
   min_rep = 32;    /* minimum of 32 typical */
   outer = 100000;  /* some big number */

   printf("time_fadd.c \n");
   printf("min time %g seconds, min stability %g percent, outer loop=%d\n",
          t_min, Q, outer);


   stable = 5; /* max tries */
   t_prev = 0.0;
   for(rep=min_rep; rep<100000; rep=rep+rep) /* increase until good measure */
   {
     A = 0.0;
     B = 0.1;
     t1 = (double)clock()/(double)CLOCKS_PER_SEC;
     for(i=0; i<outer; i++) /* outer control loop */
     {
       count_check = 0;
       for(j=0; j<rep; j++)   /* inner control loop */
       {
          do_count(&count_check, rep, &B);
       }
     }
     t2 = (double)clock()/(double)CLOCKS_PER_SEC;
     if(count_check != rep) printf("bad count_check_1 %d \n", count_check);

     A = 0.0;
     t3 = (double)clock()/(double)CLOCKS_PER_SEC;
     for(i=0; i<outer; i++) /* outer measurement loop */
     {
       count_check = 0;
       for(j=0; j<rep; j++)   /* inner measurement loop */
       {
         do_count(&count_check, rep, &B);
         A = A + B;   /* item being measured, approximately FADD time */
       }
     }
     t4 = (double)clock()/(double)CLOCKS_PER_SEC;
     if(count_check != rep) printf("bad count_check_2 %d \n", count_check);

     tmeas = (t4-t3) - (t2-t1); /* the double difference */
     printf("rep=%d, t measured=%g \n", rep, tmeas);

     if((t4-t3)<t_min) continue; /* need more rep */

     if(t_prev==0.0)
     {
       printf("tmeas=%g, t_prev=%g, rep=%d \n", tmeas, t_prev, rep);
       t_prev = tmeas;
     } 
     else /* compare to previous */
     {
       printf("tmeas=%g, t_prev=%g, rep=%d \n", tmeas, t_prev, rep);
       ts = 2.0*(dabs(tmeas-t_prev)/(tmeas+t_prev));
       tavg = 0.5*(tmeas+t_prev);
       if(100.0*ts < Q)  break; /* above minimum and stable */
       t_prev = tmeas;
     }
     stable--;
     if(stable==0) break;
     rep = rep/2; /* hold rep constant */
   } /* end loop increasing rep */

   /* stable? and over minimum */
   if(stable==0) printf("rep=%d  unstable \n", rep);
   if(tmeas<t_min) printf("time measured=%g, under minimum \n", tmeas);
   printf("raw time=%g, fadd time=%g, rep=%d, stable=%g\% \n\n", tmeas, 
          (tavg/(double)outer)/(double)rep, rep, ts);
   return 0;
 } /* end time_fadd.c */

 /* do_count to prevent dead code elimination  */
 void do_count(int * count_check, int rep, double * B)
 {
   (*count_check)++;
   /* could change B but probably don't have to. */
 }

time_fadd_sgi.out
time_fadd_c_sun.out
time_fadd_c_mac.out



You might think that I am obsessed with time. :)

time_cpu.c
time_cpu_c.out
timet_cpu.py3
timet_cpu_py3.out
time_cpu.py3 test
time_test.c
time_test_c.out
time_mp2.c
time_mp2_c.out
time_mp4.c
time_mp4_c.out
time_mp8.c
time_mp8_c.out
time_mp12.c
time_mp12_c.out
time_mp12.c
time_mp12_c.out
time_mp12.c
time_mp12_c.out
time_mp12.c
time_mp12_c.out
time_mp12.c
time_mp12_c.out
fft_time.c
fft_time_a533.out

time_mp2.java
time_mp2_java.out
time_mp4.java
time_mp4_java.out
time_mp8.java
time_mp8_java.out
time_mp12_12.java
time_mp12_12_java.out
time_mp16.java
time_mp16a_java.out
time_mp32.java
time_mp32_java.out
time_mp32a.java
time_mp32a_java.out
time_simeq_thread.java
time_simeq_thread_java.out
time_of_day.java
time_of_day.out

time_cpu.py  # python3
time_cpu_py.out
time_test.py
time_test_py.out
time_thread.py
time_thread_py.out
time_cpu.py3
time_cpu_py3.out
time_fadd.py3
time_fadd_py3.out
time_matmul.py3
time_matmul_py3.out
time_matmuln.py3 using numpy
time_matmuln_py3.out

time_test.f90

Many WEB site download/upload speed tests, search or try one:
 just click either speed test



64 bit computer architecture

If you have a 64-bit computer and more than 4GB of RAM, here is a
test you may want to run in order to check that your operating
system and compiler are both 64-bit capable:

big_malloc.c

big_malloc.c running, 10 malloc and free 1GB 
about to malloc and free 1GB the 1 time 
about to malloc and free 1GB the 2 time 
about to malloc and free 1GB the 3 time 
about to malloc and free 1GB the 4 time 
about to malloc and free 1GB the 5 time 
about to malloc and free 1GB the 6 time 
about to malloc and free 1GB the 7 time 
about to malloc and free 1GB the 8 time 
about to malloc and free 1GB the 9 time 
about to malloc and free 1GB the 10 time 
about to malloc and free 2000000000 
about to malloc and free 3000000000 
about to malloc and free 4000000000 
about to malloc and free 5000000000 
about to malloc and free 6000000000 
about to malloc and free 7000000000 
try calloc on 800000000 items of size 8 6.4GB 
successful end big_malloc 

A 28,000 by 28,000 matrix of double requires about 6.4GB of RAM.

In general, 64-bit is currently supported for the "C" type long
rather than int. Hopefully this will change as most desktop and
laptop computers become 64-bit capable. A small test of various
types and the size in bytes of the types and objects of various
types is:

big.c and its output (older OS)

big.c  compiled  gcc -m64 -o big big.c (64 bit long)
sizeof(int)=4, sizeof(int1)=4 
sizeof(long)=8, sizeof(long1)=8 
sizeof(long long)=8, sizeof(llong1)=8 
sizeof(float)=4, sizeof(fl1)=4 
sizeof(double)=8, sizeof(d1)=8 
sizeof(size_t)=8, sizeof(sz1)=8 
sizeof(int *)=8, sizeof(p1)=8 
n factorial with n of type long 
0 ! = 1 
1 ! = 1 
2 ! = 2 
3 ! = 6 
4 ! = 24 
5 ! = 120 
6 ! = 720 
7 ! = 5040 
8 ! = 40320 
9 ! = 362880 
10 ! = 3628800 
11 ! = 39916800 
12 ! = 479001600 
13 ! = 6227020800 
14 ! = 87178291200 
15 ! = 1307674368000 
16 ! = 20922789888000 
17 ! = 355687428096000 
18 ! = 6402373705728000 
19 ! = 121645100408832000 
20 ! = 2432902008176640000 
21 ! = -4249290049419214848     BAD!
22 ! = -1250660718674968576 
23 ! = 8128291617894825984 
24 ! = -7835185981329244160 



big12.c and its output (newer OS)
Note: 'sizeof' change to long, needs %ld rather than %d

big12.c  compiled  gcc -o big12 big12.c (64 bit long)
-m64 needed on some older OS 
sizeof(sizeof(int))=8, sizeof needs pct ld 
sizeof(int)=4, sizeof(int1)=4 
sizeof(long)=8, sizeof(long1)=8 
sizeof(long long)=8, sizeof(llong1)=8 
sizeof(float)=4, sizeof(fl1)=4 
sizeof(double)=8, sizeof(d1)=8 
sizeof(size_t)=8, sizeof(sz1)=8 
sizeof(int *)=8, sizeof(p1)=8 
n factorial with n of type long (same) 
...
trying to malloc 10GB 
malloc returned 
stored 10GB of 'a' 


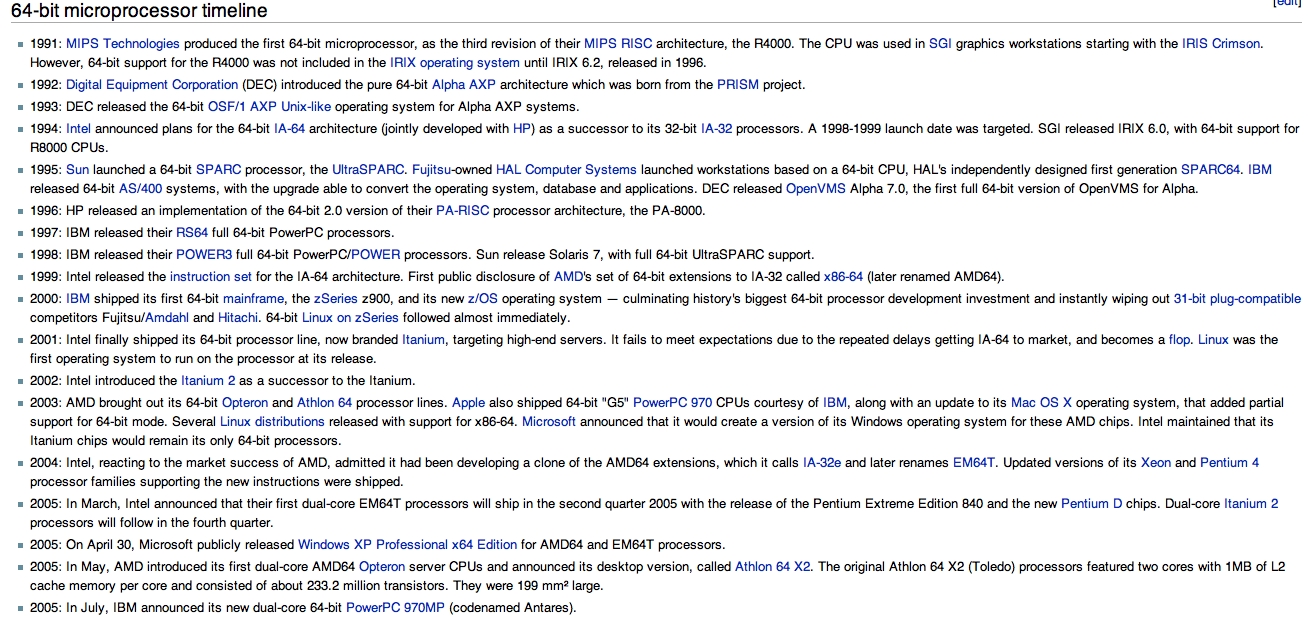
Some information on the long history of 64-bit computers:



Other code to find out how big an array can be in your
favorite language on your computer:

big_mem.f90 and its output
big_mem.java and its output
big_mem.c and its output
big_mem.adb and its output
Then, more like big_malloc.c, Ada "new"
source code big_new.adb
output from a PC big_new_ada.out
output from a MAC big_new_mac.out
output from a AMD big_new_amd.out
Yes, 50,000 by 50,000 8-byte floating point, not sparse.
20GB of RAM in one matrix.

Now do HW6


    <- previous    index    next ->

Other links

Go to top