<- previous index next ->
Serial bus, some were 9 pin, some were 15 pin, replaced by USB.
A modem modulator-demodulator was used to have computer access to
remote places over phone lines. Some initially called blackboards,
befor the Internet. Modems use serial bit two way transmission.
The serial bus went through many speed increases shown with
approximate dates in the following table:
approx speed used by me
date
1958 110 baud
1962 300 baud hand set phone
1972 1200 baud plug into phone line
2400 baud
4800 baud
9600 baud hard wired to computer to display
1991 14.400 baud called 14 dot 4 kilobaud not used
28.800 baud
1998 33.600 baud
Along the way there were many standards V.32 V.42 V.70 etc.
Bits were sent serially, start-bit, b1 b2 b3 b4 b5 b6 b7 b8 parity stop-bit
11 bits per byte. Thus 110 baud sent 10 bytes per second.
No problem for keyboard typing, slow for display. UART does control.
some review:
A Karnaugh map, K-map, is a visual representation of a Boolean function.
The plan is to recognize patterns in the visual representation and
thus find a minimized circuit for the Boolean function.
There is a specific labeling for a Karnaugh map for each number
of circuit input variables. A Karnaugh map consists of squares where
each square represents a minterm. Notice that only one variable can
change in any adjacent horizontal or vertical square. Remember that
a minterm is the input pattern where there is a '1' in the output
of a truth table.
After the map is drawn and labeled, a '1' is placed in each square
corresponding to a minterm of the function. Later an 'X' will be
allowed for "don't care" minterms. By convention, no zeros are
written into the map.
Having a filled in map, visual skills and intuition are used to
find the minimum number of rectangles that enclose all the ones.
The rectangles must have sides that are powers of two. No
rectangle is allowed to contain a blank square. The map is a toroid
such that the top row is logically adjacent to the bottom row and
the right column is logically adjacent to the left column. Thus
rectangles do not have to be within the two dimensional map.
The resulting minimized boolean function is written as a sum of
products. Each rectangle represents a product, "and" gate, and
the products are summed, "or gate", to produce the result. A rectangle
that contains both a variable and its complement does not have
that variable in the product term, omit the variable as an input
to the "and" gate.
Basic labeling Minterm numbers Minterms
B=0 B=1 B=0 B=1 B=0 B=1
+---+---+ +---+---+ +---+---+
A=0 | | | A=0 |m0 |m1 | A=0 |__ |_ |
+---+---+ +---+---+ |AB |AB |
A=1 | | | A=1 |m2 |m3 | +---+---+
+---+---+ +---+---+ A=1 | _ | |
|AB |AB |
+---+---+
Truth table Karnaugh map Covering with rectangles
A B | F B=0 B=1 B=0 B=1
----+-- +---+---+ +-----+-----+
0 0 | 0 A=0 | | 1 | | |+---+|
0 1 | 1 m1 +---+---+ A=0 | || 1 ||
1 0 | 1 m2 A=1 | 1 | | | |+---+|
1 1 | 0 +---+---+ +-----+-----+
|+---+| |
A=1 || 1 || |
|+---+| |
+-----+-----+
_ _
Minimized function F = AB + AB
Note: For each covering rectangle, there will be exactly one
product term in the final equation for the function.
Find the variable(s) that are both 1 and 0 in the rectangle.
Such variables will not appear in the product term. Take any
minterm from the covering rectangle, replace 1 with the variable,
replace 0 with the complement of the variable. Cross out the
variables that do not appear. The result is exactly one product
term needed by the final equation of the function.
It is possible to have minterms that are don't care. For these
minterms, place an "X" or "-" in the Karnaugh map rather than
a one. The covering follows the obvious extended rule.
Covering rectangles may include any don't care squares.
Covering rectangles do not have to include don't care squares.
No rectangle can enclose only don't care squares.
A tabular algorithm for producing the minimum two level sum of products
is know as the Quine McClusky method.
You may download and build the software that performs this minimization.
qm.tgz or link to a Linux executable
ln -s /afs/umbc.edu/users/s/q/squire/pub/linux/qm qm
The man page, qm.1 , is in the same directory.
The algorithm may be performed manually using the following steps:
1) Have available the minterms of the function to be minimized.
There may be X's for don't care cases.
2) Create groups of minterms, starting with the minterms with the
fewest number of ones.
All minterms in a group must have the same number of ones and
if any X's, the X's must be in the same position. There may be
some groups with only one minterm.
3) Create new minterms by combining minterms from groups that
differ by a count of one. Two minterms are combined if they
differ in exactly one position. Place an X in that position
of the newly created minterm. Mark the minterms that are
used in combining (they will be deleted at the end of this step).
Basically, take the first minterm from the first group. Compare
this minterm to all minterms in the next group(s) that have
one additional one. Repeat working until the last group is reached.
4) Delete the marked minterms.
5) Repeat steps 2) 3) and 4) until no more minterms are combined.
6) The minimized function is the remaining minterms, deleting any
X's.
Example:
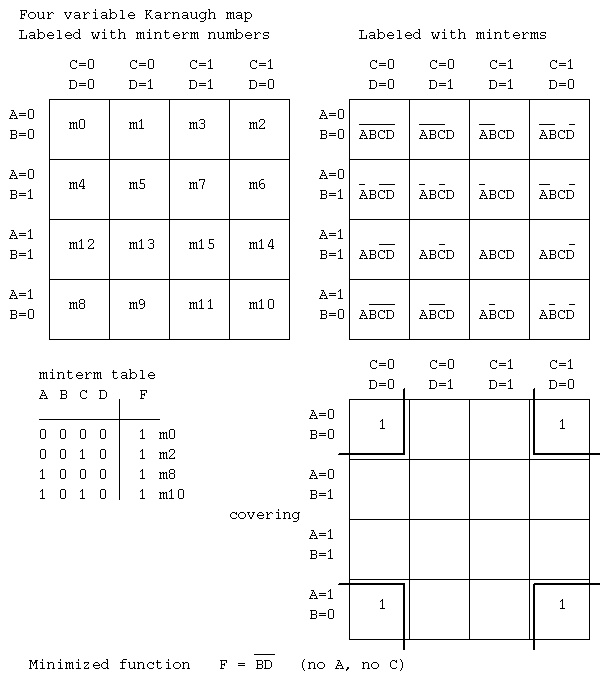
1) Given the minterms
A B C D | F
--------+--
0 0 0 0 | 1 m0
0 0 1 0 | 1 m2
1 0 0 0 | 1 m8
1 0 1 0 | 1 m10
2) Create groups
m0 0 0 0 0 count of 1's is 0
-------
m2 0 0 1 0 count of 1's is 1
m8 1 0 0 0
-------
m10 1 0 1 0 count of 1's is 2
3) Create new minterms by combining
Compare all in first group to all in second group
m0 to m2 0 0 0 0
0 0 1 0
======= they differ in one position
0 0 X 0 combine and put an X in that position
m0 to m8 0 0 0 0
1 0 0 0
======= they differ in one position
X 0 0 0 combine and put an X in that position
Compare all in second group to all in third group
m2 to m10 0 0 1 0
1 0 1 0
======= they differ in one position
X 0 1 0 combine and put an X in that position
m8 to m10 1 0 0 0
1 0 1 0
======= they differ in one position
1 0 X 0 combine and put an X in that position
no more candidates to compare.
4) Delete marked minterms (those used in any combining)
(do not keep duplicates) Thus the minterms are now:
0 0 X 0
X 0 0 0
X 0 1 0
1 0 X 0
2) Repeat grouping (technically there are four groups, although
the number of ones is either zero or one).
0 0 X 0
-------
X 0 0 0
-------
X 0 1 0
-------
1 0 X 0
3) Create new minterms by combining
0 0 X 0
1 0 X 0 any X's must be the same in both
======= they differ in one position
X 0 X 0 combine and put an X in that position
X 0 0 0
X 0 1 0
======= they differ in one position
X 0 X 0 combine and put an X in that position
4) Delete marked minterms (those used in any combining)
(do not keep duplicates) Thus the minterms are now:
X 0 X 0
5) No more combining is possible.
6) The minimized function is the remaining minterms, deleting any
X's. All remaining minterms are prime implicants
A B C D __
X 0 X 0 thus F = BD
In essence, the Quine McClusky algorithm is doing the same
operations as the Karnaugh map. The difference is that no guessing
is used in the Quine McClusky algorithm and "qm" as it is called,
can be (and has been) implemented as a computer program.
A final note on labeling:
It does not matter what names are used for variables.
It does not matter in what order variables are used.
It does not matter if "-" or "X" is used for don't care.
It is important to keep a consistent relation between the bit
positions in minterms and the order of variables.
You may download and build the software that performs this minimization.
qm.tgz or link to a Linux executable
ln -s /afs/umbc.edu/users/s/q/squire/pub/linux/qm qm
The man page, qm.1 , is in the same directory.
More information is at Simulators and parsers
<- previous index next ->