<- previous index next ->
We have arbitrarily scattered boundary points and DOF.
No structure is provided. The problem is to discretize
and build a system of equations, solve the equations,
and determine the values at the DOF.
Simple 1D demonstration
check_nuderiv.c just 6 points
check_nuderiv_c.out check solution
check_nuderiv.java just 6 points
check_nuderiv_java.out check solution
So far, only for 2D and 3D geometry, yet could be generalized.
The basic problem is avoiding singular matrices.
The worse case of arbitrarily scattered points is
when they are uniformly spaced.
The basic non uniform discretization:
nuderiv2d.c use all points
nuderiv2d.h
test_nuderiv2d.c
test_nuderiv2d_c.out
nuderiv2dg.c use good points, less singular
nuderiv2dg.h
test_nuderiv2dg.c
test_nuderiv2dg_c.out
nuderiv2d.java use all points
test_nuderiv2d.java
test_nuderiv2d_java.out
nuderiv2dg.java use good points, less singular
test_nuderiv2dg.java
test_nuderiv2dg_java.out
Now a corner geometry
test_nuderiv2dgc.c
test_nuderiv2dgc_c.out
The basic 3D non uniform discretization:
nuderiv3d.c use all points
nuderiv3d.h
test_nuderiv3d.c
test_nuderiv3d_c.out
nuderiv3dg.c use good points, less singular
nuderiv3dg.h
test_nuderiv3dg.c
test_nuderiv3dg_c.out
nuderiv3dg.java use good points, less singular
test_nuderiv3dg.java
test_nuderiv3dg_java.out
Applying non uniform discretization to a PDE

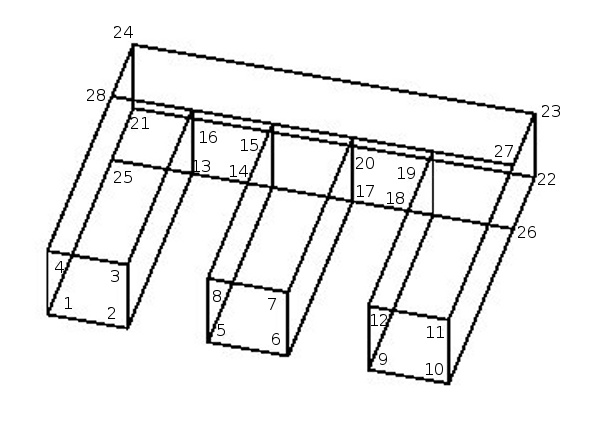 blivet.inp zero based, regular
blivet_nr.inp non regular
pde_blivet.c
pde_blivet_c.out
pde_blivet_nr_c.out
pde_blivet.java
pde_blivet_java.out
pde_blivet_nr_java.out
blivet.inp zero based, regular
blivet_nr.inp non regular
pde_blivet.c
pde_blivet_c.out
pde_blivet_nr_c.out
pde_blivet.java
pde_blivet_java.out
pde_blivet_nr_java.out
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation

 blivet.inp zero based, regular
blivet_nr.inp non regular
pde_blivet.c
pde_blivet_c.out
pde_blivet_nr_c.out
pde_blivet.java
pde_blivet_java.out
pde_blivet_nr_java.out
blivet.inp zero based, regular
blivet_nr.inp non regular
pde_blivet.c
pde_blivet_c.out
pde_blivet_nr_c.out
pde_blivet.java
pde_blivet_java.out
pde_blivet_nr_java.out