CMSC 455 Lecture 36 Some special PDE's

    <- previous    index    next ->

Lecture 36, Some special PDE's


From "A Collection of 2D Elliptic Problems for Testing
      Adaptive Algorithms" by William F. Mitchell

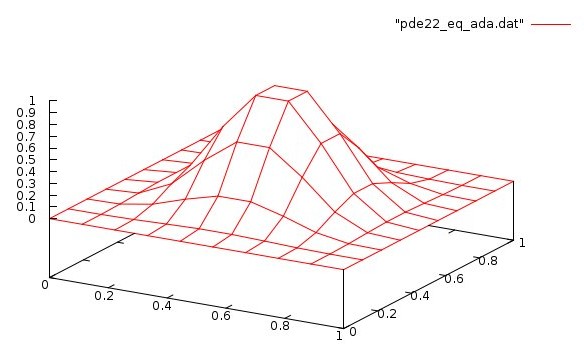
1. Solutions of the form
U(x,y)=2^4p x^p (x-1)^p y^p (y-1)^p  for p=4
PDE Uxx(x,y) + Uyy(x,y) = f(x,y)
boundary unit square



pde22_eq.adb
pde22_eq_ada.out
pde22_eq_ada.dat
pde22_eq_ada.plot
pde22_eq_ada.sh

pde22_eq.c
pde22_eq_c.out
pde22_eq_c.dat
pde22_eq_c.plot
pde22_eq_c.sh

pde22_eq.java
pde22_eq_java.out
pde22_eq_java.dat
pde22_eq_java.plot
pde22_eq_java.sh

pde22_eq.f90
pde22_eq_f90.out
pde22_eq_f90.dat
pde22_eq_f90.plot
pde22_eq_f90.sh

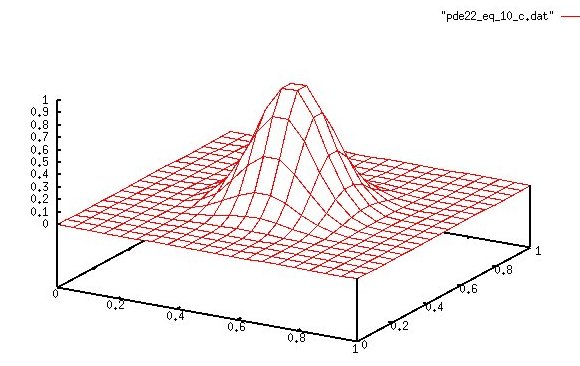
Then U(x,y)=2^4p x^p (x-1)^p y^p (y-1)^p for  p=10



pde22_eq_10.c
pde22_eq_10_c.out
pde22_eq_10_c.dat
pde22_eq_10_c.plot
pde22_eq_10_c.sh

Then U(x,y)=4*(x-1)*(x-3)*(x-3)*(y-1)*(y-3)*(y-3)  p=9



pde22b_eq.java source code
simeq.java source code
rderiv.java source code
pde22b_eq_java.out
pde22b_eq_java.dat
pde22b_eq_java.plot
pde22b_eq_java.sh

Then U(x,y)=5*(x*x+x)*(y*y+y)  p=9



pde22d_eq.java
pde22d_eq_java.out
pde22d_eq_java.dat
pde22d_eq_java.plot
pde22d_eq_java.sh


2. Solutions of the form
alpha = Pi/omega
r = sqrt(x^2+y^2)
theta = atan2(y,x) 0..2Pi
U(x,y)=r^alpha * sin(alpha*theta)
PDE Uxx(x,y) + Uyy(x,y) = 0
boundary x -1..1, y -1..1


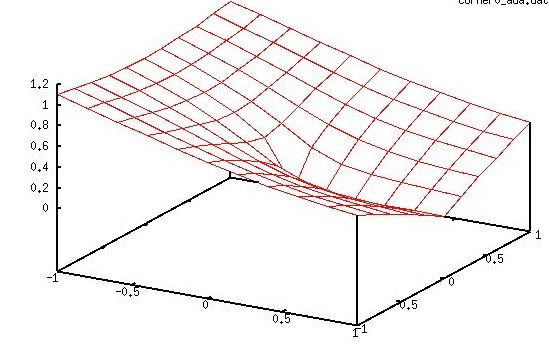Exact solution


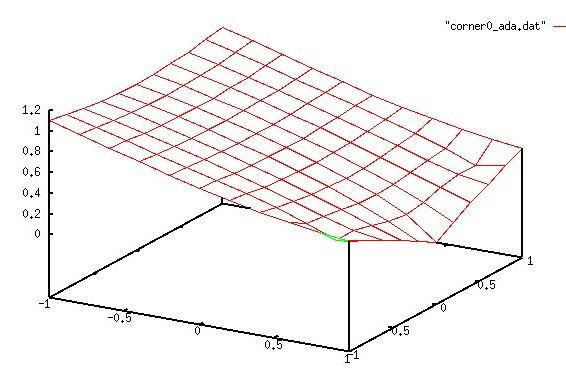nx=11, ny=11 uniformly spaced, computed solution


corner0.adb
corner0_ada.out
corner0_ada.dat
corner0_ada.plot
corner0_ada.sh

corner0.c
corner0_c.out
corner0_c.dat
corner0_c.plot
corner0_c.sh

corner0.java
corner0_java.out
corner0_java.dat
corner0_java.plot
corner0_java.sh

corner0.f90
corner0_f90.out
corner0_f90.dat
corner0_f90.plot
corner0_f90.sh


Makefile and other files for programs listed above
Makefile_spde
nuderiv.adb
inverse.adb
simeq.adb
real_arrays.ads
real_arrays.adb

nuderiv.c
inverse.c
simeq.c
mpf_nuderivd.c
mpf_inverse.c

nuderiv.java
inverse.java
simeq.java

nuderiv.f90
inverse.f90
simeq.f90

Have gnuplot installed to get plots.
Have gnat installed for .adb
Have gcc  installed for .c
Have Java installed for .java
Have gfortran installed for .f90


PDE for Turbulence and Diffusion

pde_turbulence.pdf

diffusion_equation

Generic_scalar_transport_equation

Unusual geometries and using all differentials



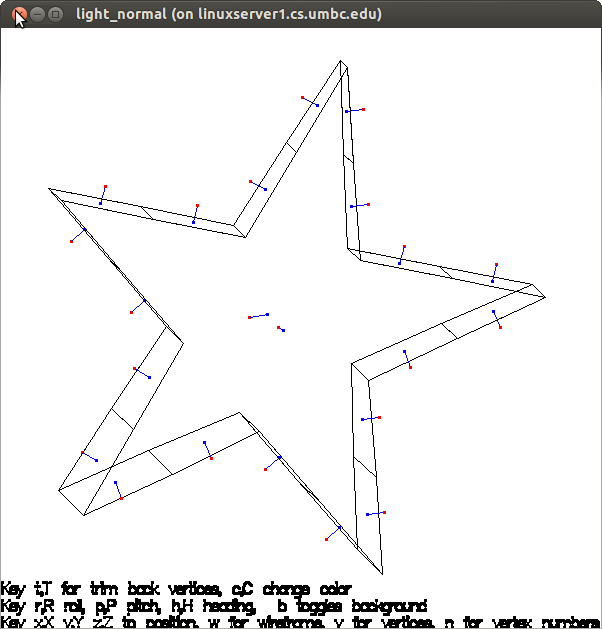The red dot is the positive direction of the normal to the surface.

Plotted with light_normal.c to be sure all surfaces have normal
pointing out. This is needed to be able to determine if a
point is inside the volume and process Neumann boundary conditions.

poly43.txt
All 4th order derivatives in 3 dimensions.

pde_star3t.java
Used in pde_star3t.java.