<- previous index next ->
First look at a computer architecure
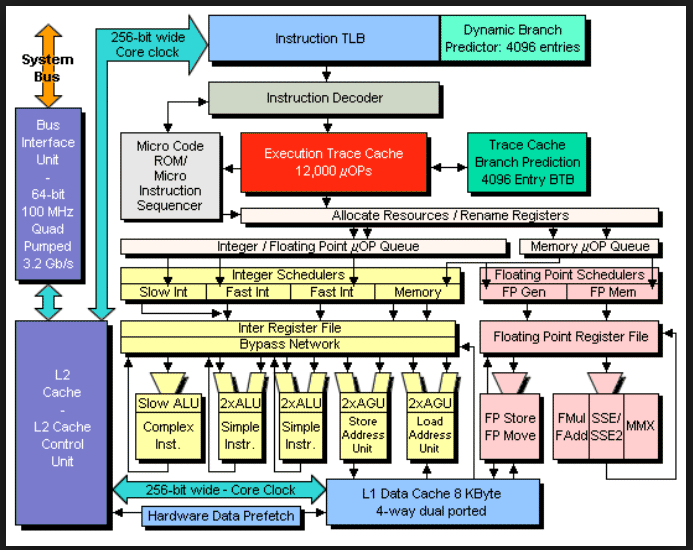Intel block diagram
You should be familiar with programming.
You edit your source code and have it on the disc.
A compiler reads your source code and typically converts
high level language to assembly language as another file on the disc.
The assembler reads the assembly language and produces a
binary object file with machine instructions.
The loader reads object files and creates an executable image.
This course is to provide a basic understanding of how computers
operate internally, e.g. computer architecture and assembly language.
Technically: The computer does not run a "program", the computer
has an operating system that runs a "process". A process starts
with loading the executable image of a program in memory.
A process sets up "segments" of memory with:
A ".text" segment with computer instructions
A ".data" segment with initialized data
A ".rodata" segment with initialized data, read only
A ".bss" segment for variables and arrays
A "stack" for pushing and popping values
A "heap" for dynamically getting more memory
And then the process is executed by having the program
address register set to the first executable instruction
in the process. You will be directly using segments in
your assembly language programs.
Computers store bits, binary digits, in memory and we usually
read the bits, four at a time as hexadecimal. The basic unit
of storage in the computer is two hex digits, eight bits, a byte.
The data may be integers, floating point or characters.
We start this course with a thorough understanding of numbers.
Numbers are represented as the coefficients of powers of a base.
(in plain text, we use "^" to mean, raise to power or exponentiation)
With no extra base indication, expect decimal numbers:
12.34 is a representation of
1*10^1 + 2*10^0 + 3*10^-1 + 4*10^-2 or
10
2
.3
+ .04
------
12.34
Binary numbers, in NASM assembly language, have a trailing B or b.
101.11B is a representation of
1*2^2 + 0*2^1 + 1*2^0 + 1*2^-1 + 1*2^-2 or
4
0
1
.5 (you may compute 2^-n or look up in table below)
+ .25
------
5.75
Converting a decimal number to binary may be accomplished:
Convert 12.34 from decimal to binary
Integer part Fraction part
quotient remainder integer fraction
12/2 = 6 0 .34*2 = 0.68
6/2 = 3 0 .68*2 = 1.36
3/2 = 1 1 .36*2 = 0.72
1/2 = 0 1 .72*2 = 1.44
done .44*2 = 0.88
read up 1100 .88*2 = 1.76
.76*2 = 1.52
.52*2 = 1.04
quit
read down .01010111
answer is 1100.01010111
Powers of 2
Decimal
n -n
2 n 2
1 0 1.0
2 1 0.5
4 2 0.25
8 3 0.125
16 4 0.0625
32 5 0.03125
64 6 0.015625
128 7 0.0078125
256 8 0.00390625
512 9 0.001953125
1024 10 0.0009765625
2048 11 0.00048828125
4096 12 0.000244140625
8192 13 0.0001220703125
16384 14 0.00006103515625
32768 15 0.000030517578125
65536 16 0.0000152587890625
For binary to decimal:
2^3 2^2 2^1 2^0 2^-1 2^-2 2^-3
1 1 1 1 . 1 1 1
8 + 4 + 2 + 1 + .5 + .25 + .125 = 15.875
Binary
n -n
2 n 2
1 0 1.0
10 1 0.1
100 2 0.01
1000 3 0.001
10000 4 0.0001
100000 5 0.00001
1000000 6 0.000001
10000000 7 0.0000001
100000000 8 0.00000001
1000000000 9 0.000000001
10000000000 10 0.0000000001
100000000000 11 0.00000000001
1000000000000 12 0.000000000001
10000000000000 13 0.0000000000001
100000000000000 14 0.00000000000001
1000000000000000 15 0.000000000000001
10000000000000000 16 0.0000000000000001
Hexadecimal
n -n
2 n 2
1 0 1.0
2 1 0.8
4 2 0.4
8 3 0.2
10 4 0.1
20 5 0.08
40 6 0.04
80 7 0.02
100 8 0.01
200 9 0.008
400 10 0.004
800 11 0.002
1000 12 0.001
2000 13 0.0008
4000 14 0.0004
8000 15 0.0002
10000 16 0.0001
Decimal to Hexadecimal to Binary, 4 bits per hex digit
0 0 0000
1 1 0001
2 2 0010
3 3 0011
4 4 0100
5 5 0101
6 6 0110
7 7 0111
8 8 1000
9 9 1001
10 A 1010
11 B 1011
12 C 1100
13 D 1101
14 E 1110
15 F 1111
n n
n 2 hexadecimal 2 decimal approx notation
10 400 1,024 10^3 K kilo
20 100000 1,048,576 10^6 M mega
30 40000000 1,073,741,824 10^9 G giga
40 10000000000 1,099,511,627,776 10^12 T tera
The three representations of negative numbers that have been
used in computers are twos complement, ones complement and
sign magnitude. In order to represent negative numbers, it must
be known where the "sign" bit is placed. All modern binary
computers use the leftmost bit of the computer word as a sign bit.
The examples below use a 4-bit register to show all possible
values for the three representations.
decimal twos complement ones complement sign magnitude
0 0000 0000 0000
1 0001 0001 0001
2 0010 0010 0010
3 0011 0011 0011
4 0100 0100 0100
5 0101 0101 0101
6 0110 0110 0110
7 0111 0111 0111
-7 1001 1000 1111
-6 1010 1001 1110
-5 1011 1010 1101
-4 1100 1011 1100
-3 1101 1100 1011
-2 1110 1101 1010
-1 1111 1110 1001
-8 1000 -0 1111 -0 1000
^ / ^|||
\_ add 1 _/ sign__/ --- magnitude
To get the sign magnitude, convert the decimal to binary and
place a zero in the sign bit for positive, place a one in the
sign bit for negative.
To get the ones complement, convert the decimal to binary,
including leading zeros, then invert every bit. 1->0, 0->1.
To get the twos complement, get the ones complement and add 1.
(Throw away any bits that are outside of the register)
It may seem silly to have a negative zero, but it is
mathematically incorrect to have -(-8) = -8
IEEE Floating point formats
Almost all Numerical Computation arithmetic is performed using
IEEE 754-1985 Standard for Binary Floating-Point Arithmetic.
The two formats that we deal with in practice are the 32 bit and
64 bit formats.
IEEE Floating-Point numbers are stored as follows:
The single format 32 bit has
1 bit for sign, 8 bits for exponent, 23 bits for fraction
The double format 64 bit has
1 bit for sign, 11 bits for exponent, 52 bits for fraction
There is actually a '1' in the 24th and 53rd bit to the left
of the fraction that is not stored. The fraction including
the non stored bit is called a significand.
The exponent is stored as a biased value, not a signed value.
The 8-bit has 127 added, the 11-bit has 1023 added.
A few values of the exponent are "stolen" for
special values, +/- infinity, not a number, etc.
Floating point numbers are sign magnitude. Invert the sign bit to negate.
Some example numbers and their bit patterns:
decimal
stored hexadecimal sign exponent fraction significand
bit in binary
The "1" is not stored
| biased
31 30....23 22....................0 exponent
1.0
3F 80 00 00 0 01111111 00000000000000000000000 1.0 * 2^(127-127)
0.5
3F 00 00 00 0 01111110 00000000000000000000000 1.0 * 2^(126-127)
0.75
3F 40 00 00 0 01111110 10000000000000000000000 1.1 * 2^(126-127)
0.9999995
3F 7F FF FF 0 01111110 11111111111111111111111 1.1111* 2^(126-127)
0.1
3D CC CC CD 0 01111011 10011001100110011001101 1.1001* 2^(123-127)
63 62...... 52 51 ..... 0
1.0
3F F0 00 00 00 00 00 00 0 01111111111 000 ... 000 1.0 * 2^(1023-1023)
0.5
3F E0 00 00 00 00 00 00 0 01111111110 000 ... 000 1.0 * 2^(1022-1023)
0.75
3F E8 00 00 00 00 00 00 0 01111111110 100 ... 000 1.1 * 2^(1022-1023)
0.9999999999999995
3F EF FF FF FF FF FF FF 0 01111111110 111 ... 1.11111* 2^(1022-1023)
0.1
3F B9 99 99 99 99 99 9A 0 01111111011 10011..1010 1.10011* 2^(1019-1023)
|
sign exponent fraction |
before storing subtract bias
Note that an integer in the range 0 to 2^23 -1 may be represented exactly.
Any power of two in the range -126 to +127 times such an integer may also
be represented exactly. Numbers such as 0.1, 0.3, 1.0/5.0, 1.0/9.0 are
represented approximately. 0.75 is 3/4 which is exact.
Some languages are careful to represent approximated numbers
accurate to plus or minus the least significant bit.
Other languages may be less accurate.
The operations of add, subtract, multiply and divide are defined as:
Given x1 = 2^e1 * f1
x2 = 2^e2 * f2 and e2 <= e1
x1 + x2 = 2^e1 *(f1 + 2^-(e1-e2) * f2) f2 is shifted then added to f1
x1 - x2 = 2^e1 *(f1 - 2^-(e1-e2) * f2) f2 is shifted then subtracted from f1
x1 * x2 = 2^(e1+e2) * f1 * f2
x1 / x2 = 2^(e1-e2) * (f1 / f2)
an additional operation is usually needed, normalization.
if the resulting "fraction" has digits to the left of the binary
point, then the fraction is shifted right and one is added to
the exponent for each bit shifted until the result is a fraction.
IEEE 754 Floating Point Standard
Strings of characters
We will use one of many character representations for
character strings, ASCII, one byte per character in a string.
symbol or name symbol or key stroke
key stroke
hexadecimal hexadecimal
decimal decimal
NUL ^@ 00 0 Spc 20 32 @ 40 64 ` 60 96
SOH ^A 01 1 ! 21 33 A 41 65 a 61 97
STX ^B 02 2 " 22 34 B 42 66 b 62 98
ETX ^C 03 3 # 23 35 C 43 67 c 63 99
EOT ^D 04 4 $ 24 36 D 44 68 d 64 100
ENQ ^E 05 5 % 25 37 E 45 69 e 65 101
ACK ^F 06 6 & 26 38 F 46 70 f 66 102
BEL ^G 07 7 ' 27 39 G 47 71 g 67 103
BS ^H 08 8 ( 28 40 H 48 72 h 68 104
TAB ^I 09 9 ) 29 41 I 49 73 i 69 105
LF ^J 0A 10 * 2A 42 J 4A 74 j 6A 106
VT ^K 0B 11 + 2B 43 K 4B 75 k 6B 107
FF ^L 0C 12 , 2C 44 L 4C 76 l 6C 108
CR ^M 0D 13 - 2D 45 M 4D 77 m 6D 109
SO ^N 0E 14 . 2E 46 N 4E 78 n 6E 110
SI ^O 0F 15 / 2F 47 O 4F 79 o 6F 111
DLE ^P 10 16 0 30 48 P 50 80 p 70 112
DC1 ^Q 11 17 1 31 49 Q 51 81 q 71 113
DC2 ^R 12 18 2 32 50 R 52 82 r 72 114
DC3 ^S 13 19 3 33 51 S 53 83 s 73 115
DC4 ^T 14 20 4 34 52 T 54 84 t 74 116
NAK ^U 15 21 5 35 53 U 55 85 u 75 117
SYN ^V 16 22 6 36 54 V 56 86 v 76 118
ETB ^W 17 23 7 37 55 W 57 87 w 77 119
CAN ^X 18 24 8 38 56 X 58 88 x 78 120
EM ^Y 19 25 9 39 57 Y 59 89 y 79 121
SUB ^Z 1A 26 : 3A 58 Z 5A 90 z 7A 122
ESC ^[ 1B 27 ; 3B 59 [ 5B 91 { 7B 123
LeftSh 1C 28 < 3C 60 \ 5C 92 | 7C 124
RighSh 1D 29 = 3D 61 ] 5D 93 } 7D 125
upAro 1E 30 > 3E 62 ^ 5E 94 ~ 7E 126
dnAro 1F 31 ? 3F 63 _ 5F 95 DEL 7F 127
Optional future installation on your personal computer
Throughout this course, we will be writing some assembly language.
This will be for an Intel or Intel compatible computer, e.g. AMD.
The assembler program is "nasm" and can be run on
linux.gl.umbc.edu or on your computer.
If you are running linux on your computer, the command
sudo apt-get install nasm
will install nasm on your computer.
Throughout this course we will work with digital logic and
cover basic VHDL and verilog languages for describing
digital logic. There are free simulators, that will
simulate the operation of your digital logic for both languages
and graphical input simulator logisim.
The commands for installing these on linux are:
sudo apt-get install freehdl
or use Makefile_vhdl from my download directory on linux.gl.umbc.edu
sudo apt-get install iverilog
or use Makefile_verilog from my download directory on linux.gl.umbc.edu
from www.cburch.com/logisim/index.html get logisim
or use Makefile_logisim from my download directory on linux.gl.umbc.edu
These or similar programs may be available for installing
on some versions of Microsoft Windows or Mac OSX.
We will use 64-bit in this course, to expand your options.
In "C" int remains a 32-bit number although we have 64-bit computers
and 64-bit operating systems and 64-bit computers that are still
programmed as 32-bit computers.
test_factorial.c uses int, outputs:
test_factorial.c using int, note overflow
0!=1
1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800
11!=39916800
12!=479001600
13!=1932053504
14!=1278945280
15!=2004310016
16!=2004189184
17!=-288522240
18!=-898433024
test_factorial_long.c uses long int, outputs:
test_factorial_long.c using long int, note overflow
0!=1
1!=1
2!=2
3!=6
4!=24
5!=120
6!=720
7!=5040
8!=40320
9!=362880
10!=3628800
11!=39916800
12!=479001600
13!=6227020800
14!=87178291200
15!=1307674368000
16!=20922789888000
17!=355687428096000
18!=6402373705728000
19!=121645100408832000
20!=2432902008176640000
21!=-4249290049419214848
22!=-1250660718674968576
Well, 13! wrong vs 21! wrong may not be a big deal.
factorial.py by default, outputs:
factorial(0)= 1
factorial(1)= 1
factorial(2)= 2
factorial(3)= 6
factorial(4)= 24
factorial(52)= 80658175170943878571660636856403766975289505440883277824000000000000
Yet, 32-bit signed numbers can only index 2GB of ram, 64-bit are
needed for computers with 4GB, 8GB, 16GB, 32GB etc of ram, available today.
95% of all supercomputers, called HPC, are 64-bit running Linux.
First homework assigned
on web, www.cs.umbc.edu/~squire/cmpe310_hw.shtml
Due in one week. Best to do right after lecture.
<- previous index next ->