<- previous index next ->
Numerical Integration is usually called Numerical Quadrature.
Watch for "int" in this page it is short for "integrate".
Numerical integration could be simple summation, but
in order to get reasonable step size and good accuracy
we need better techniques.
integral f(x) dx from x=a to x=b with step size h=(b-a)/n
using simple summation would be computed:
area = (b-a)/n * ( sum i=0..n-1 f(a+i*h) ) not using f(b)
or
area = (b-a)/(n+1) * ( sum i=0..n f(a+i*h) )
"h" has become the approximation to "dx" using "n" steps.
A larger value of "n" gives a smaller value of "h" and
up to where round off error grows, a better approximation.
Shown is n=9 indicated by red dots.
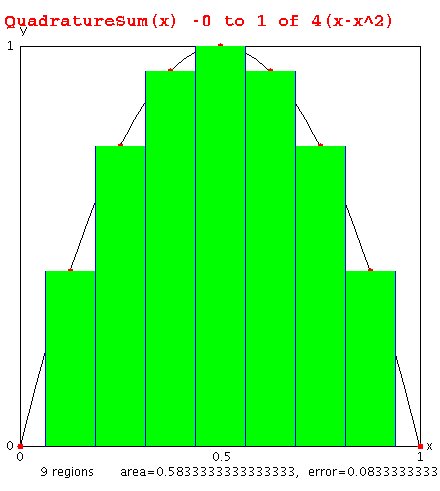 from QuadratureSum.java
Exact solution integral from 0 to 1 of 4(x-x^2) = 2/3 = 0.6666666
from QuadratureSum.java
Exact solution integral from 0 to 1 of 4(x-x^2) = 2/3 = 0.6666666
Trapezoidal method
The Trapezoidal rule approximates the area between x and x+h
as h * (f(x)+f(x+h))/2 , base times average height.
Summing the areas we note that f(a) and f(b) are used once
while the other intermediate f(x) are used twice, thus:
area = (b-a)/n * ( (f(a)+f(b))/2 + sum i=1..n-1 f(a+i*h) )
note: i=0 is f(a) i=n is f(b) thus sum index range 1..n-1
h = (b-a)/n
cutting h in half generally cuts the error in half for large n
Shown is n=8 regions based on 7 sums plus (f(a)+f(b))/2
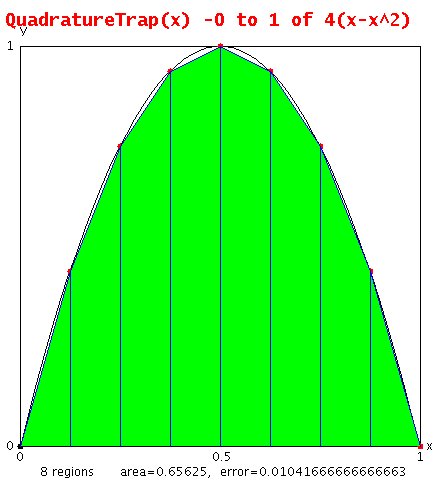 from QuadratureTrap.java
trapezoide.py Trapezoidal Integration
output is:
trapezoide.py running
trap_int area under x*x from 1.0 to 2.0 = 2.335
trapezoide.py finished
or trapezoide.py3 Trapezoidal Integration
trapezoide.java Trapezoidal Integration
output is:
trapezoide.java running
trap_int area under x*x from 1.0 to 2.0 = 2.3350000000000004
trapezoide.java finished
You do not need to use equal step sizes.
For better accuracy with trapazoidal integration,
use smaller step size where slope is largest.
Generally this requires more steps.
from QuadratureTrap.java
trapezoide.py Trapezoidal Integration
output is:
trapezoide.py running
trap_int area under x*x from 1.0 to 2.0 = 2.335
trapezoide.py finished
or trapezoide.py3 Trapezoidal Integration
trapezoide.java Trapezoidal Integration
output is:
trapezoide.java running
trap_int area under x*x from 1.0 to 2.0 = 2.3350000000000004
trapezoide.java finished
You do not need to use equal step sizes.
For better accuracy with trapazoidal integration,
use smaller step size where slope is largest.
Generally this requires more steps.
Better accuracy
In order to get better accuracy with fewer evaluations of
the function, f(x), we have found a way to choose the values
of x and to apply a weight, w(x) to each evaluation of f(x).
The integral is evaluated using:
area = sum i=1..n w(i)*f(x(i))
The w(i) and x(i) are computed using the Legendre polynomials
covered in the previous lecture. The numerical analysis shows
that using n evaluations we obtain accuracy about equal to
fitting the f(x(i)) with an nth order polynomial and accurately
computing the integral using that nth order polynomial.
Some values of weights w(i) and ordinates x(i) -1 < x < 1 are:
x[1]= 0.0000000000000E+00, w[1]= 2.0000000000000E+00
x[1]= -5.7735026918963E-01, w[1]= 1.0000000000000E-00
x[2]= 5.7735026918963E-01, w[2]= 1.0000000000000E-00
x[1]= -7.7459666924148E-01, w[1]= 5.5555555555555E-01
x[2]= 0.0000000000000E+00, w[2]= 8.8888888888889E-01
x[3]= 7.7459666924148E-01, w[3]= 5.5555555555555E-01
x[1]= -8.6113631159405E-01, w[1]= 3.4785484513745E-01
x[2]= -3.3998104358486E-01, w[2]= 6.5214515486255E-01
x[3]= 3.3998104358486E-01, w[3]= 6.5214515486255E-01
x[4]= 8.6113631159405E-01, w[4]= 3.4785484513745E-01
x[1]= -9.0617984593866E-01, w[1]= 2.3692688505618E-01
x[2]= -5.3846931010568E-01, w[2]= 4.7862867049937E-01
x[3]= 0.0000000000000E+00, w[3]= 5.6888888888889E-01
x[4]= 5.3846931010568E-01, w[4]= 4.7862867049937E-01
x[5]= 9.0617984593866E-01, w[5]= 2.3692688505618E-01
x[1]= -9.3246951420315E-01, w[1]= 1.7132449237916E-01
x[2]= -6.6120938646626E-01, w[2]= 3.6076157304814E-01
x[3]= -2.3861918608320E-01, w[3]= 4.6791393457269E-01
x[4]= 2.3861918608320E-01, w[4]= 4.6791393457269E-01
x[5]= 6.6120938646626E-01, w[5]= 3.6076157304814E-01
x[6]= 9.3246951420315E-01, w[6]= 1.7132449237916E-01
For a range from a to b, new_x[i] = a+(x[i]+1)*(b-a)/2
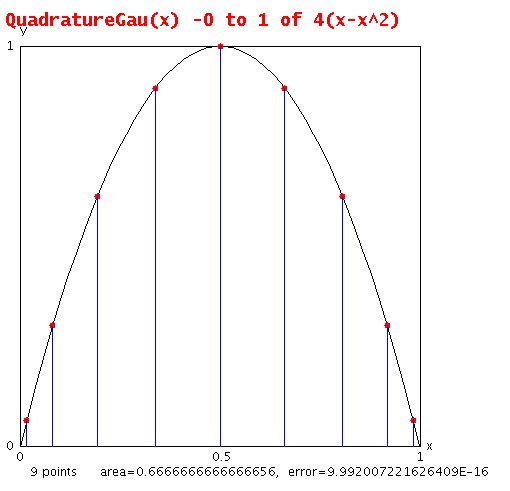 from QuadratureGau.java
and gauleg.java
Using the function gaulegf a typical integration could be:
double x[9], w[9] for 8 points
a = 0.5; integrate sin(x) from a to b
b = 1.0;
n = 8;
gaulegf(a, b, x, w, n); x's adjusted for a and b
area = 0.0;
for(j=1; j<=n; j++)
area = area + w[j]*sin(x[j]);
The following programs, gauleg for Gauss Legendre integration,
computes the x(i) and w(i) for various values of n. The
integration is tested on a constant f(x)=1.0 and then on
integral sin(x) from x=0.5 to x=1.0
integral exp(x) from x=0.5 to x=5.0
integral ((x^x)^x)*(x*(log(x)+1)+x*log(x)) from x=0.5 to x=5.0
This is labeled "mess" in output files.
Note how the accuracy increases with increasing values of n,
then, no further accuracy is accomplished with larger n.
Also note, the n where best numerical accuracy is achieved
is a far smaller n than where round off error would be
significant.
from QuadratureGau.java
and gauleg.java
Using the function gaulegf a typical integration could be:
double x[9], w[9] for 8 points
a = 0.5; integrate sin(x) from a to b
b = 1.0;
n = 8;
gaulegf(a, b, x, w, n); x's adjusted for a and b
area = 0.0;
for(j=1; j<=n; j++)
area = area + w[j]*sin(x[j]);
The following programs, gauleg for Gauss Legendre integration,
computes the x(i) and w(i) for various values of n. The
integration is tested on a constant f(x)=1.0 and then on
integral sin(x) from x=0.5 to x=1.0
integral exp(x) from x=0.5 to x=5.0
integral ((x^x)^x)*(x*(log(x)+1)+x*log(x)) from x=0.5 to x=5.0
This is labeled "mess" in output files.
Note how the accuracy increases with increasing values of n,
then, no further accuracy is accomplished with larger n.
Also note, the n where best numerical accuracy is achieved
is a far smaller n than where round off error would be
significant.
Downloadable code in C, Python, Fortran, Java, Ada and Matlab
Choose your favorite language and study the .out file
then look over the source code.
Just testing gaulegf:
integrate3d.java calculus
integrate3d_java.out numerical
gauleg.py function is gaulegf
test_gauleg.py
test_gauleg_py.out
gauleg.py3 function is gaulegf
test_gauleg.py3
test_gauleg_py3.out
gaulegf.java
test_gauleg.java
test_gauleg_java.out
gaulegf.h
gaulegf.c
test_gaulegf.c
test_gaulegf_c.out
test_gaulegf.cpp C++
test_gaulegf_cpp.out result
test_gaulegf.rb Ruby
test_gaulegf_rb.out result
gaulegf.adb
test_gaulegf.adb
test_gaulegf_ada.out
gaulegf.f90 original
Look near end of .out file, note convergence to exact value at end.
integral sin(x) from x=0.5 to x=1.0 for order 2 through 10
integral exp(x) from x=0.5 to x=5.0 for order 2 through 10
integral ((x^x)^x)*(x*(log(x)+1)+x*log(x)) from x=0.5 to x=5.0
This is labeled "mess" in output files. order 2 through 30
gauleg.c
gauleg_c.out
gauleg.f90
gauleg_f90.out
gauleg.for
gauleg_for.out
gauleg.java
gauleg_java.out
gauleg.adb
gauleg_ada.out
gaulegf.m
gauleg.m
gauleg_m.out
On Linux, you may use octave rather than MatLab.
Higher dimension, more independent variables
Multidimensional integration extends easily by using
gaulegf(ax, bx, xx, wx, nx); x's adjusted for ax and bx
gaulegf(ay, by, yy, wy, ny); y's adjusted for ay and by
volume = 0.0;
for(i=1; i<=nx; i++)
for(j=1; j<=ny; j++)
volume = volume + wx[i]*wy[j]*f(xx[i],yy[j]);
gaulegf(ax, bx, xx, wx, nx); x's adjusted for ax and bx
gaulegf(ay, by, yy, wy, ny); y's adjusted for ay and by
gaulegf(az, bz, zz, wz, nz); z's adjusted for az and bz
volume4d = 0.0;
for(i=1; i<=nx; i++)
for(j=1; j<=ny; j++)
for(k=1; k<=nz; k++)
volume4d = volume4d + wx[i]*wy[j]*wz[k]*f(xx[i],yy[j],zz[k]);
Volume code as shown in:
int2d.c
int2d_c.out
Additional reference books include:
"Handbook of Mathematical Functions" by Abramowitz and Stegun
A classic reference book on numerical integration and differentiation.
"Numerical Recipes in Fortran" by Press, Teukolsky, Vetterling and Flannery
There is also a "Numerical recipes in C" yet in my copy, there have
been a number of errors in the C code due to poor translation from Fortran.
Many very good numerical codes for general purpose and special purposes.
Integration of functions over triangles
An impressive example of quadrature over triangles is shown
by using Gauss Legendre integration coordinates rather than
splitting a triangle into smaller congruent triangles.
The routine "tri_split" converts a single triangle into four
congruent triangles that exactly cover the initial triangle.
Linear quadrature then uses just the center point of the
split, four equal area, triangles.
triquad.java triangle quadrature
test_triquad.java test
test_triquad.out results, see last two sets
Reducing the step size improves integration accuracy.
In two or more dimensions, reducing area, volume, etc.
improves integration accuracy. Two sets of triangle
splitting are shown below. Using higher order integration
provides more integration accuracy than smaller step size,
smaller area, volume, etc.
From tri_split.java
and test_tri_split.java
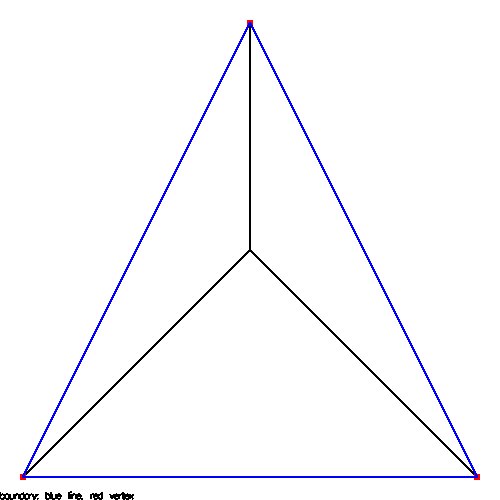
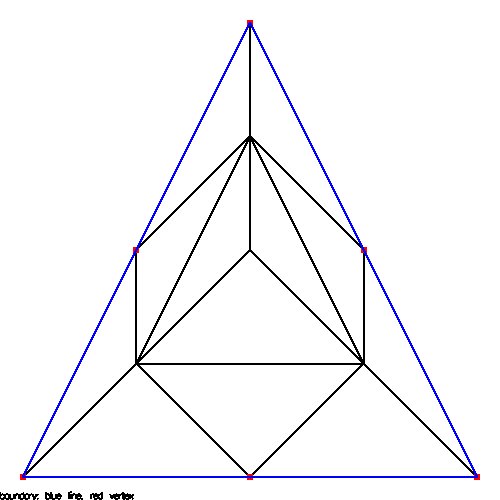
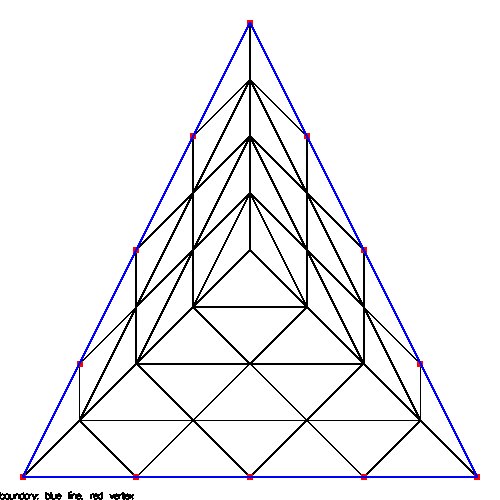
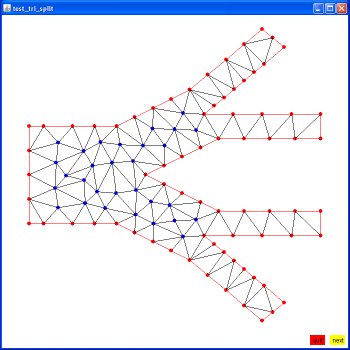
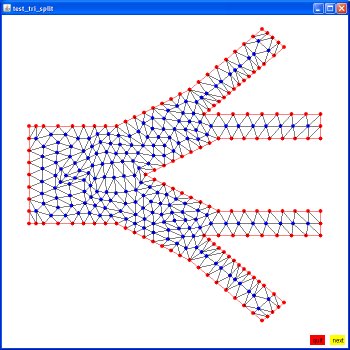
 These will appear later in the solution of
partial differential equations using the Finite Element Method.
These will appear later in the solution of
partial differential equations using the Finite Element Method.
determine if a point is inside a polygon
point_in_poly.c
point_in_poly_c.out
point_in_poly.java
point_in_poly_java.out
Digitizing curves into computer
Scan the curve you want to digitize, sample curves listed below.
Compile Digitize.java
Run java Digitize your.jpg > your.out
Edit your.out to suit your needs. Output is scaled to your first 3 points.
(0,0) (1,0) (0,1)
Additional binary graphics files are:
pi.gif
curve.jpg
c6thrust.jpg
chess2.png
Digitize.out some output from curve.jpg
When working with calculus, you may encounter the "divergence theorem"
For a vector function F in a volume V with surface S
integrate over volume (∇˙F)dV =
integrate over surface (F˙normal)dS
 Just for fun, I programmed a numerical test to check the theorem
for one specific case: program and results of run
divergence_theorem.c
divergence_theorem_c.out
Just for fun, I programmed a numerical test to check the theorem
for one specific case: program and results of run
divergence_theorem.c
divergence_theorem_c.out
The general form of the trapezoidal integration.
a = integral y(x) dx over a set of increasing values of x, x_1 to x_n,
a = sum i=1 to i=n-1 of (x_i+1 - x_i) * (y(x_i) + y(x_i+1))/2
The (x_i+1 - x_i) is a variable version of h.
For best accuracy, pick x values where slope is changing,
in general use dx smaller for larger slope.
HW3 is assigned
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation
 from QuadratureSum.java
Exact solution integral from 0 to 1 of 4(x-x^2) = 2/3 = 0.6666666
from QuadratureSum.java
Exact solution integral from 0 to 1 of 4(x-x^2) = 2/3 = 0.6666666
 from QuadratureTrap.java
trapezoide.py Trapezoidal Integration
output is:
trapezoide.py running
trap_int area under x*x from 1.0 to 2.0 = 2.335
trapezoide.py finished
or trapezoide.py3 Trapezoidal Integration
trapezoide.java Trapezoidal Integration
output is:
trapezoide.java running
trap_int area under x*x from 1.0 to 2.0 = 2.3350000000000004
trapezoide.java finished
You do not need to use equal step sizes.
For better accuracy with trapazoidal integration,
use smaller step size where slope is largest.
Generally this requires more steps.
from QuadratureTrap.java
trapezoide.py Trapezoidal Integration
output is:
trapezoide.py running
trap_int area under x*x from 1.0 to 2.0 = 2.335
trapezoide.py finished
or trapezoide.py3 Trapezoidal Integration
trapezoide.java Trapezoidal Integration
output is:
trapezoide.java running
trap_int area under x*x from 1.0 to 2.0 = 2.3350000000000004
trapezoide.java finished
You do not need to use equal step sizes.
For better accuracy with trapazoidal integration,
use smaller step size where slope is largest.
Generally this requires more steps.
 from QuadratureGau.java
and gauleg.java
Using the function gaulegf a typical integration could be:
double x[9], w[9] for 8 points
a = 0.5; integrate sin(x) from a to b
b = 1.0;
n = 8;
gaulegf(a, b, x, w, n); x's adjusted for a and b
area = 0.0;
for(j=1; j<=n; j++)
area = area + w[j]*sin(x[j]);
The following programs, gauleg for Gauss Legendre integration,
computes the x(i) and w(i) for various values of n. The
integration is tested on a constant f(x)=1.0 and then on
integral sin(x) from x=0.5 to x=1.0
integral exp(x) from x=0.5 to x=5.0
integral ((x^x)^x)*(x*(log(x)+1)+x*log(x)) from x=0.5 to x=5.0
This is labeled "mess" in output files.
Note how the accuracy increases with increasing values of n,
then, no further accuracy is accomplished with larger n.
Also note, the n where best numerical accuracy is achieved
is a far smaller n than where round off error would be
significant.
from QuadratureGau.java
and gauleg.java
Using the function gaulegf a typical integration could be:
double x[9], w[9] for 8 points
a = 0.5; integrate sin(x) from a to b
b = 1.0;
n = 8;
gaulegf(a, b, x, w, n); x's adjusted for a and b
area = 0.0;
for(j=1; j<=n; j++)
area = area + w[j]*sin(x[j]);
The following programs, gauleg for Gauss Legendre integration,
computes the x(i) and w(i) for various values of n. The
integration is tested on a constant f(x)=1.0 and then on
integral sin(x) from x=0.5 to x=1.0
integral exp(x) from x=0.5 to x=5.0
integral ((x^x)^x)*(x*(log(x)+1)+x*log(x)) from x=0.5 to x=5.0
This is labeled "mess" in output files.
Note how the accuracy increases with increasing values of n,
then, no further accuracy is accomplished with larger n.
Also note, the n where best numerical accuracy is achieved
is a far smaller n than where round off error would be
significant.





 These will appear later in the solution of
partial differential equations using the Finite Element Method.
These will appear later in the solution of
partial differential equations using the Finite Element Method.
 Just for fun, I programmed a numerical test to check the theorem
for one specific case: program and results of run
divergence_theorem.c
divergence_theorem_c.out
Just for fun, I programmed a numerical test to check the theorem
for one specific case: program and results of run
divergence_theorem.c
divergence_theorem_c.out