<- previous index next ->
Just extending seventh order PDE in four dimensions, to eight dimensions
Desired solution is U(x,y,z,t,u,v,w,p), given PDE:
∇4U + 2 ∇2U + 8 U = f(x,y,z,t,u,v,w,p)
∂4U(x,y,z,t,u,v,w,p)/∂x4 + ∂4U(x,y,z,t,u,v,w,p)/∂y4 +
∂4U(x,y,z,t,u,v,w,p)/∂z4 + ∂4U(x,y,z,t,u,v,w,p)/∂t4 +
∂4U(x,y,z,t,u,v,w,p)/∂u4 + ∂4U(x,y,z,t,u,v,w,p)/∂v4 +
∂4U(x,y,z,t,u,v,w,p)/∂w4 + ∂4U(x,y,z,t,u,v,w,p)/∂p4 +
2 ∂2U(x,y,z,t,u,v,w,p)/∂x2 + 2 ∂2U(x,y,z,t,u,v,w,p)/∂y2 +
2 ∂2U(x,y,z,t,u,v,w,p)/∂z2 + 2 ∂2U(x,y,z,t,u,v,w,p)/∂t2 +
2 ∂2U(x,y,z,t,u,v,w,p)/∂u2 + 2 ∂2U(x,y,z,t,u,v,w,p)/∂v2 +
2 ∂2U(x,y,z,t,u,v,w,p)/∂w2 + 2 ∂2U(x,y,z,t,u,v,w,p)/∂p2 +
8 U(x,y,z,t,u,v,w,p) = f(x,y,z,t,u,v,w,p)
Test a fourth order PDE in eight dimensions.
∇4U + 2 ∇2U + 8 U = f(x,y,z,t,u,v,w,p)
pde48hn_eq.java solver source code
pde48hn_eq_java.out verification output
∇4U + 2 ∇2U + 8 U = f(x,y,z,t,u,v,w,p)
pde48hn_eq.c solver source code
pde48hn_eq_c.out verification output
pde48hn_eq.adb solver source code
pde48hn_eq_ada.out verification output
pde48h_eq.adb solver source code
pde48h_eq_ada.out verification output
Some programs above also need:
nuderiv.java basic non uniform grid derivative
rderiv.java basic uniform grid derivative
simeq.java basic simultaneous equation
deriv.h basic derivatives
deriv.c basic derivatives
real_arrays.ads 2D arrays and operations
real_arrays.adb 2D arrays and operations
integer_arrays.ads 2D arrays and operations
integer_arrays.adb 2D arrays and operations
rderiv.adb derivative computation
inverse.adb inverse computation
Plotted output from pde48hn_eq.java execution
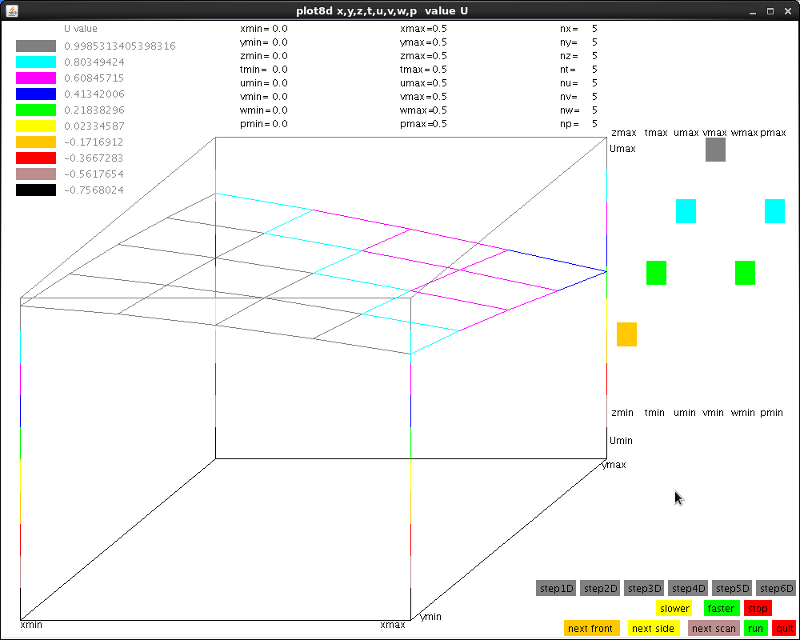 plot8d.java source code
User can select any two variables for 3D view.
User can select values for other variables, option to run all cases.
Then, going to a spherical coordinate system in 8 dimensions
gen_8d_sphere.c source equations
gen_8d_sphere_c.out verification output
plot8d.java source code
User can select any two variables for 3D view.
User can select values for other variables, option to run all cases.
Then, going to a spherical coordinate system in 8 dimensions
gen_8d_sphere.c source equations
gen_8d_sphere_c.out verification output
The above was all Cartesian Coordinates, now Spherical Coordinates
faces.c source code for output
faces.out output for n dimensional cube and spheretest_faces.c source code for test
test_faces.out output of test
faces.java source code for output
faces_java.out output for n dimensional cube and sphere
test_faces.java source code for test
test_faces_java.out equations and test
faces.py source code for output
faces_py.out output for n dimensional cube and sphere
faces.java running, data for various n-cubes, n-spheres, n dimensions
edge length L for cubes, radius R for spheres
0-cube point
vertices = 1
n=1-cube line
edges = 1 length=L
vertices = 2
n=2-cube square
2D faces = 1 area= L^2
edges = 4 length=4*L
vertices = 4
n=3-cube cube
cubes = 1 volume= L^3
2D faces = 6 area= 6*L^2
edges = 12 length=12*L
vertices = 8
n=4-cube
4-cubes = 1 volume= L^4
cubes = 8 volume= 8*L^3
2D faces = 24 area= 24*L^2
edges = 32 length=32*L
vertices = 16
n=5-cube
5-cubes = 1 volume= L^5
4-cubes = 10 volume=10*L^4
cubes = 40 volume=40*L^3
2D faces = 80 area= 80*L^2
edges = 80 length=80*L
vertices = 32
n=6-cube
6-cubes = 1 volume= L^6
5-cubes = 12 volume= 12*L^5
4-cubes = 60 volume= 60*L^4
cubes = 160 volume=160*L^3
2D faces = 240 area= 240*L^2
edges = 192 length=192*L
vertices = 64
n=7-cube
7-cubes = 1 volume= L^7
6-cubes = 14 volume= 14*L^6
5-cubes = 84 volume= 84*L^5
4-cubes = 280 volume=280*L^4
cubes = 560 volume=560*L^3
2D faces = 672 area= 672*L^2
edges = 448 length=448*L
vertices = 128
n=8-cube
8-cubes = 1 volume= L^8
7-cubes = 16 volume= 16*L^7
6-cubes = 112 volume= 112*L^6
5-cubes = 448 volume= 448*L^5
4-cubes = 1120 volume=1120*L^4
cubes = 1792 volume=17928L^3
2D faces = 1792 area= 1792*L^2
edges = 1024 length=1024*L
vertices = 256
n=9-cube
9-cubes = 1 volume= L^9
8-cubes = 18 volume= 18*L^8
7-cubes = 144 volume= 144*L^7
6-cubes = 672 volume= 672*L^6
5-cubes = 2016 volume=2016*L^5
4-cubes = 4032 volume=4032*L^4
cubes = 5376 volume=5376*L^3
2D faces = 4608 area= 4608*L^2
edges = 2304 length=2304*L
vertices = 512
n=10-cube
10-cubes = 1 volume= L^10
9-cubes = 20 volume= 20*L^9
8-cubes = 180 volume= 180*L^8
7-cubes = 960 volume= 960*L^7
6-cubes = 3360 volume= 3360*L^6
5-cubes = 8064 volume= 8064*L^5
4-cubes = 13440 volume=13440*L^4
cubes = 15360 volume=15360*L^3
2D faces = 11520 area= 11520*L^2
edges = 5120 length= 5120*L
vertices = 1024
cubes of n dimensions
with edge length E, n>=3, volume = E^n, area=(2D faces)*E*E
n-cube has 2^n vertex, with n edges at each vertex
n>=m, there are pwr2(n-m)*comb(n,m) n-m sub cubes
Spheres up to 10 dimensions
D-1 surface D volume
2D circle 2 Pi R 1 Pi R^2
3D sphere 4 Pi R^2 4/3 Pi R^3
4D 4-sphere 2 Pi^2 R^3 1/2 Pi^2 R^4
5D 5-sphere 8/3 Pi^2 R^4 8/15 Pi^2 R^5
6D 6-sphere 1 Pi^3 R^5 1/6 Pi^3 R^6
7D 7-sphere 16/15 Pi^3 R^6 16/105 Pi^3 R^7
8D 8-sphere 1/3 Pi^4 R^7 1/24 Pi^4 R^8
9D 9-sphere 32/105 Pi^4 R^8 32/945 Pi^4 R^9
10D 10-sphere 1/12 Pi^5 R^9 1/120 Pi^5 R^10
volume V_n(R)= Pi^(n/2) R^n / gamma(n/2+1)
gamma(integer) = factorial(integer-1) gamma(5) = 24
gamma(1/2) = sqrt(Pi), gamma(n/2+1) = (2n)! sqrt(Pi)/(4^n n!)
or V_2k(R) = Pi^k R^2k/k! , V_2k+1 = 2 k! (4Pi)^k R^(2k+1)/(2k+1)!
surface area A_n(R) = d/dR V_n(R)
one definition of sequence of n-spheres
a1, a2, a3, a4, a5, a6, a7 are angles, typ: theta, phi, ...
x1, x2, x3, x4, x5, x6, x7, x8 are orthogonal coordinates
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 + x6^2 + x7^2 +x8^2 = R^2
Radius R = sqrt(R^2)
2D circle
x1 = R cos(a1) typ: x theta
x2 = R sin(a1) typ: y theta
a1 = arctan(x2/x1) or a1 = acos(x1/R)
3D sphere
x1 = R cos(a1) typ: z phi
x2 = R sin(a1) cos(a2) typ: x phi theta
x3 = R sin(a1) sin(a2) typ: y phi theta
a1 = arctan(sqrt(x2^2+x3^2)/x1) or a1 = acos(x1/R)
a2 = arctan(x3/x2) or a2 = acos(x2/sqrt(x2^2+x3^2))
4D 4-sphere continuing systematic notation, notice pattern
x1 = R cos(a1)
x2 = R sin(a1) cos(a2)
x3 = R sin(a1) sin(a2) cos(a3)
x4 = R sin(a1) sin(a2) sin(a3)
a1 = acos(x1/sqrt(x1^2+x2^2+x3^2+x4^2))
a2 = acos(x2/sqrt(x2^2+x3^2+x4^2))
a3 = acos(x3/sqrt(x3^2+x4^2)) if x4>=0
a3 = 2 Pi - acos(x3/sqrt(x3^2+x4^2)) if x4<0
5D 5-sphere
x1 = R cos(a1)
x2 = R sin(a1) cos(a2)
x3 = R sin(a1) sin(a2) cos(a3)
x4 = R sin(a1) sin(a2) sin(a3) cos(a4)
x5 = R sin(a1) sin(a2) sin(a3) sin(a4)
a1 = acos(x1/sqrt(x1^2+x2^2+x3^2+x4^2+x5^2))
a2 = acos(x2/sqrt(x2^2+x3^2+x4^2+x5^2))
a3 = acos(x3/sqrt(x3^2+x4^2+x5^2))
a4 = acos(x4/sqrt(x4^2+x5^2)) if x5>=0
a4 = 2 Pi - acos(x4/sqrt(x4^2+x5^2)) if x5<0
6D 6-sphere
x1 = R cos(a1)
x2 = R sin(a1) cos(a2)
x3 = R sin(a1) sin(a2) cos(a3)
x4 = R sin(a1) sin(a2) sin(a3) cos(a4)
x5 = R sin(a1) sin(a2) sin(a3) sin(a4) cos(a5)
x6 = R sin(a1) sin(a2) sin(a3) sin(a4) sin(a5)
a1 = acos(x1/sqrt(x1^2+x2^2+x3^2+x4^2+x5^2+x6^2))
a2 = acos(x2/sqrt(x2^2+x3^2+x4^2+x5^2+x6^2))
a3 = acos(x3/sqrt(x3^2+x4^2+x5^2+x6^2))
a4 = acos(x4/sqrt(x4^2+x5^2+x6^2))
a5 = acos(x5/sqrt(x5^2+x6^2)) if x6>=0
a5 = 2 Pi - acos(x5/sqrt(x5^2+x6^2)) if x6<0
7D 7-sphere
x1 = R cos(a1)
x2 = R sin(a1) cos(a2)
x3 = R sin(a1) sin(a2) cos(a3)
x4 = R sin(a1) sin(a2) sin(a3) cos(a4)
x5 = R sin(a1) sin(a2) sin(a3) sin(a4) cos(a5)
x6 = R sin(a1) sin(a2) sin(a3) sin(a4) sin(a5) cos(a6)
x7 = R sin(a1) sin(a2) sin(a3) sin(a4) sin(a5) sin(a6)
a1 = acos(x1/sqrt(x1^2+x2^2+x3^2+x4^2+x5^2+x6^2+x7^2))
a2 = acos(x2/sqrt(x2^2+x3^2+x4^2+x5^2+x6^2+x7^2))
a3 = acos(x3/sqrt(x3^2+x4^2+x5^2+x6^2+x7^2))
a4 = acos(x4/sqrt(x4^2+x5^2+x6^2+x7^2))
a5 = acos(x5/sqrt(x5^2+x6^2+x7^2))
a6 = acos(x6/sqrt(x6^2+x6^2)) if x7>=0
a6 = 2 Pi - acos(x6/sqrt(x6^2+x7^2)) if x7<0
8D 8-sphere
x1 = R cos(a1)
x2 = R sin(a1) cos(a2)
x3 = R sin(a1) sin(a2) cos(a3)
x4 = R sin(a1) sin(a2) sin(a3) cos(a4)
x5 = R sin(a1) sin(a2) sin(a3) sin(a4) cos(a5)
x6 = R sin(a1) sin(a2) sin(a3) sin(a4) sin(a5) cos(a6)
x7 = R sin(a1) sin(a2) sin(a3) sin(a4) sin(a5) sin(a6) cos(a7)
x8 = R sin(a1) sin(a2) sin(a3) sin(a4) sin(a5) sin(a6) sin(a7)
a1 = acos(x1/sqrt(x1^2+x2^2+x3^2+x4^2+x5^2+x6^2+x7^2+x8^2))
a2 = acos(x2/sqrt(x2^2+x3^2+x4^2+x5^2+x6^2+x7^2+x8^2))
a3 = acos(x3/sqrt(x3^2+x4^2+x5^2+x6^2+x7^2+x8^2))
a4 = acos(x4/sqrt(x4^2+x5^2+x6^2+x7^2+x8^2))
a5 = acos(x5/sqrt(x5^2+x6^2+x7^2+x8^2))
a6 = acos(x6/sqrt(x5^2+x6^2+x7^2+x8^2))
a7 = acos(x7/sqrt(x7^2+x8^2)) if x8>=0
a7 = 2 Pi - acos(x7/sqrt(x7^2+x8^2)) if x8<0
faces.java finished
It is left as an exercise to student to develop equations
for gradient and laplacian 4D to 8D spheres.
You won't find many open source or commercial 8D PDE packages
many lesser problems have many open source and commercial packages
en.wikipedia.org/wiki/list_of_finite_element_software_packages
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation
 plot8d.java source code
User can select any two variables for 3D view.
User can select values for other variables, option to run all cases.
Then, going to a spherical coordinate system in 8 dimensions
gen_8d_sphere.c source equations
gen_8d_sphere_c.out verification output
plot8d.java source code
User can select any two variables for 3D view.
User can select values for other variables, option to run all cases.
Then, going to a spherical coordinate system in 8 dimensions
gen_8d_sphere.c source equations
gen_8d_sphere_c.out verification output