<- previous index next ->
Extending PDE's to toroid geometry
solve PDE in toroid boundary
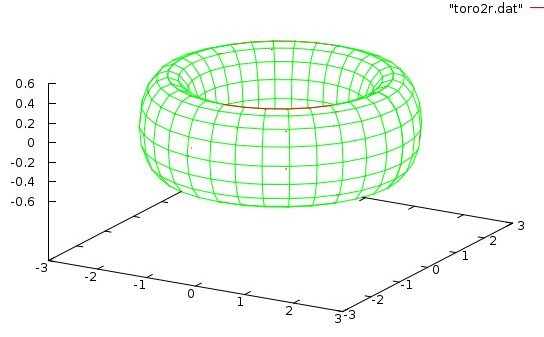
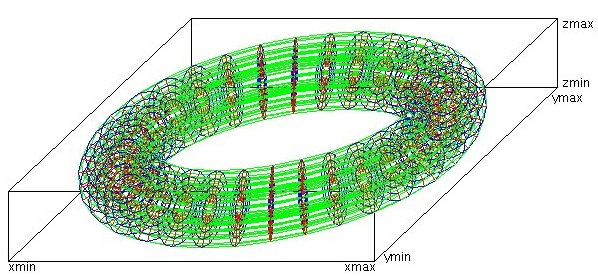 First refinement
First refinement
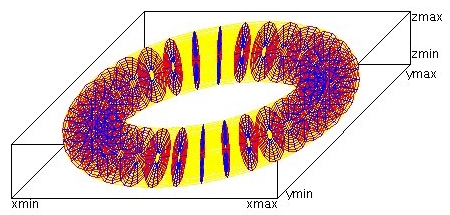 Another view of refinement
Toroid center at 0,0,0 can be translated and rotated
r1, r2, theta, phi mapped to x,y,z
x = (r1+r2*sin(phi))*cos(theta)
y = (r1+r2*sin(phi))*sin(theta)
z = r2 * cos(phi)
0 ≤ theta ≤ 2Pi 0 ≤ phi ≤ 2Pi 0 < r2 < r1
Area = (2*Pi*r1)*(2*Pi*r2) infinitesimal area = dtheta*r1*dphi*r2
Volume = (2*Pi*r1)*(Pi*r2*r2) infinitesimal volume = dtheta*r1*dphi*r2*dr2
Equation (r1-sqrt(x^2+y^2))^2 + z^2 = r2^2
r2, x, y, z mapped to r1, theta, phi (r2 taken as constant)
theta = arctan(y/x)
phi = arccos(z/r2)
r1 = x/cos(theta) - r2*sin(phi) or
r1 = y/sin(theta) - r2*sin(phi) no divide by zero
r1, x, y, z mapped to r2, theta, phi (r1 taken as constant)
theta = arctan(y/x) fix angle by quadrant
x1 = r1*cos(theta)
y1 = r1*sin(theta)
phi = arctan(sqrt((x-x1)^2+(y-y1)^2)/z) fix by quadrant
r2 = sqrt((x-x1)^2+(y-y1)^2+z^2)
PDE for testing: r1 constant, r2 is r, theta is t, phi is p
dU^2(r1,r2,t,p)/dr2^2 + dU^2(r1,r2,t,p)/dt^2 +
dU^2(r1,r2,t,p)/dp^2 = f(r1,r2,t,p)
U(r,t,p):=r*r*(1+sin(t))*(1+cos(p));
2
U(r, t, p) := r (1 + sin(t)) (1 + cos(p))
Urr(r,t,p):=diff(diff(U(r,t.p),r),r);
Urr(r, t, p) := D[1, 1](U)(r, t . p)
Urr(r,t,p):=diff(diff(U(r,t,p),r),r);
Urr(r, t, p) := 2 (1 + sin(t)) (1 + cos(p))
Utt(r,t,p):=diff(diff(U(r,t,p),t),t);
2
Utt(r, t, p) := -r sin(t) (1 + cos(p))
Upp(r,t,p):=diff(diff(U(r,t,p),p),p);
2
Upp(r, t, p) := -r (1 + sin(t)) cos(p)
f(r,t,p):=Urr(r,t,p)+Utt(r,t,p)+Upp(r,t,p);
2
f(r, t, p) := 2 (1 + sin(t)) (1 + cos(p)) - r sin(t) (1 + cos(p))
2
- r (1 + sin(t)) cos(p)
simplify(f(r,t,p));
2 2
2 + 2 cos(p) + 2 sin(t) + 2 sin(t) cos(p) - r sin(t) - 2 r sin(t) cos(p)
2
- r cos(p)
f(r2,t,p) =
2.0*(1.0 + cos(p) + sin(t) + sin(t)*cos(p)) -
r2*r2*(cos(p) + sin(t) + 2.0*sin(t)*cos(p))
Ub(r2,t,p):=r2*r2*(1.0+sin(t))*(1.0+cos(p)); Dirichlet boundary
Another view of refinement
Toroid center at 0,0,0 can be translated and rotated
r1, r2, theta, phi mapped to x,y,z
x = (r1+r2*sin(phi))*cos(theta)
y = (r1+r2*sin(phi))*sin(theta)
z = r2 * cos(phi)
0 ≤ theta ≤ 2Pi 0 ≤ phi ≤ 2Pi 0 < r2 < r1
Area = (2*Pi*r1)*(2*Pi*r2) infinitesimal area = dtheta*r1*dphi*r2
Volume = (2*Pi*r1)*(Pi*r2*r2) infinitesimal volume = dtheta*r1*dphi*r2*dr2
Equation (r1-sqrt(x^2+y^2))^2 + z^2 = r2^2
r2, x, y, z mapped to r1, theta, phi (r2 taken as constant)
theta = arctan(y/x)
phi = arccos(z/r2)
r1 = x/cos(theta) - r2*sin(phi) or
r1 = y/sin(theta) - r2*sin(phi) no divide by zero
r1, x, y, z mapped to r2, theta, phi (r1 taken as constant)
theta = arctan(y/x) fix angle by quadrant
x1 = r1*cos(theta)
y1 = r1*sin(theta)
phi = arctan(sqrt((x-x1)^2+(y-y1)^2)/z) fix by quadrant
r2 = sqrt((x-x1)^2+(y-y1)^2+z^2)
PDE for testing: r1 constant, r2 is r, theta is t, phi is p
dU^2(r1,r2,t,p)/dr2^2 + dU^2(r1,r2,t,p)/dt^2 +
dU^2(r1,r2,t,p)/dp^2 = f(r1,r2,t,p)
U(r,t,p):=r*r*(1+sin(t))*(1+cos(p));
2
U(r, t, p) := r (1 + sin(t)) (1 + cos(p))
Urr(r,t,p):=diff(diff(U(r,t.p),r),r);
Urr(r, t, p) := D[1, 1](U)(r, t . p)
Urr(r,t,p):=diff(diff(U(r,t,p),r),r);
Urr(r, t, p) := 2 (1 + sin(t)) (1 + cos(p))
Utt(r,t,p):=diff(diff(U(r,t,p),t),t);
2
Utt(r, t, p) := -r sin(t) (1 + cos(p))
Upp(r,t,p):=diff(diff(U(r,t,p),p),p);
2
Upp(r, t, p) := -r (1 + sin(t)) cos(p)
f(r,t,p):=Urr(r,t,p)+Utt(r,t,p)+Upp(r,t,p);
2
f(r, t, p) := 2 (1 + sin(t)) (1 + cos(p)) - r sin(t) (1 + cos(p))
2
- r (1 + sin(t)) cos(p)
simplify(f(r,t,p));
2 2
2 + 2 cos(p) + 2 sin(t) + 2 sin(t) cos(p) - r sin(t) - 2 r sin(t) cos(p)
2
- r cos(p)
f(r2,t,p) =
2.0*(1.0 + cos(p) + sin(t) + sin(t)*cos(p)) -
r2*r2*(cos(p) + sin(t) + 2.0*sin(t)*cos(p))
Ub(r2,t,p):=r2*r2*(1.0+sin(t))*(1.0+cos(p)); Dirichlet boundary
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation

 First refinement
First refinement
 Another view of refinement
Toroid center at 0,0,0 can be translated and rotated
r1, r2, theta, phi mapped to x,y,z
x = (r1+r2*sin(phi))*cos(theta)
y = (r1+r2*sin(phi))*sin(theta)
z = r2 * cos(phi)
0 ≤ theta ≤ 2Pi 0 ≤ phi ≤ 2Pi 0 < r2 < r1
Area = (2*Pi*r1)*(2*Pi*r2) infinitesimal area = dtheta*r1*dphi*r2
Volume = (2*Pi*r1)*(Pi*r2*r2) infinitesimal volume = dtheta*r1*dphi*r2*dr2
Equation (r1-sqrt(x^2+y^2))^2 + z^2 = r2^2
r2, x, y, z mapped to r1, theta, phi (r2 taken as constant)
theta = arctan(y/x)
phi = arccos(z/r2)
r1 = x/cos(theta) - r2*sin(phi) or
r1 = y/sin(theta) - r2*sin(phi) no divide by zero
r1, x, y, z mapped to r2, theta, phi (r1 taken as constant)
theta = arctan(y/x) fix angle by quadrant
x1 = r1*cos(theta)
y1 = r1*sin(theta)
phi = arctan(sqrt((x-x1)^2+(y-y1)^2)/z) fix by quadrant
r2 = sqrt((x-x1)^2+(y-y1)^2+z^2)
PDE for testing: r1 constant, r2 is r, theta is t, phi is p
dU^2(r1,r2,t,p)/dr2^2 + dU^2(r1,r2,t,p)/dt^2 +
dU^2(r1,r2,t,p)/dp^2 = f(r1,r2,t,p)
U(r,t,p):=r*r*(1+sin(t))*(1+cos(p));
2
U(r, t, p) := r (1 + sin(t)) (1 + cos(p))
Urr(r,t,p):=diff(diff(U(r,t.p),r),r);
Urr(r, t, p) := D[1, 1](U)(r, t . p)
Urr(r,t,p):=diff(diff(U(r,t,p),r),r);
Urr(r, t, p) := 2 (1 + sin(t)) (1 + cos(p))
Utt(r,t,p):=diff(diff(U(r,t,p),t),t);
2
Utt(r, t, p) := -r sin(t) (1 + cos(p))
Upp(r,t,p):=diff(diff(U(r,t,p),p),p);
2
Upp(r, t, p) := -r (1 + sin(t)) cos(p)
f(r,t,p):=Urr(r,t,p)+Utt(r,t,p)+Upp(r,t,p);
2
f(r, t, p) := 2 (1 + sin(t)) (1 + cos(p)) - r sin(t) (1 + cos(p))
2
- r (1 + sin(t)) cos(p)
simplify(f(r,t,p));
2 2
2 + 2 cos(p) + 2 sin(t) + 2 sin(t) cos(p) - r sin(t) - 2 r sin(t) cos(p)
2
- r cos(p)
f(r2,t,p) =
2.0*(1.0 + cos(p) + sin(t) + sin(t)*cos(p)) -
r2*r2*(cos(p) + sin(t) + 2.0*sin(t)*cos(p))
Ub(r2,t,p):=r2*r2*(1.0+sin(t))*(1.0+cos(p)); Dirichlet boundary
Another view of refinement
Toroid center at 0,0,0 can be translated and rotated
r1, r2, theta, phi mapped to x,y,z
x = (r1+r2*sin(phi))*cos(theta)
y = (r1+r2*sin(phi))*sin(theta)
z = r2 * cos(phi)
0 ≤ theta ≤ 2Pi 0 ≤ phi ≤ 2Pi 0 < r2 < r1
Area = (2*Pi*r1)*(2*Pi*r2) infinitesimal area = dtheta*r1*dphi*r2
Volume = (2*Pi*r1)*(Pi*r2*r2) infinitesimal volume = dtheta*r1*dphi*r2*dr2
Equation (r1-sqrt(x^2+y^2))^2 + z^2 = r2^2
r2, x, y, z mapped to r1, theta, phi (r2 taken as constant)
theta = arctan(y/x)
phi = arccos(z/r2)
r1 = x/cos(theta) - r2*sin(phi) or
r1 = y/sin(theta) - r2*sin(phi) no divide by zero
r1, x, y, z mapped to r2, theta, phi (r1 taken as constant)
theta = arctan(y/x) fix angle by quadrant
x1 = r1*cos(theta)
y1 = r1*sin(theta)
phi = arctan(sqrt((x-x1)^2+(y-y1)^2)/z) fix by quadrant
r2 = sqrt((x-x1)^2+(y-y1)^2+z^2)
PDE for testing: r1 constant, r2 is r, theta is t, phi is p
dU^2(r1,r2,t,p)/dr2^2 + dU^2(r1,r2,t,p)/dt^2 +
dU^2(r1,r2,t,p)/dp^2 = f(r1,r2,t,p)
U(r,t,p):=r*r*(1+sin(t))*(1+cos(p));
2
U(r, t, p) := r (1 + sin(t)) (1 + cos(p))
Urr(r,t,p):=diff(diff(U(r,t.p),r),r);
Urr(r, t, p) := D[1, 1](U)(r, t . p)
Urr(r,t,p):=diff(diff(U(r,t,p),r),r);
Urr(r, t, p) := 2 (1 + sin(t)) (1 + cos(p))
Utt(r,t,p):=diff(diff(U(r,t,p),t),t);
2
Utt(r, t, p) := -r sin(t) (1 + cos(p))
Upp(r,t,p):=diff(diff(U(r,t,p),p),p);
2
Upp(r, t, p) := -r (1 + sin(t)) cos(p)
f(r,t,p):=Urr(r,t,p)+Utt(r,t,p)+Upp(r,t,p);
2
f(r, t, p) := 2 (1 + sin(t)) (1 + cos(p)) - r sin(t) (1 + cos(p))
2
- r (1 + sin(t)) cos(p)
simplify(f(r,t,p));
2 2
2 + 2 cos(p) + 2 sin(t) + 2 sin(t) cos(p) - r sin(t) - 2 r sin(t) cos(p)
2
- r cos(p)
f(r2,t,p) =
2.0*(1.0 + cos(p) + sin(t) + sin(t)*cos(p)) -
r2*r2*(cos(p) + sin(t) + 2.0*sin(t)*cos(p))
Ub(r2,t,p):=r2*r2*(1.0+sin(t))*(1.0+cos(p)); Dirichlet boundary