<- previous index next ->
Just extending fourth order PDE in four dimensions, to six dimensions
Desired solution is U(v,w,x,y,z,t), given PDE:
∇4U + 2 ∇2U + 6 U = 0
∂4U(v,w,x,y,z,t)/∂v4 + ∂4U(v,w,x,y,z,t)/∂w4 +
∂4U(v,w,x,y,z,t)/∂x4 + ∂4U(v,w,x,y,z,t)/∂y4 +
∂4U(v,w,x,y,z,t)/∂z4 + ∂4U(v,w,x,y,z,t)/∂t4 +
2 ∂2U(v,w,x,y,z,t)/∂v2 + 2 ∂2U(v,w,x,y,z,t)/∂w2 +
2 ∂2U(v,w,x,y,z,t)/∂x2 + 2 ∂2U(v,w,x,y,z,t)/∂y2 +
2 ∂2U(v,w,x,y,z,t)/∂z2 + 2 ∂2U(v,w,x,y,z,t)/∂t2 +
6 U(v,w,x,y,z,t) = 0
6D cubes and spheres
faces.c program
faces.out Data on 2D to 6D
test_faces.c program
test_faces.out sphere data
faces.java program
faces_java.out Data on 2D to 6D
test_faces.java program
test_faces_java.out sphere equations test
Test a fourth order PDE in six dimensions.
∇4U + 2 ∇2U + 6 U = 0
pde46h_eq.adb extended pde44h_eq.adb
pde46h_eq_ada.out verification output
∇4U + 2 ∇2U + 6 U = 0
pde46h_eq.c
pde46h_eq_c.out verification output
∇4U + 2 ∇2U + 6 U = 0
pde46h_eq.f90
pde46h_eq_f90.out verification output
∇4U + 2 ∇2U + 6 U = 0
pde46h_eq.java
pde46h_eq_java.out verification output
 Plotted with plot6d_gl.c, stopped on one of the moving output
pde46h_eq_java.dat data written for plot
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = exp(x+y+t*z+u+v) six independent variables, 4th order
pde64eb_eq.c testing source code
pde64eb_eq_c.out verification output
d6p4eb.mw Maple test generation
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = sin(x*u+y*v+z+t) six independent variables, 4th order
pde64sb_eq.c testing source code
pde64sb_eq_c.out verification output
d6p4sb.mw Maple test generation
d6p4sb_rhs.jpg RHS
Plotted with plot6d_gl.c, stopped on one of the moving output
pde46h_eq_java.dat data written for plot
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = exp(x+y+t*z+u+v) six independent variables, 4th order
pde64eb_eq.c testing source code
pde64eb_eq_c.out verification output
d6p4eb.mw Maple test generation
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = sin(x*u+y*v+z+t) six independent variables, 4th order
pde64sb_eq.c testing source code
pde64sb_eq_c.out verification output
d6p4sb.mw Maple test generation
d6p4sb_rhs.jpg RHS
Plotting solution against 6D independent variables
Designed for interactive changing of variables plotted and variables values.
pot6d_gl.c plot program
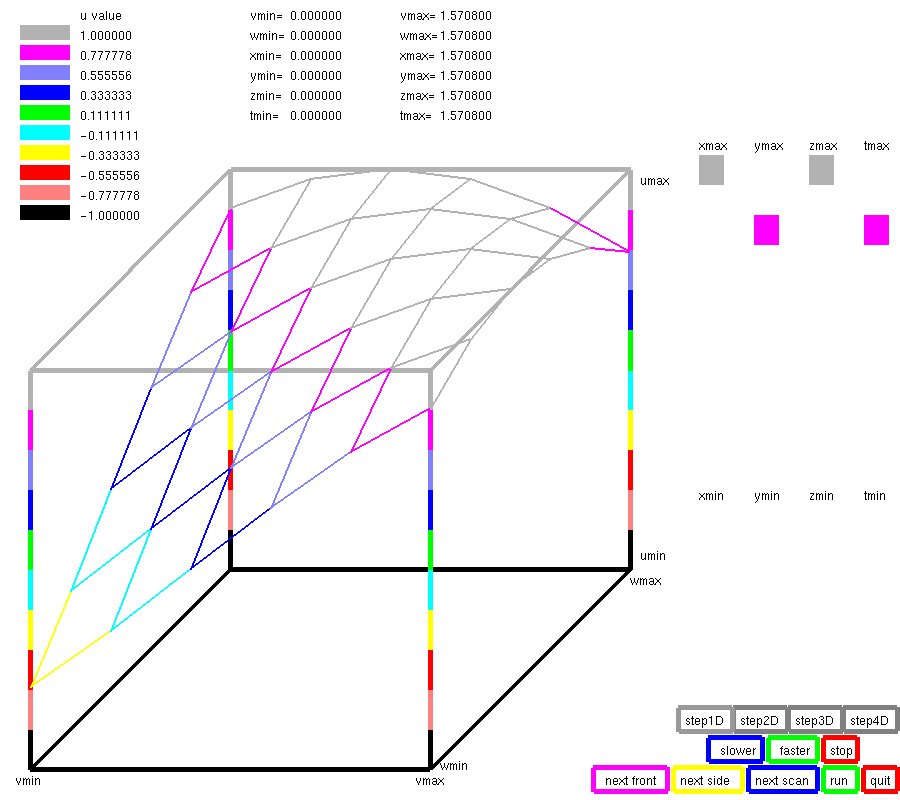
With a small change, we obtain a nonuniform refinement
Now we use "nuderiv" rather than "rderiv" that can use
nonuniform and different grids in each dimension.
Test a fourth order PDE in six dimensions with nonuniform refinement.
∇4U + 2 ∇2U + 6 U = 0
pde46h_nu.adb extended pde46h_eq.adb
pde46h_nu_ada.out verification output
∇4U + 2 ∇2U + 6 U = 0
pde46h_nu.java
pde46h_nu_java.out verification output
∇4U + 2 ∇2U + 6 U = 0
pde46h_nu.c
pde46h_nu_c.out verification output
Plotting solution against 6D independent variables
Designed for interactive changing of variables plotted and variables values.
pot6d_gl.c plot program
 pde46h_nu_ada.jpg
pde46h_nu_ada.jpg
Least Square Fit 6 independent variables up to sixth power
lsfit.ads Least Square Fit 6D 6P
lsfit.adb Least Square Fit 6D 6P
test_lsfit6.adb test program
test_lsfit6_ada.out test results
Some programs above also need
simeq.f90 solve simultaneous equations
deriv.f90 compute numerical derivatives
array3d.ads 3D arrays
array4d.ads 4D arrays
array5d.ads 5D arrays
array6d.ads 6D arrays
real_arrays.ads 2D arrays and operations
real_arrays.adb 2D arrays and operations
integer_arrays.ads 2D arrays and operations
integer_arrays.adb 2D arrays and operations
You won't find many free or commercial 5D and 6D PDE packages
many lesser problems have many opensource and commercial packages
en.wikipedia.org/wiki/list_of_finite_element_software_packages
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation
 Plotted with plot6d_gl.c, stopped on one of the moving output
pde46h_eq_java.dat data written for plot
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = exp(x+y+t*z+u+v) six independent variables, 4th order
pde64eb_eq.c testing source code
pde64eb_eq_c.out verification output
d6p4eb.mw Maple test generation
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = sin(x*u+y*v+z+t) six independent variables, 4th order
pde64sb_eq.c testing source code
pde64sb_eq_c.out verification output
d6p4sb.mw Maple test generation
d6p4sb_rhs.jpg RHS
Plotted with plot6d_gl.c, stopped on one of the moving output
pde46h_eq_java.dat data written for plot
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = exp(x+y+t*z+u+v) six independent variables, 4th order
pde64eb_eq.c testing source code
pde64eb_eq_c.out verification output
d6p4eb.mw Maple test generation
∇4P + 2 ∇2P = f(x,y,z,t,u,v)
Solving for P = sin(x*u+y*v+z+t) six independent variables, 4th order
pde64sb_eq.c testing source code
pde64sb_eq_c.out verification output
d6p4sb.mw Maple test generation
d6p4sb_rhs.jpg RHS

 pde46h_nu_ada.jpg
pde46h_nu_ada.jpg