<- previous index next ->
One version of Navier Stokes equation


 Each term above has units of length over time squared, acceleration,
in meters per second squared. u is the three component velocity
vector, each component in meters per second, ρ is the fluid density
in kilograms per cubic meter, p is the pressure in newtons per square meter,
μ is the dynamic viscosity newton seconds per square meter.
X is externally applied acceleration, F/m, newtons per kilogram.
Another representation of Navier Stokes equation, multiplying the
above equation by ρ, yields terms that are force per unit volume,
newtons per cubic meter. del ∇ is the differential operator,
gradient. v is the velocity vector. b is externally applied acceleration.
Each term above has units of length over time squared, acceleration,
in meters per second squared. u is the three component velocity
vector, each component in meters per second, ρ is the fluid density
in kilograms per cubic meter, p is the pressure in newtons per square meter,
μ is the dynamic viscosity newton seconds per square meter.
X is externally applied acceleration, F/m, newtons per kilogram.
Another representation of Navier Stokes equation, multiplying the
above equation by ρ, yields terms that are force per unit volume,
newtons per cubic meter. del ∇ is the differential operator,
gradient. v is the velocity vector. b is externally applied acceleration.
 navier_gl.txt notes
navier_gl.c work in progress
navier_gl.out output attempt
navier_gl.txt notes
navier_gl.c work in progress
navier_gl.out output attempt
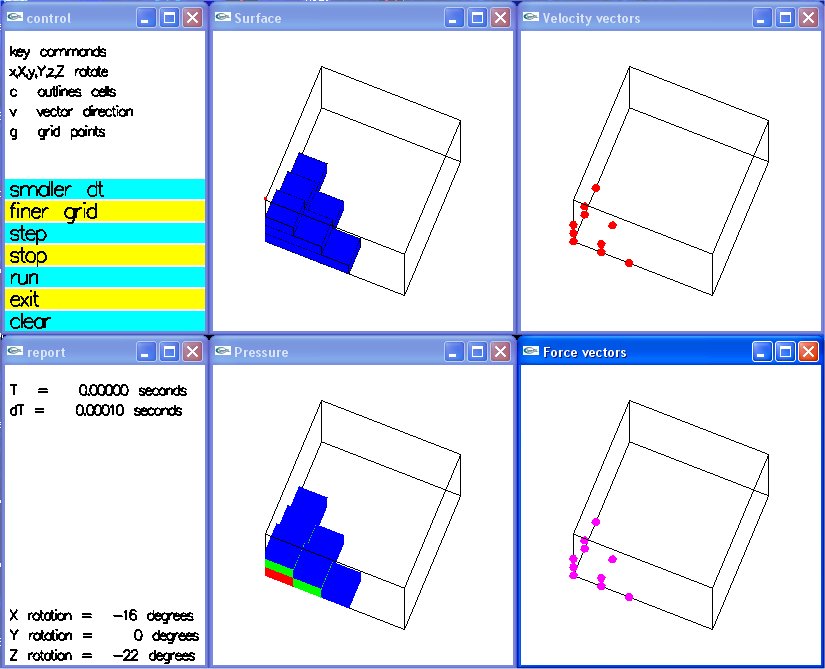 Some notes for your consideration:
1) You are expected to be intelligent enough to know the practical
limitations of equations that are given to you. When you develop
the equations, you must take into account practical limitations.
Many scholarly textbooks on differential equations make the
statement that a differential equation describing the physical
world is an approximation of what will actually happen. If you
keep stretching a spring using F = k x, the equation only
applies until the spring breaks.
2) We use the statement that "mass is conserved" in many physical
equations. Understand that the limits, usually unstated, are
"in a closed system and with no E = M C^2" Typically fluid equations
do not account for evaporation or fluid loss do to leaks or spillage.
The equations assume an absolutely closed system.
3) We use, as a fact "energy is conserved" in many physical equations.
Energy may take many forms and energy is easily converted from one
form to another and may not be taken into account by a specific equation.
For example, potential energy, a given mass at a given height, may
be released and potential energy is converted to kinetic energy.
Then, splat, the mass hits the ground in an inelastic collision and
has zero potential and zero kinetic energy. Most of the energy is
converted to heat energy with the possible conversion to some
chemical energy and some electrical energy.
Understand that heat and electrical energy can take the form
of radiation and leave what you are considering a "closed system."
4) Momentum is not conserved during a non elastic collision!
Fortunately, molecules of most fluids do not stick very often.
Surface tension must be taken into account when the fluid has
a surface open to the atmosphere. Capillary action affect must
be taken into account when a fluid "wets" a vertical surface.
5) When considering an infinitesimal volume, for example a cube in
a Cartesian measurement system. We generally take z to be the
vertical axis, meaning along a gravitational force line. We
consider a non compressible fluid in this cube with side s, to have
pressure applied to all six faces. Several cases are possible:
a) The fluid is stationary, what are the pressure on each face?
We define pressure as positive force divided by area into the cube.
aa) The cube of fluid has the same fluid on all sides.
Because of gravity, not all faces have the same pressure.
Given pressure P on the more positive X face, there must
be the same force P on the more negative X face else
the cube would accelerate and move. The pressure on both
Y faces must be the same P else fluid would move into or
out of the cube in the Y direction.
But, we are making an assumption that the pressure is constant
all over the X and Y faces yet this is an approximation. The
fluid has density and thus the mass is density times volume.
Mass is attracted by gravity. We can reasonably assume the force
of gravity does not change enough to be considered for the height
s, of our infinitesimal cube. Yet the pressure on the more positive
Z face must be considered different from the pressure on
the more negative Z face. Gravity puts a force of mass times
the gravitational constant g in the negative Z direction
on the fluid in the cube. With g taken as a constant, the
force is linear in the Z direction, thus the pressure P
on the X and Y faces is actually the pressure at the center
of each face. The pressure on the top, most positive Z face
is P - 1/2 rho * s * g and the pressure on the bottom,
most negative Z face is P + 1/2 rho * s * g. Pressure must
increase as depth increases.
ab) One or more face is against an immovable wall.
Same as aa)
b) The fluid is moving at a constant velocity.
ba) The cube of fluid has the same velocity as fluid on all sides.
Same as aa)
bb) The fluid against some face is moving at a different velocity.
Now we can not ignore viscosity. Viscosity is essentially a
measure of sliding resistance between the fluids at the faces
of two adjacent infinitesimal cubes.
c) The fluid is accelerating.
All of the above must be taken into account with the addition
of F = m a applied to the center of mass of the cube.
Consider the X direction with pressure P1 on the most negative
X face and a smaller P2 on the most positive X face. We can
apply the force (P1 - P2)*s^2 in the positive X direction to
the center of mass. Differences the pressure on Y faces are
independently applied to the Y direction. Use caution in
the Z direction, subtracting the difference in pressure due
to gravity because this does not impart an acceleration on
the center of mass when the infinitesimal cube has fluid or
an immovable surface under the cube.
It may be too late, but, don't panic, this was a small part of
Computational Fluid Dynamics, CFD. CFD is a large area and modeling
includes supersonic flight in complex scenarios.
More references:
navier_stokes.equation
navier_stokes_2d.equation
navier.equations breif
navier_fem.pdf technical paper
metric_units.txt metric definitions
also used in lecture 22 space satellite problem
air_prop.txt air properties
physics1.txt equations
convert_metric.pdf conversion
units.txt units definitions
Some notes for your consideration:
1) You are expected to be intelligent enough to know the practical
limitations of equations that are given to you. When you develop
the equations, you must take into account practical limitations.
Many scholarly textbooks on differential equations make the
statement that a differential equation describing the physical
world is an approximation of what will actually happen. If you
keep stretching a spring using F = k x, the equation only
applies until the spring breaks.
2) We use the statement that "mass is conserved" in many physical
equations. Understand that the limits, usually unstated, are
"in a closed system and with no E = M C^2" Typically fluid equations
do not account for evaporation or fluid loss do to leaks or spillage.
The equations assume an absolutely closed system.
3) We use, as a fact "energy is conserved" in many physical equations.
Energy may take many forms and energy is easily converted from one
form to another and may not be taken into account by a specific equation.
For example, potential energy, a given mass at a given height, may
be released and potential energy is converted to kinetic energy.
Then, splat, the mass hits the ground in an inelastic collision and
has zero potential and zero kinetic energy. Most of the energy is
converted to heat energy with the possible conversion to some
chemical energy and some electrical energy.
Understand that heat and electrical energy can take the form
of radiation and leave what you are considering a "closed system."
4) Momentum is not conserved during a non elastic collision!
Fortunately, molecules of most fluids do not stick very often.
Surface tension must be taken into account when the fluid has
a surface open to the atmosphere. Capillary action affect must
be taken into account when a fluid "wets" a vertical surface.
5) When considering an infinitesimal volume, for example a cube in
a Cartesian measurement system. We generally take z to be the
vertical axis, meaning along a gravitational force line. We
consider a non compressible fluid in this cube with side s, to have
pressure applied to all six faces. Several cases are possible:
a) The fluid is stationary, what are the pressure on each face?
We define pressure as positive force divided by area into the cube.
aa) The cube of fluid has the same fluid on all sides.
Because of gravity, not all faces have the same pressure.
Given pressure P on the more positive X face, there must
be the same force P on the more negative X face else
the cube would accelerate and move. The pressure on both
Y faces must be the same P else fluid would move into or
out of the cube in the Y direction.
But, we are making an assumption that the pressure is constant
all over the X and Y faces yet this is an approximation. The
fluid has density and thus the mass is density times volume.
Mass is attracted by gravity. We can reasonably assume the force
of gravity does not change enough to be considered for the height
s, of our infinitesimal cube. Yet the pressure on the more positive
Z face must be considered different from the pressure on
the more negative Z face. Gravity puts a force of mass times
the gravitational constant g in the negative Z direction
on the fluid in the cube. With g taken as a constant, the
force is linear in the Z direction, thus the pressure P
on the X and Y faces is actually the pressure at the center
of each face. The pressure on the top, most positive Z face
is P - 1/2 rho * s * g and the pressure on the bottom,
most negative Z face is P + 1/2 rho * s * g. Pressure must
increase as depth increases.
ab) One or more face is against an immovable wall.
Same as aa)
b) The fluid is moving at a constant velocity.
ba) The cube of fluid has the same velocity as fluid on all sides.
Same as aa)
bb) The fluid against some face is moving at a different velocity.
Now we can not ignore viscosity. Viscosity is essentially a
measure of sliding resistance between the fluids at the faces
of two adjacent infinitesimal cubes.
c) The fluid is accelerating.
All of the above must be taken into account with the addition
of F = m a applied to the center of mass of the cube.
Consider the X direction with pressure P1 on the most negative
X face and a smaller P2 on the most positive X face. We can
apply the force (P1 - P2)*s^2 in the positive X direction to
the center of mass. Differences the pressure on Y faces are
independently applied to the Y direction. Use caution in
the Z direction, subtracting the difference in pressure due
to gravity because this does not impart an acceleration on
the center of mass when the infinitesimal cube has fluid or
an immovable surface under the cube.
It may be too late, but, don't panic, this was a small part of
Computational Fluid Dynamics, CFD. CFD is a large area and modeling
includes supersonic flight in complex scenarios.
More references:
navier_stokes.equation
navier_stokes_2d.equation
navier.equations breif
navier_fem.pdf technical paper
metric_units.txt metric definitions
also used in lecture 22 space satellite problem
air_prop.txt air properties
physics1.txt equations
convert_metric.pdf conversion
units.txt units definitions
<- previous index next ->
-
CMSC 455 home page
-
Syllabus - class dates and subjects, homework dates, reading assignments
-
Homework assignments - the details
-
Projects -
-
Partial Lecture Notes, one per WEB page
-
Partial Lecture Notes, one big page for printing
-
Downloadable samples, source and executables
-
Some brief notes on Matlab
-
Some brief notes on Python
-
Some brief notes on Fortran 95
-
Some brief notes on Ada 95
-
An Ada math library (gnatmath95)
-
Finite difference approximations for derivatives
-
MATLAB examples, some ODE, some PDE
-
parallel threads examples
-
Reference pages on Taylor series, identities,
coordinate systems, differential operators
-
selected news related to numerical computation


 Each term above has units of length over time squared, acceleration,
in meters per second squared. u is the three component velocity
vector, each component in meters per second, ρ is the fluid density
in kilograms per cubic meter, p is the pressure in newtons per square meter,
μ is the dynamic viscosity newton seconds per square meter.
X is externally applied acceleration, F/m, newtons per kilogram.
Another representation of Navier Stokes equation, multiplying the
above equation by ρ, yields terms that are force per unit volume,
newtons per cubic meter. del ∇ is the differential operator,
gradient. v is the velocity vector.
Each term above has units of length over time squared, acceleration,
in meters per second squared. u is the three component velocity
vector, each component in meters per second, ρ is the fluid density
in kilograms per cubic meter, p is the pressure in newtons per square meter,
μ is the dynamic viscosity newton seconds per square meter.
X is externally applied acceleration, F/m, newtons per kilogram.
Another representation of Navier Stokes equation, multiplying the
above equation by ρ, yields terms that are force per unit volume,
newtons per cubic meter. del ∇ is the differential operator,
gradient. v is the velocity vector.  navier_gl.txt notes
navier_gl.c work in progress
navier_gl.out output attempt
navier_gl.txt notes
navier_gl.c work in progress
navier_gl.out output attempt
 Some notes for your consideration:
1) You are expected to be intelligent enough to know the practical
limitations of equations that are given to you. When you develop
the equations, you must take into account practical limitations.
Many scholarly textbooks on differential equations make the
statement that a differential equation describing the physical
world is an approximation of what will actually happen. If you
keep stretching a spring using F = k x, the equation only
applies until the spring breaks.
2) We use the statement that "mass is conserved" in many physical
equations. Understand that the limits, usually unstated, are
"in a closed system and with no E = M C^2" Typically fluid equations
do not account for evaporation or fluid loss do to leaks or spillage.
The equations assume an absolutely closed system.
3) We use, as a fact "energy is conserved" in many physical equations.
Energy may take many forms and energy is easily converted from one
form to another and may not be taken into account by a specific equation.
For example, potential energy, a given mass at a given height, may
be released and potential energy is converted to kinetic energy.
Then, splat, the mass hits the ground in an inelastic collision and
has zero potential and zero kinetic energy. Most of the energy is
converted to heat energy with the possible conversion to some
chemical energy and some electrical energy.
Understand that heat and electrical energy can take the form
of radiation and leave what you are considering a "closed system."
4) Momentum is not conserved during a non elastic collision!
Fortunately, molecules of most fluids do not stick very often.
Surface tension must be taken into account when the fluid has
a surface open to the atmosphere. Capillary action affect must
be taken into account when a fluid "wets" a vertical surface.
5) When considering an infinitesimal volume, for example a cube in
a Cartesian measurement system. We generally take z to be the
vertical axis, meaning along a gravitational force line. We
consider a non compressible fluid in this cube with side s, to have
pressure applied to all six faces. Several cases are possible:
a) The fluid is stationary, what are the pressure on each face?
We define pressure as positive force divided by area into the cube.
aa) The cube of fluid has the same fluid on all sides.
Because of gravity, not all faces have the same pressure.
Given pressure P on the more positive X face, there must
be the same force P on the more negative X face else
the cube would accelerate and move. The pressure on both
Y faces must be the same P else fluid would move into or
out of the cube in the Y direction.
But, we are making an assumption that the pressure is constant
all over the X and Y faces yet this is an approximation. The
fluid has density and thus the mass is density times volume.
Mass is attracted by gravity. We can reasonably assume the force
of gravity does not change enough to be considered for the height
s, of our infinitesimal cube. Yet the pressure on the more positive
Z face must be considered different from the pressure on
the more negative Z face. Gravity puts a force of mass times
the gravitational constant g in the negative Z direction
on the fluid in the cube. With g taken as a constant, the
force is linear in the Z direction, thus the pressure P
on the X and Y faces is actually the pressure at the center
of each face. The pressure on the top, most positive Z face
is P - 1/2 rho * s * g and the pressure on the bottom,
most negative Z face is P + 1/2 rho * s * g. Pressure must
increase as depth increases.
ab) One or more face is against an immovable wall.
Same as aa)
b) The fluid is moving at a constant velocity.
ba) The cube of fluid has the same velocity as fluid on all sides.
Same as aa)
bb) The fluid against some face is moving at a different velocity.
Now we can not ignore viscosity. Viscosity is essentially a
measure of sliding resistance between the fluids at the faces
of two adjacent infinitesimal cubes.
c) The fluid is accelerating.
All of the above must be taken into account with the addition
of F = m a applied to the center of mass of the cube.
Consider the X direction with pressure P1 on the most negative
X face and a smaller P2 on the most positive X face. We can
apply the force (P1 - P2)*s^2 in the positive X direction to
the center of mass. Differences the pressure on Y faces are
independently applied to the Y direction. Use caution in
the Z direction, subtracting the difference in pressure due
to gravity because this does not impart an acceleration on
the center of mass when the infinitesimal cube has fluid or
an immovable surface under the cube.
It may be too late, but, don't panic, this was a small part of
Computational Fluid Dynamics, CFD. CFD is a large area and modeling
includes supersonic flight in complex scenarios.
More references:
navier_stokes.equation
navier_stokes_2d.equation
navier.equations breif
navier_fem.pdf technical paper
metric_units.txt metric definitions
also used in lecture 22 space satellite problem
air_prop.txt air properties
physics1.txt equations
convert_metric.pdf conversion
units.txt units definitions
Some notes for your consideration:
1) You are expected to be intelligent enough to know the practical
limitations of equations that are given to you. When you develop
the equations, you must take into account practical limitations.
Many scholarly textbooks on differential equations make the
statement that a differential equation describing the physical
world is an approximation of what will actually happen. If you
keep stretching a spring using F = k x, the equation only
applies until the spring breaks.
2) We use the statement that "mass is conserved" in many physical
equations. Understand that the limits, usually unstated, are
"in a closed system and with no E = M C^2" Typically fluid equations
do not account for evaporation or fluid loss do to leaks or spillage.
The equations assume an absolutely closed system.
3) We use, as a fact "energy is conserved" in many physical equations.
Energy may take many forms and energy is easily converted from one
form to another and may not be taken into account by a specific equation.
For example, potential energy, a given mass at a given height, may
be released and potential energy is converted to kinetic energy.
Then, splat, the mass hits the ground in an inelastic collision and
has zero potential and zero kinetic energy. Most of the energy is
converted to heat energy with the possible conversion to some
chemical energy and some electrical energy.
Understand that heat and electrical energy can take the form
of radiation and leave what you are considering a "closed system."
4) Momentum is not conserved during a non elastic collision!
Fortunately, molecules of most fluids do not stick very often.
Surface tension must be taken into account when the fluid has
a surface open to the atmosphere. Capillary action affect must
be taken into account when a fluid "wets" a vertical surface.
5) When considering an infinitesimal volume, for example a cube in
a Cartesian measurement system. We generally take z to be the
vertical axis, meaning along a gravitational force line. We
consider a non compressible fluid in this cube with side s, to have
pressure applied to all six faces. Several cases are possible:
a) The fluid is stationary, what are the pressure on each face?
We define pressure as positive force divided by area into the cube.
aa) The cube of fluid has the same fluid on all sides.
Because of gravity, not all faces have the same pressure.
Given pressure P on the more positive X face, there must
be the same force P on the more negative X face else
the cube would accelerate and move. The pressure on both
Y faces must be the same P else fluid would move into or
out of the cube in the Y direction.
But, we are making an assumption that the pressure is constant
all over the X and Y faces yet this is an approximation. The
fluid has density and thus the mass is density times volume.
Mass is attracted by gravity. We can reasonably assume the force
of gravity does not change enough to be considered for the height
s, of our infinitesimal cube. Yet the pressure on the more positive
Z face must be considered different from the pressure on
the more negative Z face. Gravity puts a force of mass times
the gravitational constant g in the negative Z direction
on the fluid in the cube. With g taken as a constant, the
force is linear in the Z direction, thus the pressure P
on the X and Y faces is actually the pressure at the center
of each face. The pressure on the top, most positive Z face
is P - 1/2 rho * s * g and the pressure on the bottom,
most negative Z face is P + 1/2 rho * s * g. Pressure must
increase as depth increases.
ab) One or more face is against an immovable wall.
Same as aa)
b) The fluid is moving at a constant velocity.
ba) The cube of fluid has the same velocity as fluid on all sides.
Same as aa)
bb) The fluid against some face is moving at a different velocity.
Now we can not ignore viscosity. Viscosity is essentially a
measure of sliding resistance between the fluids at the faces
of two adjacent infinitesimal cubes.
c) The fluid is accelerating.
All of the above must be taken into account with the addition
of F = m a applied to the center of mass of the cube.
Consider the X direction with pressure P1 on the most negative
X face and a smaller P2 on the most positive X face. We can
apply the force (P1 - P2)*s^2 in the positive X direction to
the center of mass. Differences the pressure on Y faces are
independently applied to the Y direction. Use caution in
the Z direction, subtracting the difference in pressure due
to gravity because this does not impart an acceleration on
the center of mass when the infinitesimal cube has fluid or
an immovable surface under the cube.
It may be too late, but, don't panic, this was a small part of
Computational Fluid Dynamics, CFD. CFD is a large area and modeling
includes supersonic flight in complex scenarios.
More references:
navier_stokes.equation
navier_stokes_2d.equation
navier.equations breif
navier_fem.pdf technical paper
metric_units.txt metric definitions
also used in lecture 22 space satellite problem
air_prop.txt air properties
physics1.txt equations
convert_metric.pdf conversion
units.txt units definitions