<- previous    index    next ->

Lecture 27b, Partial Differential Equations Initial Conditions 


Some partial differential equations are difficult to solve symbolically
and some are difficult to solve numerically.

This lecture covers the numerical solution of simple partial
differential equations where the initial conditions values are known.

See  simple definitions .

We know from lectures on derivatives:

Given a function U(x,y) and points x0, x1, x2, y0, x1=x0+h, x2=x1+h
dU(x0,y0)/dx = Ux(x0,y0) = (-3*U(x0,y0) +4*U(x1,y0) -1*U(x2,y0) )/ 2h
               Ux(x1,y0) = (-1*U(x0,y0)             +1*U(x2,y0) )/ 2h
               Ux(x2,y0) = ( 1*U(x0,y0) -4*U(x1,y0) +3*U(x2,y0) )/ 2h
adding         ------------------------------------------------------
               Ux(x0,y0)+U(x1,y0)+Ux(x2,y0) = (-3*U(x0,y0) +3*U(x2,y0)) /2h
divide by 3
rearrange      U(x2,y0) = U(x0,y0) + 2*h*(Ux(x0,y0)+U(x1,y0)+Ux(x2,y0))/3

Thus we have a way to compute a new value of U, knowing a previous value
and derivatives. Changing the notation to go from point xa to xb=xa+hx :
          U(xb,y0) = U(xa,y0) + hx*(Ux(xa,y0)+Ux(xa+hx/2,y0)+Ux(xa+hx,y0))/3 

Sample test case for above
 source code  pde_i1.java
 source code  pde_i1_java.out

We are told there is an unknown function U(x,y) that satisfies
the a differential equation:
   Given the value of U(x0,y0)         only one point
   Given a computable function Ux(x,y)
   Given a computable function Uy(x,y)
We can compute U(x,y) at an array of points x0 to xmax, y0 to ymax
with step size hx and hy.

Sample test case for above
 source code  pde_i2.java
 source code  pde_i2_java.out

PDE with computable Ux(x,y) and U(y(x,y) and known U(x0,y0)


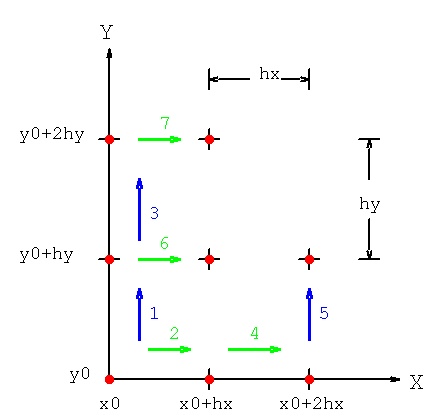1 compute U(x0,y0+hy) = U(x0,y0) + hy*Uy(x0,y0) or higher order method
2 compute U(x0+hx,y0) = U(x0,y0) + hx*Ux(x0,y0)
3 compute U(x0,y0+2*hy) = U(x0,y0+hy) + hy*Uy(x0,y0+hy) 
4 compute U(x0+2*hx,y0) = U(x0+hx,y0) + hx*Ux(x0+hx,y0)
5 compute U(x0+2*hx,y0+hy) = U(x0+2*hx,y0) + hy*Uy(x0+2*hx,y0)
6 compute U(x0+hx,y0+hy) = U(x0,y0+hy) + hx*Ux(x0,y0+hy)
7 compute U(x0+hx,y0+2*hy) = U(x0,y0+2*hy) + hx*Ux(x0,y0+2*hy)

A higher order method can use hx/2 and Ux(x0+hx/2,y0+hy/2)  etc.
There are two ways to compute U(x0+hy,y0+hy) and many options beyond that.


more examples using MATLAB built in ODE solvers

stiff.m MATLAB source code

% stiff.m  using  ode15s
function stiff()
[t,y]=ode15s(@vdp1000, [0 3000], [2 0]);
  plot(t,y(:,1),'-o')

  function dydt = vdp1000(t, y)
    dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];
  end % vdp1000
end % stiff



stiff1.m MATLAB source code

% stiff1.m  using  ode23
% y1' = y2    y2' = (1-y1^2)*y2-y1
function stiff1()
  [t,y]=ode23(@vdp, [0 20], [2; 0]);
  plot(t,y(:,1),'-o',t,y(:,2),'-o')
  title('Solution of van der Pol Equation (\mu = 1) with ODE23');
  xlabel('Time t');
  ylabel('Solution y');
  legend('y_1','y_2')

  function dydt = vdp(t, y)
    dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];
  end % vdp
end % stiff1



ode21.m MATLAB source code

% ode21.m   second oder ode with initial conditions
function ode21
  % SOLVE  d^2x/d^2t + 5*dx/dt - 4 x = sin(10 t)
  % initial conditions: x(0) = 0, x'(0)=0
  t=0:0.001:3;   % time scale

  initial_x    = 0;
  initial_dxdt = 0;
  [t,x]=ode45( @rhs, t, [initial_x initial_dxdt] );

  plot(t,x(:,1),t,x(:,2));
  title('solve d^2x/d^2t + 5*dx/dt - 4 x = sin(10 t)');
  xlabel('t');
  ylabel('x');
  legend('dx_1','dx_2');

  function dxdt=rhs(t,x)
    dxdt_1 = x(2);
    dxdt_2 = -5*x(2) + 4*x(1) + sin(10*t);
    dxdt=[dxdt_1; dxdt_2];
  end % rhs
end % ode21


ode_1.m MATLAB source code

% ode_1.m  using ode45 with setup
function ode_1
  options = odeset('RelTol', 1e-4, 'AbsTol', [1e-4 1e-4 1e-5]);
  [T,Y] = ode45(@ridgid, [0 12], [0 1 1], options);
  plot(T, Y(:,1), '-', T, Y(:,2), '-.', T, Y(:,3), '.')
  title('second order solution with ode45');
  xlabel('Time T');
  ylabel('Solution Y');
  legend('dy_1','dy_2','dy_3');

  function dy=ridgid(t, y)
   dy = zeros(3, 1);  % force a column vector
   dy(1) = y(2) * y(3);
   dy(2) = -y(1) * y(3);
   dy(3) = -0.51 * y(1) * y(2);
  end % ridgid
end % ode_1




    <- previous    index    next ->

Other links

Go to top