<- previous index next ->
Numerical differentiation can be applied to all orders in
all coordinate systems.
It gets more complicated, yet a reasonable extension of Cartesian
coordinate systems. These are all partial derivatives.
This page will develop Spherical derivatives up to fourth order
from corresponding Cartesian derivatives.
∇f(x,y,z,t) = ∂f/∂x + ∂f/∂y + ∂f/∂z + ∂f/∂t
∇2f(x,y,z,t) = ∂2f/∂x2 + ∂2f/∂y2 + ∂2f/∂z2 + ∂2f/∂t2
∇3f(x,y,z,t) = ∂3f/∂x3 + ∂3f/∂y3 + ∂3f/∂z3 + ∂3f/∂t3
∇4f(x,y,z,t) = ∂4f/∂x4 + ∂4f/∂y4 + ∂4f/∂z4 + ∂4f/∂t4
Spherical coordinates
Choice of convention:
Theta Θ below is angle from Z axis.
Phi Φ below is angle from X axis in X Y plane
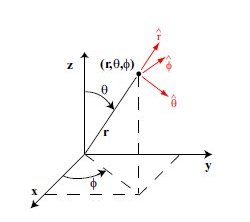 x = r * sin(Θ) * cos(Φ) r = sqrt(x^2 + y^2 + z^2) 0 < r
y = r * sin(Θ) * sin(Φ) Φ = atan2(y,x) 0 ≤ Φ < 2Π
Φ = acos(x/sqrt(x^2+y^2))
Φ = asin(y/sqrt(x^2+y^2))
z = r * cos(Θ) Θ = atan2(sqrt(x^2+y^2),z) 0 < Θ < Π
θ = acos(z/sqrt(x^2+y^2+z^2))
θ = asin(sqrt(x^2+y^2)/sqrt(x^2+y^2+z^2))
cos(Θ) = z/r = z/sqrt(x^2 + y^2 + z^2)
sin(Θ) = sqrt(x^2 + y^2)/r
cos(Φ) = x/sqrt(x^2 + y^2)
sin(Φ) = y/sqrt(x^2 + y^2)
Gradient ∇f a vector
^ ^ ^
∇f(r,Θ,Φ) = r ∂f/∂r + Θ 1/r ∂f/∂Θ + Φ 1/r sin(Φ) ∂f/∂φ
Laplacian ∇2f a scalar, divergence ∇˙f
∇2f(r,Θ,Φ) = 1/r2 ∂/∂r(r2*∂f/∂r) + 1/(r2 sin(Θ)) ∂f/∂Θ(sin(Θ) ∂f/∂Θ) + 1/(r2 sin(Θ)2) ∂2f/∂2Φ
= 2/r ∂f/∂r + ∂2f/∂r2 + cos(Θ)/(r2 sin(Θ)2 ∂f/∂Θ + 1/(r2 ∂2f/∂Θ2 + 1/(r2 sin(Θ)2) ∂2f/∂Φ2
∇✗f curl a vector
∇✗f = {1/(r sin(Θ))(∂/∂Θ(fφ sin(Θ))- ∂fθ/∂Φ) ,
1/r (1/sin(Θ) ∂fr/∂Φ - ∂/∂r(r fθ) ,
1/r (∂/∂r(r fφ - ∂fr/∂Θ) }
x = r * sin(Θ) * cos(Φ) r = sqrt(x^2 + y^2 + z^2) 0 < r
y = r * sin(Θ) * sin(Φ) Φ = atan2(y,x) 0 ≤ Φ < 2Π
Φ = acos(x/sqrt(x^2+y^2))
Φ = asin(y/sqrt(x^2+y^2))
z = r * cos(Θ) Θ = atan2(sqrt(x^2+y^2),z) 0 < Θ < Π
θ = acos(z/sqrt(x^2+y^2+z^2))
θ = asin(sqrt(x^2+y^2)/sqrt(x^2+y^2+z^2))
cos(Θ) = z/r = z/sqrt(x^2 + y^2 + z^2)
sin(Θ) = sqrt(x^2 + y^2)/r
cos(Φ) = x/sqrt(x^2 + y^2)
sin(Φ) = y/sqrt(x^2 + y^2)
Gradient ∇f a vector
^ ^ ^
∇f(r,Θ,Φ) = r ∂f/∂r + Θ 1/r ∂f/∂Θ + Φ 1/r sin(Φ) ∂f/∂φ
Laplacian ∇2f a scalar, divergence ∇˙f
∇2f(r,Θ,Φ) = 1/r2 ∂/∂r(r2*∂f/∂r) + 1/(r2 sin(Θ)) ∂f/∂Θ(sin(Θ) ∂f/∂Θ) + 1/(r2 sin(Θ)2) ∂2f/∂2Φ
= 2/r ∂f/∂r + ∂2f/∂r2 + cos(Θ)/(r2 sin(Θ)2 ∂f/∂Θ + 1/(r2 ∂2f/∂Θ2 + 1/(r2 sin(Θ)2) ∂2f/∂Φ2
∇✗f curl a vector
∇✗f = {1/(r sin(Θ))(∂/∂Θ(fφ sin(Θ))- ∂fθ/∂Φ) ,
1/r (1/sin(Θ) ∂fr/∂Φ - ∂/∂r(r fθ) ,
1/r (∂/∂r(r fφ - ∂fr/∂Θ) }
testing equations for correct numerical output
check_thetaphi_deriv.c
check_thetaphi_deriv_c.out
Then, to compute ∇4 you may use Maple
spherical4.mws
spherical4_mws.out
<- previous index next ->
 x = r * sin(Θ) * cos(Φ) r = sqrt(x^2 + y^2 + z^2) 0 < r
y = r * sin(Θ) * sin(Φ) Φ = atan2(y,x) 0 ≤ Φ < 2Π
Φ = acos(x/sqrt(x^2+y^2))
Φ = asin(y/sqrt(x^2+y^2))
z = r * cos(Θ) Θ = atan2(sqrt(x^2+y^2),z) 0 < Θ < Π
θ = acos(z/sqrt(x^2+y^2+z^2))
θ = asin(sqrt(x^2+y^2)/sqrt(x^2+y^2+z^2))
cos(Θ) = z/r = z/sqrt(x^2 + y^2 + z^2)
sin(Θ) = sqrt(x^2 + y^2)/r
cos(Φ) = x/sqrt(x^2 + y^2)
sin(Φ) = y/sqrt(x^2 + y^2)
Gradient ∇f a vector
^ ^ ^
∇f(r,Θ,Φ) = r ∂f/∂r + Θ 1/r ∂f/∂Θ + Φ 1/r sin(Φ) ∂f/∂φ
Laplacian ∇2f a scalar, divergence ∇˙f
∇2f(r,Θ,Φ) = 1/r2 ∂/∂r(r2*∂f/∂r) + 1/(r2 sin(Θ)) ∂f/∂Θ(sin(Θ) ∂f/∂Θ) + 1/(r2 sin(Θ)2) ∂2f/∂2Φ
= 2/r ∂f/∂r + ∂2f/∂r2 + cos(Θ)/(r2 sin(Θ)2 ∂f/∂Θ + 1/(r2 ∂2f/∂Θ2 + 1/(r2 sin(Θ)2) ∂2f/∂Φ2
∇✗f curl a vector
∇✗f = {1/(r sin(Θ))(∂/∂Θ(fφ sin(Θ))- ∂fθ/∂Φ) ,
1/r (1/sin(Θ) ∂fr/∂Φ - ∂/∂r(r fθ) ,
1/r (∂/∂r(r fφ - ∂fr/∂Θ) }
x = r * sin(Θ) * cos(Φ) r = sqrt(x^2 + y^2 + z^2) 0 < r
y = r * sin(Θ) * sin(Φ) Φ = atan2(y,x) 0 ≤ Φ < 2Π
Φ = acos(x/sqrt(x^2+y^2))
Φ = asin(y/sqrt(x^2+y^2))
z = r * cos(Θ) Θ = atan2(sqrt(x^2+y^2),z) 0 < Θ < Π
θ = acos(z/sqrt(x^2+y^2+z^2))
θ = asin(sqrt(x^2+y^2)/sqrt(x^2+y^2+z^2))
cos(Θ) = z/r = z/sqrt(x^2 + y^2 + z^2)
sin(Θ) = sqrt(x^2 + y^2)/r
cos(Φ) = x/sqrt(x^2 + y^2)
sin(Φ) = y/sqrt(x^2 + y^2)
Gradient ∇f a vector
^ ^ ^
∇f(r,Θ,Φ) = r ∂f/∂r + Θ 1/r ∂f/∂Θ + Φ 1/r sin(Φ) ∂f/∂φ
Laplacian ∇2f a scalar, divergence ∇˙f
∇2f(r,Θ,Φ) = 1/r2 ∂/∂r(r2*∂f/∂r) + 1/(r2 sin(Θ)) ∂f/∂Θ(sin(Θ) ∂f/∂Θ) + 1/(r2 sin(Θ)2) ∂2f/∂2Φ
= 2/r ∂f/∂r + ∂2f/∂r2 + cos(Θ)/(r2 sin(Θ)2 ∂f/∂Θ + 1/(r2 ∂2f/∂Θ2 + 1/(r2 sin(Θ)2) ∂2f/∂Φ2
∇✗f curl a vector
∇✗f = {1/(r sin(Θ))(∂/∂Θ(fφ sin(Θ))- ∂fθ/∂Φ) ,
1/r (1/sin(Θ) ∂fr/∂Φ - ∂/∂r(r fθ) ,
1/r (∂/∂r(r fφ - ∂fr/∂Θ) }