Note that this file is plain text and .gif files. The plain text spells out Greek letters because old browsers did not display them.
These are not intended to be complete lecture notes. Complicated figures or tables or formulas are included here in case they were not clear or not copied correctly in class. Information from the language definitions, automata definitions, computability definitions and class definitions is not duplicated here. Lecture numbers correspond to the syllabus numbering.
This course covers some of the fundamental beginnings and foundations of computers and software. From automata to Turing Machines and formal languages to our programming languages, an interesting progression. A fast summary of what will be covered in this course (part 1) For reference, skim through the automata definitions and language definitions and grammar definitions to get the terms that will be used in this course. Don't panic, this will be easy once it is explained. Syllabus provides topics, homework and exams. HW1 is assigned Oh! "Formal Language" vs "Natural Language" Boy hit ball. word word word punctuation tokens noun verb noun period parsed subject predicate object sentence semantic "Language" all legal sentences In this class language will be a set of strings from a given alphabet. All math operations on sets apply, examples: union, concatenation, intersection, cross product, etc. We will cover grammars that define languages. We will define machines called automata that accept languages.
A fast summary of what will be covered in this course (part 2) For reference, read through the computability definitions and complexity class definitions
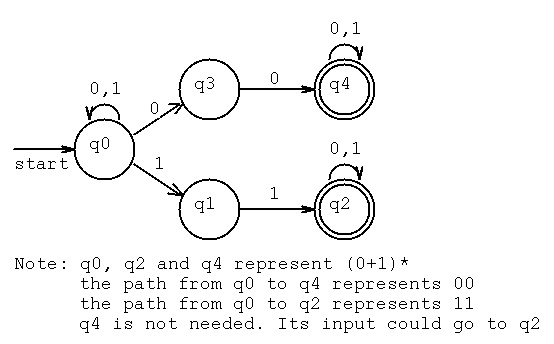
Example of a Deterministic Finite Automata, DFA
Machine Definition M = (Q, Sigma, delta, q0, F)
Q = { q0, q1, q2, q3, q4 } the set of states (finite)
Sigma = { 0, 1 } the input string alphabet (finite)
delta the state transition table - below
q0 = q0 the starting state
F = { q2, q4 } the set of final states (accepting
when in this state and no more input)
inputs
delta | 0 | 1 |
---------+---------+---------+
q0 | q3 | q1 |
q1 | q1 | q2 |
states q2 | q2 | q2 |
q3 | q4 | q3 |
q4 | q4 | q4 |
^ ^ ^
| | |
| +---------+-- every transition must have a state
+-- every state must be listed

An exactly equivalent diagram description for the machine M.
Each circle is a unique state. The machine is in exactly one state
and stays in that state until an input arrives. Connection lines
with arrows represent a state transition from the present state
to the next state for the input symbol(s) by the line.
L(M) is the notation for a Formal Language defined by a machine M.
Some of the shortest strings in L(M) = { 00, 11, 000, 001, 010, 101, 110,
111, 0000, 0001, 0010, 0011, 0100, 0101, 0110, 1001, ... }
The regular expression for this state diagram is
r = (0(1*)0(0+1)*)+(1(0*)1(0+1)*) using + for or, * for kleene star
1|--|
| V
//--\\
|| q3 || is a DFA with regular expression r = (1*)
\\--// zero or more sequence of 1 (infinite language)
0|--|
1| v
//--\\ is a DFA with regular expression r = (0+1)*
|| q4 || zero or more sequence of 0 or 1 in any order 00 01 10 11 etc
\\--// at end because final state (infinite language)
In words, L is the set of strings over { 0, 1} that contain at least
two 0's starting with 0, or that contain at least two 1's starting with 1.
Every input sequence goes through a sequence of states, for example
00 q0 q3 q4
11 q0 q1 q2
000 q0 q3 q4 q4
001 q0 q3 q4 q4
010 q0 q3 q3 q4
011 q0 q3 q3 q3
0110 q0 q3 q3 q3 q4
Rather abstract, there are tens of millions of DFA being used today.
practical example DFA
More information on DFA
More files, examples:
example data input file reg.dfa
example output from dfa.cpp, reg.out
under development dfa.java dfa.py
example output from dfa.java, reg_def_java.out
example output from dfa.py, labc_def_py.out
/--\ a /--\ b /--\ c //--\\
labc.dfa is -->| q0 |--->| q1 |--->| q2 |--->|| q3 || using just characters
\--/ \--/ \--/ \\--//
example data input file labc.dfa
example output from dfa.py, labc_def_py.out
For future homework, you can download programs and sample data from
cp /afs/umbc.edu/users/s/q/squire/pub/download/reg.dfa .
and other files
Definition of a Regular Expression
------------------
A regular expression may be the null string,
r = epsilon
A regular expression may be an element of the input alphabet, a in sigma,
r = a
A regular expression may be the union of two regular expressions,
r = r1 + r2 the plus sign is "or"
A regular expression may be the concatenation (no symbol) of two
regular expressions,
r = r1 r2
A regular expression may be the Kleene closure (star) of a
regular expression, may be null string or any number of concatenations of r1
r = r1* (the asterisk should be a superscript,
but this is plain text)
A regular expression may be a regular expression in parenthesis
r = (r1)
Nothing is a regular expression unless it is constructed with only the
rules given above.
The language represented or generated by a regular expression is a
Regular Language, denoted L(r).
The regular expression for the machine M above is
r = (1(0*)1(0+1)*)+(0(1*)0(0+1)*)
\ \ any number of zeros and ones
\ any number of zero
Later we will give an algorithm for generating a regular expression from
a machine definition. For simple DFA's, start with each accepting
state and work back to the start state writing the regular expression.
The union of these regular expressions is the regular expression for
the machine.
For every DFA there is a regular language and for every regular language
there is a regular expression. Thus a DFA can be converted to a
regular expression and a regular expression can be converted to a DFA.
Some examples, a regular language with only 0 in alphabet,
with strings of length 2*n+1 for n>0. Thus infinite language yet
DFA must have a finite number of states and finite number of
transitions to accept {000, 00000, 0000000, ...) 2*n+1 = 3,5,7,...
The DFA state diagram is
/--\ 0 /--\ 0 /--\ 0 //--\\ 0
| q0 |-->| q0 |-->| q0 |--->|| q4 ||--+
\--/ \--/ \--/ \\--// |
^ |
+---------------+
Check it out: 000 accepted, then 00000 two more 0 then accepted, ...
Now, an example of the complement of a regular expression is
a regular expression. First a DFA that accepts any string with 00
then a DFA that does not accept any string with 00, the complement.
|--|<-------+ |--------+ r = ((1)*0)*0(0+1)*
V |1 |1 V |
/--\ 0 /--\ 0 //--\\ |1 any 00
-| q0 |-->| q1 |-->|| q2 ||--+ (1)* can be empty string
\--/ \--/ \\--// |0
^ |
|--------+
+-----------------+
| /--\-+ 1 /--\ 0
| +-->| q1 |--->| q2 |----+ r = ((1*)+0(1*))*
V 0 | \--/ 0 \--/---+ |
//--\\---+ ^ ^ 1| | no 00
-|| q0 || | +---+ |
\\--//---+ +--------+
^ 1 | never leaves, never accepted
+----+
The general way to create a complement of a regular expression is to
create a new regular expression that has all of the first regular
expression go to phi and all other strings go to a final state.
Both regular expressions must have the same alphabet.

Given a DFA and one or more strings, determine if the string(s) are accepted by the DFA. This may be error prone and time consuming to do by hand. Fortunately, there is a program available to do this for you. On linux.gl.umbc.edu do the following: ln -s /afs/umbc.edu/users/s/q/squire/pub/dfa dfa cp /afs/umbc.edu/users/s/q/squire/pub/download/ab_b.dfa . dfa < ab_b.dfa # or dfa < ab_b.dfa > ab_a.out Full information is available at Simulators The source code for the family of simulators is available. HW2 is assigned last update 3/9/2021
Here, we start with the state diagram:
From this we see the states Q = { Off, Starting forward, Running forward, Starting reverse, Running reverse } The alphabet (inputs) Sigma = { off request, forward request, reverse request, time-out } The initial state would be Off. The final state would be Off. The state transition table, Delta, is obvious yet very wordy. Note: that upon entering a state, additional actions may be specified. Inputs could be from buttons, yet could come from a computer.
Important! nondeterministic has nothing to do with random,
nondeterministic implies parallelism.
The difference between a DFA and a NFA is that the state transition
table, delta, for a DFA has exactly one target state but for a NFA has
a set, possibly empty (phi), of target states.
A NFA state diagram may have more than one line to get
to some state.
Example of a NFA, Nondeterministic Finite Automata given
by a) Machine Definition M = (Q, sigma, delta, q0, F)
b) Equivalent regular expression
c) Equivalent state transition diagram
and example tree of states for input string 0100011
and an equivalent DFA, Deterministic Finite Automata for the
first 3 states.
a) Machine Definition M = (Q, sigma, delta, q0, F)
Q = { q0, q1, q2, q3, q4 } the set of states
sigma = { 0, 1 } the input string alphabet
delta the state transition table
q0 = q0 the starting state
F = { q2, q4 } the set of final states (accepting when in
this state and no more input)
inputs
delta | 0 | 1 |
---------+---------+---------+
q0 | {q0,q3} | {q0,q1} |
q1 | phi | {q2} |
states q2 | {q2} | {q2} |
q3 | {q4} | phi |
q4 | {q4} | {q4} |
^ ^ ^
| | |
| +---------+-- a set of states, phi means empty set
+-- every state must be listed
b) The equivalent regular expression is (0+1)*(00+11)(0+1)*
This NFA represents the language L = all strings over {0,1} that
have at least two consecutive 0's or 1's.
c) Equivalent NFA state transition diagram.
Note that state q3 does not go anywhere for an input of 1.
We use the terminology that the path "dies" if in q3 getting an input 1.
The tree of states this NFA is in for the input 0100011
input
q0
/ \ 0
q3 q0
dies / \ 1
q1 q0
dies / \ 0
q3 q0
/ / \ 0
q4 q3 q0
/ / / \ 0
q4 q4 q3 q0
/ / dies / \ 1
q4 q4 q1 q0
/ / / / \ 1
q4 q4 q2 q1 q0
^ ^ ^
| | |
accepting paths in NFA tree
Construct a DFA equivalent to the NFA above using just the first
three rows of delta (for brevity, consider q3 and q4 do not exists).
The DFA machine is M' = (Q', sigma, delta', q0', F')
The set of states is
Q' = 2**Q, the power set of Q = { phi, {q0}, {q1}, {q2}, {q0,q1}, {q0,q2},
{q1,q2}, {q0,q1,q2} }
Note the big expansion: If a set has n items, the power set has 2^n items.
Note: read the eight elements of the set Q' as names of states of M'
OK to use [ ] in place of { } if you prefer.
sigma is the same sigma = { 0, 1}
The state transition table delta' is given below
The starting state is set containing only q0 q0' = {q0}
The set of final states is a set of sets that contain q2
F' = { {q2}, {q0,q2}, {q1,q2}, {q0,q1,q2} }
Algorithm for building delta' from delta:
The delta' is constructed directly from delta.
Using the notation f'({q0},0) = f(q0,0) to mean:
in delta' in state {q0} with input 0 goes to the state
shown in delta with input 0. Take the union of all such states.
Further notation, phi is the empty set so phi union the set A is
just the set A.
Some samples: f'({q0,q1},0) = f(q0,0) union f(q1,0) = {q0}
f'({q0,q1},1) = f(q0,1) union f(q1,1) = {q0,q1,q2}
f'({q0,q2},0) = f(q0,0) union f(q2,0) = {q0,q2}
f'({q0,q2},1) = f(q0,1) union f(q2,1) = {q0,q1,q2}
sigma
delta | 0 | 1 | simplified for this construction
---------+---------+---------+
q0 | {q0} | {q0,q1} |
states q1 | phi | {q2} |
q2 | {q2} | {q2} |
sigma
delta' | 0 | 1 |
----------+-------------+-------------+
phi | phi | phi | never reached
{q0} | {q0} | {q0,q1} |
states {q1} | phi | {q2} | never reached
Q' {q2} | {q2} | {q2} | never reached
{q0,q1} | {q0} | {q0,q1,q2} |
{q0,q2} | {q0,q2} | {q0,q1,q2} |
{q1,q2} | {q2} | {q2} | never reached
{q0,q1,q2} | {q0,q2} | {q0,q1,q2} |
Note: Some of the states in the DFA may be unreachable yet
must be specified. Later we will use Myhill minimization.

DFA (not minimized) equivalent to lower branch of NFA above.
The sequence of states is unique for a DFA, so for the same input as
above 0100011 the sequence of states is
{q0} 0 {q0} 1 {q0,q1} 0 {q0} 0 {q0} 0 {q0} 1 {q0,q1}
1 {q0,q1,q2}
This sequence does not have any states involving q3 or q4 because just
a part of the above NFA was converted to a DFA. This DFA does not
accept the string 00 whereas the NFA above does accept 00.
Given a NFA and one or more strings, determine if the string(s)
are accepted by the NFA. This may be error prone and time
consuming to do by hand. Fortunately, there is a program
available to do this for you.
On linux.gl.umbc.edu do the following:
ln -s /afs/umbc.edu/users/s/q/squire/pub/nfa nfa
cp /afs/umbc.edu/users/s/q/squire/pub/download/fig2_7.nfa .
nfa < fig2_7.nfa # or nfa < fig2_7.nfa > fig2_7.out
NFA coded for simulation
You can code a Machine Definition into a data file for simulation
Q = { q0, q1, q2, q3, q4 }
sigma = { 0, 1 } // fig2_7.nfa
delta
q0 = q0 start q0
F = { q2, q4 } final q2
final q4
sigma
delta | 0 | 1 | q0 0 q0
---------+---------+---------+ q0 0 q3
q0 | {q0,q3} | {q0,q1} | q0 1 q0
q1 | phi | {q2} | q0 1 q1
states q2 | {q2} | {q2} | q1 1 q2
q3 | {q4} | phi | q2 0 q2
q4 | {q4} | {q4} | q2 1 q2
q3 0 q4
q4 0 q4
q4 1 q4
enddef
tape 10101010 // reject
tape 10110101 // accept
tape 10100101 // accept
tape 01010101 // reject
Full information is available at Simulators
The source code for the family of simulators is available.
Definition and example of a NFA with epsilon transitions.
Remember, epsilon is the zero length string, so it can be any where
in the input string, front, back, between any symbols.
There is a conversion algorithm from a NFA with epsilon transitions to
a NFA without epsilon transitions.
Consider the NFA-epsilon move machine M = { Q, sigma, delta, q0, F}
Q = { q0, q1, q2 }
sigma = { a, b, c } and epsilon moves
q0 = q0
F = { q2 }
sigma plus epsilon
delta | a | b | c |epsilon
------+------+------+------+-------
q0 | {q0} | phi | phi | {q1}
------+------+------+------+-------
q1 | phi | {q1} | phi | {q2}
------+------+------+------+-------
q2 | phi | phi | {q2} | {q2}
------+------+------+------+-------

The language accepted by the above NFA with epsilon moves is
the set of strings over {a,b,c} including the null string and
all strings with any number of a's followed by any number of b's
followed by any number of c's. ("any number" includes zero)
Now convert the NFA with epsilon moves to a NFA
M = ( Q', sigma, delta', q0', F')
First determine the states of the new machine, Q' = the epsilon closure
of the states in the NFA with epsilon moves. There will be the same
number of states but the names can be constructed by writing the state
name as the set of states in the epsilon closure. The epsilon closure
is the initial state and all states that can be reached directly
by one or more epsilon moves.
Thus q0 in the NFA-epsilon becomes {q0,q1,q2} because the machine can
move from q0 to q1 by an epsilon move, then check q1 and find that
it can move from q1 to q2 by an epsilon move.
q1 in the NFA-epsilon becomes {q1,q2} because the machine can move from
q1 to q2 by an epsilon move.
q2 in the NFA-epsilon becomes {q2} just to keep the notation the same. q2
can go nowhere except q2, that is what phi means, on an epsilon move.
We do not show the epsilon transition of a state to itself here, but,
beware, we will take into account the state to itself epsilon transition
when converting NFA's to regular expressions.
The initial state of our new machine is {q0,q1,q2} the epsilon closure
of q0
The final state(s) of our new machine is the new state(s) that contain
a state symbol that was a final state in the original machine.
The new machine accepts the same language as the old machine,
thus same sigma.
So far we have for out new NFA
Q' = { {q0,q1,q2}, {q1,q2}, {q2} } or renamed { qx, qy, qz }
sigma = { a, b, c }
F' = { {q0,q1,q2}, {q1,q2}, {q2} } or renamed { qx, qy, qz }
q0 = {q0,q1,q2} or renamed qx
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | | |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
Now we fill in the transitions. Remember that a NFA has transition
entries that are sets. Further, the names in the transition entry
sets must be only the state names from Q'.
Very carefully consider each old machine transitions in the first row.
You can ignore any "phi" entries and ignore the "epsilon" column.
In the old machine delta(q0,a)=q0 thus in the new machine
delta'({q0,q1,q2},a)={q0,q1,q2} this is just because the new machine
accepts the same language as the old machine and must at least have the
the same transitions for the new state names.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
No more entries go under input a in the first row because
old delta(q1,a)=phi, delta(q2,a)=phi
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | |
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | |
------------+--------------+--------------+--------------
qz or {q2} | phi | |
------------+--------------+--------------+--------------
Now consider the input b in the first row, delta(q0,b)=phi,
delta(q1,b)={q2} and delta(q2,b)=phi. The reason we considered
q0, q1 and q2 in the old machine was because out new state
has symbols q0, q1 and q2 in the new state name from the
epsilon closure. Since q1 is in {q0,q1,q2} and
delta(q1,b)=q1 then delta'({q0,q1,q2},b)={q1,q2}. WHY {q1,q2} ?,
because {q1,q2} is the new machines name for the old machines
name q1. Just compare the zeroth column of delta to delta'. So we have
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} |
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | |
------------+--------------+--------------+--------------
qz or {q2} | phi | |
------------+--------------+--------------+--------------
Now, because our new qx state has a symbol q2 in its name and
delta(q2,c)=q2 is in the old machine, the new name for the old q2,
which is qz or {q2} is put into the input c transition in row 1.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} | {{q2}} or qz
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | |
------------+--------------+--------------+--------------
qz or {q2} | phi | |
------------+--------------+--------------+--------------
Now, tediously, move on to row two ..., column b ...
You are considering all transitions in the old machine, delta,
for all old machine state symbols in the name of the new machines states.
Fine the old machine state that results from an input and translate
the old machine state to the corresponding new machine state name and
put the new machine state name in the set in delta'. Below are the
"long new state names" and the renamed state names in delta'.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} | {{q2}} or {qz}
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | {{q1,q2}} | {{q2}} or {qz}
------------+--------------+--------------+--------------
qz or {q2} | phi | phi | {{q2}} or {qz}
------------+--------------+--------------+--------------
inputs
delta' | a | b | c <-- input alphabet sigma
---+------+------+-----
/ qx | {qx} | {qy} | {qz}
/ ---+------+------+-----
Q' qy | phi | {qy} | {qz}
\ ---+------+------+-----
\ qz | phi | phi | {qz}
---+------+------+-----
The figure above labeled NFA shows this state transition table.
It seems rather trivial to add the column for epsilon transitions,
but we will make good use of this in converting regular expressions
to machines. regular-expression -> NFA-epsilon -> NFA -> DFA.
HW3 is assigned
Given a regular expression, r , there is an associated regular language L(r).
Since there is a finite automata for every regular language,
there is a machine, M, for every regular expression such that L(M) = L(r).
The constructive proof provides an algorithm for constructing a machine, M,
from a regular expression r. The six constructions below correspond to
the cases:
1) The entire regular expression is the null string, i.e. L={epsilon}
(Any regular expression that includes epsilon will have the
starting state as a final state.)
r = epsilon
2) The entire regular expression is empty, i.e. L=phi r = phi
3) An element of the input alphabet, sigma, is in the regular expression
r = a where a is an element of sigma.
4) Two regular expressions are joined by the union operator, +
r1 + r2
5) Two regular expressions are joined by concatenation (no symbol)
r1 r2
6) A regular expression has the Kleene closure (star) applied to it
r*
The construction proceeds by using 1) or 2) if either applies.
The construction first converts all symbols in the regular expression
using construction 3).
Then working from inside outward, left to right at the same scope,
apply the one construction that applies from 4) 5) or 6).
 Example: Convert (00 + 1)* 1 (0 +1) to a NFA-epsilon machine.
Optimization hint: We use a simple form of epsilon-closure to combine
any state that has only an epsilon transition to another state, into
one state.
chose first 0 to get
Example: Convert (00 + 1)* 1 (0 +1) to a NFA-epsilon machine.
Optimization hint: We use a simple form of epsilon-closure to combine
any state that has only an epsilon transition to another state, into
one state.
chose first 0 to get
 chose next 0, and concatenate
chose next 0, and concatenate
 use epsilon-closure to combine states
use epsilon-closure to combine states
 Chose 1, then added union
Chose 1, then added union
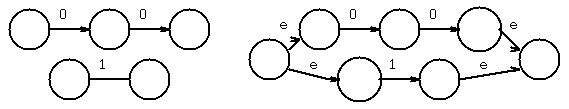 Apply Kleene star
Apply Kleene star
 Chose 1, concatenate, combine states
Chose 1, concatenate, combine states
 Concatenate (0+1), combine one state
Concatenate (0+1), combine one state
 The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4 in 1st Ed. or section 4.4 in 2nd Ed.
This will provide a DFA that has the minimum number of states.
Within a renaming of the states and reordering of the delta, state
transition table, all minimum machines of a DFA are identical.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
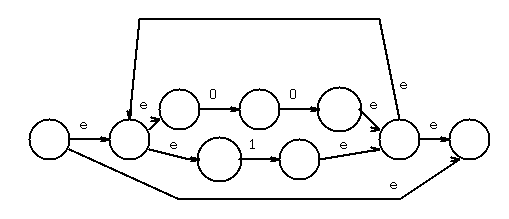
Example: r = (0+1)* (00+11) (0+1)*
Solution: find the primary operator(s) that are concatenation or union.
In this case, the two outermost are concatenation, giving, crudely:
//---------------\ /----------------\\ /-----------------\
-->|| <> M((0+1)*) <> |->| <> M((00+11)) <> ||->| <> M((0+1)*) <<>> |
\\---------------/ \----------------// \-----------------/
There is exactly one start "-->" and exactly one final state "<<>>"
The unlabeled arrows should be labeled with epsilon.
Now recursively decompose each internal regular expression.
The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4 in 1st Ed. or section 4.4 in 2nd Ed.
This will provide a DFA that has the minimum number of states.
Within a renaming of the states and reordering of the delta, state
transition table, all minimum machines of a DFA are identical.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
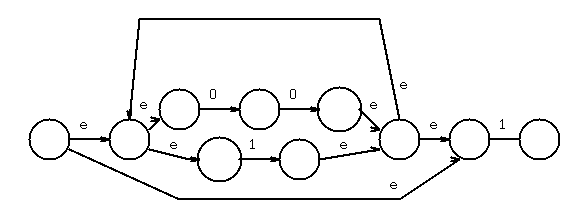
Example: r = (0+1)* (00+11) (0+1)*
Solution: find the primary operator(s) that are concatenation or union.
In this case, the two outermost are concatenation, giving, crudely:
//---------------\ /----------------\\ /-----------------\
-->|| <> M((0+1)*) <> |->| <> M((00+11)) <> ||->| <> M((0+1)*) <<>> |
\\---------------/ \----------------// \-----------------/
There is exactly one start "-->" and exactly one final state "<<>>"
The unlabeled arrows should be labeled with epsilon.
Now recursively decompose each internal regular expression.
Conversion algorithm from a NFA to a regular expression.
Start with the transition table for the NFA with the following
state naming conventions:
the first state is 1 or q1 or s1 which is the starting state.
states are numbered consecutively, 1, 2, 3, ... n
The transition table is a typical NFA where the table entries
are sets of states and phi the empty set is allowed.
The set F of final states must be known.
We call the variable r a regular expression.
It can be: epsilon, an element of the input sigma, r*, r1+r2, or r1 r2
We use r being the regular expression to go from state qi to qj
ij
We need multiple steps from state qi to qj and use a superscript
to show the number of steps
1 2 k k-1
r r r r are just names of different regular expressions
12 34 1k ij
2
We are going to build a table with n rows and n+1 columns labeled
| k=0 | k=1 | k=2 | ... | k=n
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | | n
r | r | r | r | ... | r Only build column n
11 | 11 | 11 | 11 | | 11 for q1 to final state
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | | n The final regular expression
r | r | r | r | ... | r is then the union, +, of
12 | 12 | 12 | 12 | | 12 the column n
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | | n
r | r | r | r | ... | r
13 | 13 | 13 | 13 | | 13
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
21 | 21 | 21 | 21 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
22 | 22 | 22 | 22 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
23 | 23 | 23 | 23 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
31 | 31 | 31 | 31 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
32 | 32 | 32 | 32 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
33 | 33 | 33 | 33 | |
^ 2
|- Note n rows, all pairs of numbers from 1 to n
Now, build the table entries for the k=0 column:
/
0 / +{ x | delta(q ,x) = q } i /= j
r = / i j
ij \
\ +{ x | delta(q ,x) = q } + epsilon i = j
\ i j
where delta is the transition table function,
x is some symbol from sigma
the q's are states
0
r could be phi, epsilon, a, 0+1, or a+b+d+epsilon
ij
notice there are no Kleene Star or concatenation in this column
Next, build the k=1 column:
1 0 0 * 0 0
r = r ( r ) r + r note: all items are from the previous column
ij i1 11 1j ij
Next, build the k=2 column:
2 1 1 * 1 1
r = r ( r ) r + r note: all items are from the previous column
ij i2 22 2j ij
Then, build the rest of the k=k columns:
k k-1 k-1 * k-1 k-1
r = r ( r ) r + r note: all items are from previous column
ij ik kk kj ij
Finally, for final states p, q, r the regular expression is
n n n
r + r + r
1p 1q 1r
Note that this is from a constructive proof that every NFA has a language
for which there is a corresponding regular expression.
Some minimization rules for regular expressions are available.
These can be applied at every step.
(Actually, extremely long equations, if not applied at every step.)
Note: phi is the empty set
epsilon is the zero length string
0, 1, a, b, c, are symbols in sigma
x is a variable or regular expression
( ... )( ... ) is concatenation
( ... ) + ( ... ) is union
( ... )* is the Kleene Closure = Kleene Star
(phi)(x) = (x)(phi) = phi
(epsilon)(x) = (x)(epsilon) = x
(phi) + (x) = (x) + (phi) = x
x + x = x
(epsilon)* = (epsilon)(epsilon) = epsilon
(x)* + (epsilon) = (x)* = x*
(x + epsilon)* = x*
x* (a+b) + (a+b) = x* (a+b)
x* y + y = x* y
(x + epsilon)x* = x* (x + epsilon) = x*
(x+epsilon)(x+epsilon)* (x+epsilon) = x*
Now for an example:
Given M=(Q, sigma, delta, q0, F) as
delta | a | b | c Q = { q1, q2}
--------+------+------+----- sigma = { a, b, c }
q1 | {q2} | {q2} | {q1} q0 = q1
--------+------+------+----- F = { q2}
q2 | phi | phi | phi
--------+------+------+-----
Informal method, draw state diagram:
/--\ a //--\\ a,b,c
-->| q1 |---->|| q2 ||-------->phi
\--/ b \\--//
^ |
| |c guess r = c* (a+b)
+--+ any number of c followed by a or b
phi stops looking at input
Formal method:
Remember r for k=0, means the regular expression directly from q1 to q1
11
| k=0
-----+-------------
r | c + epsilon from q1 input c goes to q1 (auto add epsilon
11 | when a state goes to itself)
-----+-------------
r | a + b from state q1 to q2, either input a or input b
12 |
-----+-------------
r | phi phi means no transition
21 |
-----+-------------
r | epsilon (auto add epsilon, a state can stay in that state)
22 |
-----+-------------
| k=0 | k=1 (building on k=0, using e for epsilon)
-----+-------------+------------------------------------
r | c + epsilon | (c+e)(c+e)* (c+e) + (c+e) = c*
11 | |
-----+-------------+------------------------------------
r | a + b | (c+e)(c+e)* (a+b) + (a+b) = c* (a+b)
12 | |
-----+-------------+------------------------------------
r | phi | phi (c+e)* (c+e) + phi = phi
21 | |
-----+-------------+------------------------------------
r | epsilon | phi (c+e)* (a+b) + e = e
22 | |
-----+-------------+------------------------------------
| k=0 | k=1 | k=2 (building on k=1,using minimized)
-----+-------------+----------+-------------------------
r | c + epsilon | c* |
11 | | |
-----+-------------+----------+-------------------------
r | a + b | c* (a+b) | c* (a+b)(e)* (e) + c* (a+b) only final
12 | | | state
-----+-------------+----------+-------------------------
r | phi | phi |
21 | | |
-----+-------------+----------+-------------------------
r | epsilon | e |
22 | | |
-----+-------------+----------+-------------------------
the final regular expression minimizes to r = c* (a+b)
Additional topics include Moore Machines and
Mealy Machines
HW4 is assigned
Review of Basics of Proofs.
The Pumping Lemma is generally used to prove a language is not regular.
If a DFA, NFA or NFA-epsilon machine can be constructed to exactly accept
a language, then the language is a Regular Language.
If a regular expression can be constructed to exactly generate the
strings in a language, then the language is regular.
If a regular grammar can be constructed to exactly generate the
strings in a language, then the language is regular.
To prove a language is not regular requires a specific definition of
the language and the use of the Pumping Lemma for Regular Languages.
A note about proofs using the Pumping Lemma:
Given: Formal statements A and B.
A implies B.
If you can prove B is false, then you have proved A is false.
For the Pumping Lemma, the statement "A" is "L is a Regular Language",
The statement "B" is a statement from the Predicate Calculus.
(This is a plain text file that uses words for the upside down A that
reads 'for all' and the backwards E that reads 'there exists')
Formal statement of the Pumping Lemma:
L is a Regular Language implies
(there exists n)(for all z)[z in L and |z|>=n implies
{(there exists u,v,w)(z = uvw and |uv|<=n and |v|>=1 and
i
(for all i>=0)(uv w is in L) )}]
The two commonest ways to use the Pumping Lemma to prove a language
is NOT regular are:
a) show that there is no possible n for the (there exists n),
this is usually accomplished by showing a contradiction such
as (n+1)(n+1) < n*n+n
b) show there is a way to partition z into u, v and w such that
i
uv w is not in L, typically by pumping a value i=0, i=1, or i=2.
i
Stop as soon as one uv w is not in the language,
thus, you have proved the language is not regular.
Note: The pumping lemma only applies to languages (sets of strings)
with infinite cardinality. A DFA can be constructed for any
finite set of strings. Use the regular expression to NFA 'union'
construction.
n n
Notation: the string having n a's followed by n b's is a b
which is reduced to one line by writing a^n b^n
Languages that are not regular:
L = { a^n b^n n>0 }
L = { a^f1(n) b^f2(n) n<c } for any non degenerate f1, f2.
L = { a^f(n) n>0 } for any function f(n)< k*n+c for all constants k and c
L = { a^(n*n) n>0 } also applies to n a prime(n log n), 2^n, n!
L = { a^n b^k n>0 k>n } can not save count of a's to check b's k>n
L = { a^n b^k+n n>0 k>1 } same language as above
Languages that are regular:
L = { a^n n>=0 } this is just r = a*
L = { a^n b^k n>0 k>0 } no relation between n and k, r = a a* b b*
L = { a^(37*n+511) n>0 } 511 states in series, 37 states in loop
You may be proving a lemma, a theorem, a corollary, etc
A proof is based on:
definition(s)
axioms
postulates
rules of inference (typical normal logic and mathematics)
To be accepted as "true" or "valid"
Recognized people in the field need to agree your
definitions are reasonable
axioms, postulates, ... are reasonable
rules of inference are reasonable and correctly applied
"True" and "Valid" are human intuitive judgments but can be
based on solid reasoning as presented in a proof.
Types of proofs include:
Direct proof (typical in Euclidean plane geometry proofs)
Write down line by line provable statements,
(e.g. definition, axiom, statement that follows from applying
the axiom to the definition, statement that follows from
applying a rule of inference from prior lines, etc.)
Proof by contradiction:
Given definitions, axioms, rules of inference
Assume Statement_A
use proof technique to derive a contradiction
(e.g. prove not Statement_A or prove Statement_B = not Statement_B,
like 1 = 2 or n > 2n)
Proof by induction (on Natural numbers)
Given a statement based on, say n, where n ranges over natural numbers
Prove the statement for n=0 or n=1
a) Prove the statement for n+1 assuming the statement true for n
b) Prove the statement for n+1 assuming the statement true for n in 1..n
Prove two sets A and B are equal, prove part 1, A is a subset of B
prove part 2, B is a subset of A
Prove two machines M1 and M2 are equal,
prove part 1 that machine M1 can simulate machine M2
prove part 2 that machine M2 can simulate machine M1
Limits on proofs:
Godel incompleteness theorem:
a) Any formal system with enough power to handle arithmetic will
have true theorems that are unprovable in the formal system.
(He proved it with Turing machines.)
b) Adding axioms to the system in order to be able to prove all the
"true" (valid) theorems will make the system "inconsistent."
Inconsistent means a theorem can be proved that is not accepted
as "true" (valid).
c) Technically, any formal system with enough power to do arithmetic
is either incomplete or inconsistent.
For reference, read through the automata definitions and
language definitions.
A class of languages is simply a set of languages with some
property that determines if a language is in the class (set).
The class of languages called regular languages is the set of all
languages that are regular. Remember, a language is regular if it is
accepted by some DFA, NFA, NFA-epsilon, regular expression or
regular grammar.
A single language is a set of strings over a finite alphabet and
is therefor countable. A regular language may have an infinite
number of strings. The strings of a regular language can be enumerated,
written down for length 0, length 1, length 2 and so forth.
But, the class of regular languages is the size of a power set
of any given regular language. This comes from the fact that
regular languages are closed under union. From mathematics we
know a power set of a countable set is not countable. A set that
is not countable, like the real numbers, can not be enumerated.
A class of languages is closed under some operation, op, when for any
two languages in the class, say L1 and L2, L1 op L2 is in the class.
This is the definition of "closed."
Summary. Regular languages are closed under operations: concatenation,
union, intersection, complementation, difference, reversal,
Kleene star, substitution, homomorphism and
any finite combination of these operations.
All of these operations are "effective" because there is an
algorithm to construct the resulting language.
Simple constructions include complementation by interchanging final
states and non final states in a DFA. Concatenation, union and Kleene
star are constructed using the corresponding regular expression to
NFA technique. Intersection is constructed using DeMorgan's theorem
and difference is constructed using L - M = L intersect complement M.
Reversal is constructed from a DFA using final states as starting states
and the starting state as the final state, reversing the direction
of all transition arcs.
We have seen that regular languages are closed under union because
the "+" is regular expressions yields a union operator for regular
languages. Similarly, for DFA machines, L(M1) union L(M2) is
L(M1 union M2) by the construction in lecture 6.
Thus we know the set of regular languages is closed under union.
In symbolic terms, L1 and L2 regular languages and L3 = L1 union L2
implies L3 is a regular language.
The complement of a language is defined in terms of set difference
__
from sigma star. L1 = sigma * - L1. The language L1 bar, written
as L1 with a bar over it, has all strings from sigma star except
the strings in L1. Sigma star is all possible strings over the
alphabet sigma. It turns out a DFA for a language can be made a
DFA for the complement language by changing all final states to
not final states and visa versa. (Warning! This is not true for NFA's)
Thus regular languages are closed under complementation.
Given union and complementation, by DeMorgan's Theorem,
L1 and L2 regular languages and L3 = L1 intersect L2 implies
______________
__ __
L3 is a regular language. L3 = ( L1 union L2) .
The construction of a DFA, M3, such that L(M3) = L(M1) intersect L(M2)
is given by:
Let M1 = (Q1, sigma, delta1, q1, F1)
Let M2 = (Q2, sigma, delta2, q2, F2)
Let S1 x S2 mean the cross product of sets S1 and S2, all ordered pairs,
Then
M3 = (Q1 x Q2, sigma, delta3, [q1,q2], F1 x F2)
where [q1,q2] is an ordered pair from Q1 x Q2,
delta3 is constructed from
delta3([x1,x2],a) = [delta1(x1,a), delta2(x2,a)] for all a in sigma
and all [x1,x2] in Q1 x Q2.
We choose to say the same alphabet is used in both machines, but this
works in general by picking the alphabet of M3 to be the intersection
of the alphabets of M1 and m2 and using all 'a' from this set.
Regular set properties:
One way to show that an operation on two regular languages produces a
regular language is to construct a machine that performs the operation.
Remember, the machines have to be DFA, NFA or NFA-epsilon type machines
because these machines have corresponding regular languages.
Consider two machines M1 and M2 for languages L1(M1) and L2(M2).
To show that L1 intersect L2 = L3 and L3 is a regular language we
construct a machine M3 and show by induction that M3 only accepts
strings that are in both L1 and L2.
M1 = (Q1, Sigma, delta1, q1, F1) with the usual definitions
M2 = (Q2, Sigma, delta2, q2, F2) with the usual definitions
Now construct M3 = (Q3, Sigma, delta3, q3, F3) defined as
Q3 = Q1 x Q2 set cross product
q3 = [q1,q2] q3 is an element of Q3, the notation means an ordered pair
Sigma = Sigma = Sigma we choose to use the same alphabet,
else some fix up is required
F3 = F1 x F2 set cross product
delta3 is constructed from
delta3([qi,qj],x) = [delta1(qi,x),delta2(qj,x)]
as you might expect, this is most easily performed on a DFA
The language L3(M3) is shown to be the intersection of L1(M1) and L2(M2)
by induction on the length of the input string.
For example:
M1: Q1 = {q0, q1}, Sigma = {a, b}, delta1, q1=q0, F1 = {q1}
M2: Q2 = {q3, q4, q5}, Sigma = {a, b}, delta2, q2=q3, F2 = {q4,q5}
delta1 | a | b | delta2 | a | b |
---+----+----+ -----+----+----+
q0 | q0 | q1 | q3 | q3 | q4 |
---+----+----+ -----+----+----+
q1 | q1 | q1 | q4 | q5 | q3 |
---+----+----+ -----+----+----+
q5 | q5 | q5 |
-----+----+----+
M3 now is constructed as
Q3 = Q1 x Q2 = {[q0,q3], [q0,q4], [q0,q5], [q1,q3], [q1,q4], [q1,q5]}
F3 = F1 x F2 = {[q1,q4], [q1,q5]}
initial state q3 = [q0,q3]
Sigma = technically Sigma_1 intersect Sigma_2
delta3 is constructed from delta3([qi,qj],x) = [delta1(qi,x),delta2(qj,x)]
delta3 | a | b |
---------+---------+---------+
[q0,q3] | [q0,q3] | [q1,q4] | this is a DFA when both
---------+---------+---------+ M1 and M2 are DFA's
[q0,q4] | [q0,q5] | [q1,q3] |
---------+---------+---------+
[q0,q5] | [q0,q5] | [q1,q5] |
---------+---------+---------+
[q1,q3] | [q1,q3] | [q1,q4] |
---------+---------+---------+
[q1,q4] | [q1,q5] | [q1,q3] |
---------+---------+---------+
[q1,q5] | [q1,q5] | [q1,q5] |
---------+---------+---------+
As we have seen before there may be unreachable states.
In this example [q0,q4] and [q0,q5] are unreachable.
It is possible for the intersection of L1 and L2 to be empty,
thus a final state will never be reachable.
Coming soon, the Myhill-Nerode theorem and minimization to
eliminate useless states.
Some sample DFA coded and run with dfa.cpp
n000.dfa complement of (0+1)*000(0+1)*
n000_dfa.out no 000 accepted
n2p1.dfa 2n+1 zeros n>0
n000_dfa.out 3, 5, 7 accepted
Decision algorithms for regular sets:
Remember: An algorithm must always terminate to be called an algorithm!
Basically, an algorithm needs to have four properties
1) It must be written as a finite number of unambiguous steps
2) For every possible input, only a finite number of steps
will be performed, and the algorithm will produce a result
3) The same, correct, result will be produced for the same input
4) Each step must have properties 1) 2) and 3)
Remember: A regular language is just a set of strings over a finite alphabet.
Every regular set can be represented by an regular expression
and by a minimized finite automata, a DFA.
We choose to use DFA's, represented by the usual M=(Q, Sigma, delta, q0, F)
There are countably many DFA's yet every DFA we look at has a finite
description. We write down the set of states Q, the alphabet Sigma,
the transition table delta, the initial state q0 and the final states F.
Thus we can analyze every DFA and even simulate them.
Theorem: The regular set accepted by DFA's with n states:
1) the set is non empty if and only if the DFA accepts at least one string
of length less than n. Just try less than |Sigma|^|Q| strings (finite)
2) the set is infinite if and only if the DFA accepts at least one string
of length k, n <= k < 2n. By pumping lemma, just more to try (finite)
Rather obviously the algorithm proceeds by trying the null string first.
The null string is either accepted or rejected in a finite time.
Then try all strings of length 1, i.e. each character in Sigma.
Then try all strings of length 2, 3, ... , k. Every try results in
an accept or reject in a finite time.
Thus we say there is an algorithm to decide if any regular set
represented by a DFA is a) empty, b) finite and c) infinite.
The practical application is painful! e.g. Given a regular expression,
convert it to a NFA, convert NFA to DFA, use Myhill-Nerode to get
a minimized DFA. Now we know the number of states, n, and the alphabet
Sigma. Now run the tests given in the Theorem above.
An example of a program that has not been proven to terminate is
terminates.c with output terminates.out
We will cover a program, called the halting problem, that no Turing
machine can determine if it will terminate.
Review for the quiz. (See homework WEB page.)
Open book. Open note, multiple choice in cs451q1.doc
Covers lectures and homework.
cp /afs/umbc.edu/users/s/q/squire/pub/download/cs451q1.doc . # your directory
libreoffice cs451q1.doc
or scp, winscp, to windows and use Microsoft word, winscp back to GL
save
exit
submit cs451 q1 cs451q1.doc
just view cs451q1.doc
See details on lectures, homework, automata and
formal languages using links below.
Open book so be sure you check on definitions and converting
from one definition (or abbreviation) to another.
Regular machine may be a DFA, NFA, NFA-epsilon
DFA deterministic finite automata
processes an input string (tape) and accepts or rejects
M = {Q, sigma, delta, q1, F}
Q set of states
sigma alphabet, list symbols 0,1 a,b,c etc
delta transition table
| 0 | 1 | etc
+----+----+
q1 | q2 | q3 | etc
+----+----+
q1 name of starting state
F list of names of final states
NFA nondeterministic finite automata
M = {Q, sigma, delta, q1, F}
delta transition table
| 0 | 1 | etc
+----+---------+
{q1,q3} | q2 | {q4,q5} | etc
+----+---------+
NFA nondeterministic finite automata with epsilon
M = {Q, sigma, delta, q1, F}
delta transition table
| 0 | 1 |epsilon| etc
+----+---------+-------+
{q1,q3} | q2 | {q4,q5} | q3 | etc
+----+---------+-------+
regular expression (defines strings accepted by DFA,NFA,NFA epsilon)
r1 = epsilon (computer input #e)
r2 = 0
r3 = ab
r4 = (a+b)c(a+b)
r5 = 1(0+1)*0(1*)0
regular language, a set of strings defined by a regular expression
from r1 {epsilon}
from r2 {0}
from r3 {ab}
from r4 {aca, acb, bca, bcb} finite
from r5 {epsilon,100,110110, ... } infinite
Myhill-Nerode theorem and minimization to eliminate useless states.
The Myhill-Nerode Theorem says the following three statements are equivalent:
1) The set L, a subset of Sigma star, is accepted by a DFA.
(We know this means L is a regular language.)
2) L is the union of some of the equivalence classes of a right
invariant(with respect to concatenation) equivalence relation
of finite index.
3) Let equivalence relation RL be defined by: xRLy if and only if
for all z in Sigma star, xz is in L exactly when yz is in L.
Then RL is of finite index.
The notation RL means an equivalence relation R over the language L.
The notation RM means an equivalence relation R over a machine M.
We know for every regular language L there is a machine M that
exactly accepts the strings in L.
Think of an equivalence relation as being true or false for a
specific pair of strings x and y. Thus xRy is true for some
set of pairs x and y. We will use a relation R such that
xRy <=> yRx x has a relation to y if and only if y has
the same relation to x. This is known as symmetric.
xRy and yRz implies xRz. This is known as transitive.
xRx is true. This is known as reflexive.
Our RL is defined xRLy <=> for all z in Sigma star (xz in L <=> yz in L)
Our RM is defined xRMy <=> xzRMyz for all z in Sigma star.
In other words delta(q0,xz) = delta(delta(q0,x),z)=
delta(delta(q0,y),z) = delta(q0,yz)
for x, y and z strings in Sigma star.
RM divides the set Sigma star into equivalence classes, one class for
each state reachable in M from the starting state q0. To get RL from
this we have to consider only the Final reachable states of M.
From this theorem comes the provable statement that there is a
smallest, fewest number of states, DFA for every regular language.
The labeling of the states is not important, thus the machines
are the same within an isomorphism. (iso=constant, morph=change)
Now for the algorithm that takes a DFA, we know how to reduce a NFA
or NFA-epsilon to a DFA, and produces a minimum state DFA.
-3) Start with a machine M = (Q, Sigma, delta, q0, F) as usual
-2) Remove from Q, F and delete all states that can not be reached from q0.
Remember a DFA is a directed graph with states as nodes. Thus use
a depth first search to mark all the reachable states. The unreachable
states, if any, are then eliminated and the algorithm proceeds.
-1) Build a two dimensional matrix labeling the right side q0, q1, ...
running down and denote this as the "p" first subscript.
Label the top as q0, q1, ... and denote this as the "q" second subscript
0) Put dashes in the major diagonal and the lower triangular part
of the matrix (everything below the diagonal). we will always use the
upper triangular part because xRMy = yRMx is symmetric. We will also
use (p,q) to index into the matrix with the subscript of the state
called "p" always less than the subscript of the state called "q".
We can have one of three things in a matrix location where there is
no dash. An X indicates a distinct state from our initialization
in step 1). A link indicates a list of matrix locations
(pi,qj), (pk,ql), ... that will get an x if this matrix location
ever gets an x. At the end, we will label all empty matrix locations
with a O. (Like tic-tac-toe) The "O" locations mean the p and q are
equivalent and will be the same state in the minimum machine.
(This is like {p,q} when we converted a NFA to a DFA. and is
the transitive closure just like in NFA to DFA.)
NOW FINALLY WE ARE READY for 1st Ed. Page 70, Figure 3.8 or
2nd Ed. Page 159.
1) For p in F and q in Q-F put an "X" in the matrix at (p,q)
This is the initialization step. Do not write over dashes.
These matrix locations will never change. An X or x at (p,q)
in the matrix means states p and q are distinct in the minimum
machine. If (p,q) has a dash, put the X in (q,p)
2) BIG LOOP TO END
For every pair of distinct states (p,q) in F X F do 3) through 7)
and for every pair of distinct states (p,q)
in (Q-F) x (Q-F) do 3) through 7)
(Actually we will always have the index of p < index of q and
p never equals q so we have fewer checks to make.)
3) 4) 5)
If for any input symbol 'a', (r,s) has an X or x then put an x at (p,q)
Check (s,r) if (r,s) has a dash. r=delta(p,a) and s=delta(q,a)
Also, if a list exists for (p,q) then mark all (pi,qj) in the list
with an x. Do it for (qj,pi) if (pi,qj) has a dash. You do not have
to write another x if one is there already.
6) 7)
If the (r,s) matrix location does not have an X or x, start a list
or add to the list (r,s). Of course, do not do this if r = s,
of if (r,s) is already on the list. Change (r,s) to (s,r) if
the subscript of the state r is larger than the subscript of the state s
END BIG LOOP
Now for an example, non trivial, where there is a reduction.
M = (Q, Sigma, delta, q0, F} and we have run a depth first search to
eliminate states from Q, F and delta that can not be reached from q0.
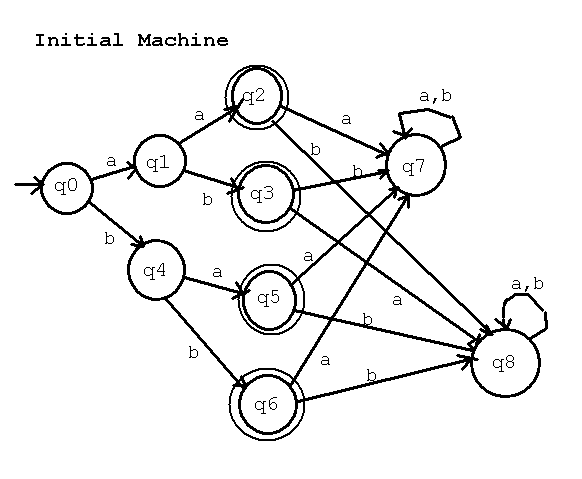
Q = {q0, q1, q2, q3, q4, q5, q6, q7, q8}
Sigma = {a, b}
q0 = q0
F = {q2, q3, q5, q6}
delta | a | b | note Q-F = {q0, q1, q4, q7, q8}
----+----+----+
q0 | q1 | q4 | We use an ordered F x F = {(q2, q3),
----+----+----+ (q2, q5),
q1 | q2 | q3 | (q2, q6),
----+----+----+ (q3, q5),
q2 | q7 | q8 | (q3, q6),
----+----+----+ (q5, q6)}
q3 | q8 | q7 |
----+----+----+ We use an ordered (Q-F) x (Q-F) = {(q0, q1),
q4 | q5 | q6 | (q0, q4),
----+----+----+ (q0, q7),
q5 | q7 | q8 | (q0, q8),
----+----+----+ (q1, q4),
q6 | q7 | q8 | (q1, q7),
----+----+----+ (q1, q8),
q7 | q7 | q7 | (q4, q7),
----+----+----+ (q4, q8),
q8 | q8 | q8 | (q7, q8)}
----+----+----+
Now, build the matrix labeling the "p" rows q0, q1, ...
and labeling the "q" columns q0, q1, ...
and put in dashes on the diagonal and below the diagonal
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | | | | | | | | |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | | | | | | | |
+---+---+---+---+---+---+---+---+---+
q2 | - | - | - | | | | | | |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | | | | | |
+---+---+---+---+---+---+---+---+---+
q4 | - | - | - | - | - | | | | |
+---+---+---+---+---+---+---+---+---+
q5 | - | - | - | - | - | - | | | |
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | | |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | |
+---+---+---+---+---+---+---+---+---+
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
Now fill in for step 1) (p,q) such that p in F and q in (Q-F)
{ (q2, q0), (q2, q1), (q2, q4), (q2, q7), (q2, q8),
(q3, q0), (q3, q1), (q3, q4), (q3, q7), (q3, q8),
(q5, q0), (q5, q1), (q5, q4), (q5, q7), (q5, q8),
(q6, q0), (q6, q1), (q6, q4), (q6, q7), (q6, q8)}
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | | X | X | | X | X | | |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | X | X | | X | X | | |
+---+---+---+---+---+---+---+---+---+
q2 | - | - | - | | X | | | X | X |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | X | | | X | X |
+---+---+---+---+---+---+---+---+---+
q4 | - | - | - | - | - | X | X | | |
+---+---+---+---+---+---+---+---+---+
q5 | - | - | - | - | - | - | | X | X |
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | X | X |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | |
+---+---+---+---+---+---+---+---+---+
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
Now fill in more x's by checking all the cases in step 2)
and apply steps 3) 4) 5) 6) and 7). Finish by filling in blank
matrix locations with "O".
For example (r,s) = (delta(p=q0,a), delta(q=q1,a)) so r=q1 and s= q2
Note that (q1,q2) has an X, thus (q0, q1) gets an "x"
Another from F x F (r,s) = (delta(p=q4,b), delta(q=q5,b)) so r=q6 and s=q8
thus since (q6, q8) has an X then (p,q) = (q4,q5) gets an "x"
It depends on the order of the choice of (p, q) in step 2) whether
a (p, q) gets added to a list in a cell or gets an "x".
Another (r,s) = (delta(p,a), delta(q,a)) where p=q0 and q=q8 then
s = delta(q0,a) = q1 and r = delta(q8,a) = q8 but (q1, q8) is blank.
Thus start a list in (q1, q8) and put (q0, q8) in this list.
[ This is what 7) says: put (p, q) on the list for (delta(p,a), delta(q,a))
and for our case the variable "a" happens to be the symbol "a".]
Eventually (q1, q8) will get an "x" and the list, including (q0, q8)
will get an "x'.
Performing the tedious task results in the matrix:
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | x | X | X | x | X | X | x | x |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | X | X | O | X | X | x | x | The "O" at (q1, q4) means {q1, q4}
+---+---+---+---+---+---+---+---+---+ is a state in the minimum machine
q2 | - | - | - | O | X | O | O | X | X |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | X | O | O | X | X | The "O" for (q2, q3), (q2, q5) and
+---+---+---+---+---+---+---+---+---+ (q2, q6) means they are one state
q4 | - | - | - | - | - | X | X | x | x | {q2, q3, q5, q6} in the minimum
+---+---+---+---+---+---+---+---+---+ machine. many other "O" just
q5 | - | - | - | - | - | - | O | X | X | confirm this.
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | X | X |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | O | The "O" in (q7, q8) means {q7, q8}
+---+---+---+---+---+---+---+---+---+ is one state in the minimum machine
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
The resulting minimum machine is M' = (Q', Sigma, delta', q0', F')
with Q' = { {q0}, {q1,q4}, {q2,q3,q5,q6}, {q7,q8} } four states
F' = { {q2,q3,q5,q6} } only one final state
q0' = q0
delta' | a | b |
----------+----------------+------------------+
{q0} | {q1,q4} | {q1,q4} |
----------+----------------+------------------+
{q1,q4} | {q2,q3,q5,q6} | {q2,q3,q5,q6} |
----------+----------------+------------------+
{q2,q3,q5,q6} | {q7,q8} | {q7,q8} |
----------+----------------+------------------+
{q7,q8} | {q7,q8} | {q7,q8} |
----------+----------------+------------------+
Note: Fill in the first column of states first. Check that every
state occurs in some set and in only one set. Since this is a DFA
the next columns must use exactly the state names found in the
first column. e.g. q0 with input "a" goes to q1, but q1 is now {q1,q4}
Use the same technique as was used to convert a NFA to a DFA, but
in this case the result is always a DFA even though the states have
the strange looking names that appear to be sets, but are just
names of the states in the DFA.
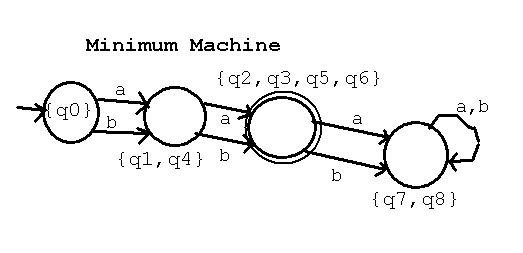
It is possible for the entire matrix to be "X" or "x" at the end.
In this case the DFA started with the minimum number of states.
At the heart of the algorithm is the following:
The sets Q-F and F are disjoint, thus the pairs of states (Q-F) X (F)
are distinguishable, marked X. For the pairs of states (p,q) and (r,s)
where r=delta(p,a) and s=delta(q,a) if p is distinguishable from q,
then r is distinguishable from s, thus mark (r,s) with an x.
If you do not wish to do minimizations by hand,
on linux.gl.umbc.edu use
ln -s /afs/umbc.edu/users/s/q/squire/pub/myhill myhill
myhill < your.dfa # result is in myhill_temp.dfa
or get the C++ source code from
/afs/umbc.edu/users/s/q/squire/pub/download/myhill.cpp
Instructions to compile are comments in source code
instruction on use are here
Grammars that have the same languages as DFA's
A grammar is defined as G = (V, T, P, S) where
V is a set of variables. We usually use capital letters for variables.
T is a set of terminal symbols. This is the same as Sigma for a machine.
P is a list of productions (rules) of the form:
variable -> concatenation of variables and terminals
S is the starting variable. S is in V.
A string z is accepted by a grammar G if some sequence of rules from P
can be applied to z with a result that is exactly the variable S.
We say that L(G) is the language generated (accepted) by the grammar G.
To start, we restrict the productions P to be of the form
A -> w w is a concatenation of terminal symbols
B -> wC w is a concatenation of terminal symbols
A, B and C are variables in V
and thus get a grammar that generates (accepts) a regular language.
Suppose we are given a machine M = (Q, Sigma, delta, q0, F) with
Q = { S }
Sigma = { 0, 1 }
q0 = S
F = { S }
delta | 0 | 1 |
---+---+---+
S | S | S |
---+---+---+
this looks strange because we would normally use q0 is place of S
The regular expression for M is (0+1)*
We can write the corresponding grammar for this machine as
G = (V, T, P, S) where
V = { S } the set of states in the machine
T = { 0, 1 } same as Sigma for the machine
P =
S -> epsilon | 0S | 1S
S = S the q0 state from the machine
the construction of the rules for P is directly from M's delta
If delta has an entry from state S with input symbol 0 go to state S,
the rule is S -> 0S.
If delta has an entry from state S with input symbol 1 go to state S,
the rule is S -> 1S.
There is a rule generated for every entry in delta.
delta(qi,a) = qj yields a rule qi -> a qj
An additional rule is generated for each final state, i.e. S -> epsilon
(An optional encoding is to generate an extra rule for every transition
to a final state: delta(qi,a) = any final state, qi -> a
with this option, if the start state is a final state, the production
S -> epsilon is still required. )
See g_reg.g file for worked example.
See g_reg.out for simulation check.
The shorthand notation S -> epsilon | 0S | 1S is the same as writing
the three rules. Read "|" as "or".
Grammars can be more powerful (read accept a larger class of languages)
than finite state machines (DFA's NFA's NFA-epsilon regular expressions).
i i
For example the language L = { 0 1 | i=0, 1, 2, ... } is not a regular
language. Yet, this language has a simple grammar
S -> epsilon | 0S1
Note that this grammar violates the restriction needed to make the grammars
language a regular language, i.e. rules can only have terminal symbols
and then one variable. This rule has a terminal after the variable.
A grammar for matching parenthesis might be
G = (V, T, P, S)
V = { S }
T = { ( , ) }
P = S -> epsilon | (S) | SS
S = S
We can check this be rewriting an input string
( ( ( ) ( ) ( ( ) ) ) )
( ( ( ) ( ) ( S ) ) ) S -> (S) where the inside S is epsilon
( ( ( ) ( ) S ) ) S -> (S)
( ( ( ) S S ) ) S -> (S) where the inside S is epsilon
( ( ( ) S ) ) S -> SS
( ( S S ) ) S -> (S) where the inside S is epsilon
( ( S ) ) S -> SS
( S ) S -> (S)
S S -> (S)
Thus the string ((()()(()))) is accepted by G because the rewriting
produced exactly S, the start variable.
More examples of constructing grammars from language descriptions:
Construct a CFG for non empty Palindromes over T = { 0, 1 }
The strings in this language read the same forward and backward.
G = ( V, T, P, S) T = { 0, 1 }, V = S, S = S, P is below:
S -> 0 | 1 | 00 | 11 | 0S0 | 1S1
We started the construction with S -> 0 and S -> 1
the shortest strings in the language.
S -> 0S0 is a palindrome with a zero added to either end
S -> 1S1 is a palindrome with a one added to either end
But, we needed S -> 00 and S -> 11 to get the even length
palindromes started.
"Non empty" means there can be no rule S -> epsilon.
n n
Construct the grammar for the language L = { a b n>0 }
G = ( V, T, P, S ) T = { a, b } V = { S } S = S P is:
S -> ab | aSb
Because n>0 there can be no S -> epsilon
The shortest string in the language is ab
a's have to be on the front, b's have to be on the back.
When either an "a" or a "b" is added the other must be added
in order to keep the count the same. Thus S -> aSb.
The toughest decision is when to stop adding rules.
In this case start "generating" strings in the language
S -> ab ab for n=1
S -> aSb aabb for n=2
S -> aaSbb aaabbb for n=3 etc.
Thus, no more rules needed.
"Generating" the strings in a language defined by a grammar
is also called "derivation" of the strings in a language.
Homework 6 is assigned
More theory, Context Free Grammar, see below what was a
state in a DFA is a variable, in a grammer, no states.
Given a grammar with the usual representation G = (V, T, P, S)
with variables V, terminal symbols T, set of productions P and
the start symbol from V called S.
Productions are variable, one or more variable, often | used
for more productions, rather than on seperate lines.
S -> aab
T -> aac | aad | epsilon
A derivation tree is constructed with
1) each tree vertex is a variable or terminal or epsilon
2) the root vertex is S
3) interior vertices are from V, leaf vertices are from T or epsilon
4) an interior vertex A has children, in order, left to right,
X1, X2, ... , Xk when there is a production in P of the
form A -> X1 X2 ... Xk
5) a leaf can be epsilon only when there is a production A -> epsilon
and the leafs parent can have only this child.
Watch out! A grammar may have an unbounded number of derivation trees.
It just depends on which production is expanded at each vertex.
For any valid derivation tree, reading the leafs from left to right
gives one string in the language defined by the grammar.
There may be many derivation trees for a single string in the language.
If the grammar is a CFG then a leftmost derivation tree exists
for every string in the corresponding CFL. There may be more than one
leftmost derivation trees for some string. See example below and
((()())()) example in previous lecture.
If the grammar is a CFG then a rightmost derivation tree exists
for every string in the corresponding CFL. There may be more than one
rightmost derivation tree for some string.
The grammar is called "ambiguous" if the leftmost (rightmost) derivation
tree is not unique for every string in the language defined by the grammar.
The leftmost and rightmost derivations are usually distinct but might
be the same.
Given a grammar and a string in the language represented by the grammar,
a leftmost derivation tree is constructed bottom up by finding a
production in the grammar that has the leftmost character of the string
(possibly more than one may have to be tried) and building the tree
towards the root. Then work on the second character of the string.
After much trial and error, you should get a derivation tree with a root S.
We will get to the CYK algorithm that does the parsing in a few lectures.
Examples: Construct a grammar for L = { x 0^n y 1^n z n>0 }
Recognize that 0^n y 1^n is a base language, say B
B -> y | 0B1 (The base y, the recursion 0B1 )
Then, the language is completed S -> xBz
using the prefix, base language and suffix.
(Note that x, y and z could be any strings not involving n)
G = ( V, T, P, S ) where
V = { B, S } T = { x, y, z, 0, 1 } S = S
P = S -> xBz
B -> y | 0B1
*
Now construct an arbitrary derivation for S => x00y11z
G
A derivation always starts with the start variable, S.
The "=>", "*" and "G" stand for "derivation", "any number of
steps", and "over the grammar G" respectively.
The intermediate terms, called sentential form, may contain
variable and terminal symbols.
Any variable, say B, can be replaced by the right side of any
production of the form B -> <right side>
A leftmost derivation always replaces the leftmost variable
in the sentential form. (In general there are many possible
replacements, the process is nondeterministic.)
One possible derivation using the grammar above is
S => xBz => x0B1z => x00B11z => x00y11z
The derivation must obviously stop when the sentential form
has only terminal symbols. (No more substitutions possible.)
The final string is in the language of the grammar. But, this
is a very poor way to generate all strings in the grammar!
A "derivation tree" sometimes called a "parse tree" uses the
rules above: start with the starting symbol, expand the tree
by creating branches using any right side of a starting
symbol rule, etc.
S
/ | \
/ | \
/ | \
/ | \
/ | \
x B z
/ | \
/ | \
/ | \
/ | \
0 B 1
/ | \
/ | \
0 B 1
|
y
Derivation ends x 0 0 y 1 1 z with all leaves
terminal symbols, a string in the language generated by the grammar.
More examples of grammars are:
G(L) for L = { x a^n y b^k z k > n > 0 }
note that there must be more b's than a's thus
B -> aybb | aBb | Bb
G = ( V, T, P, S ) where
V = { B, S } T = { a, b, x, y, z } S = S
P = S -> xBz B -> aybb | aBb | Bb
Incremental changes for "n > k > 0" B -> aayb | aBb | aB
Incremental changes for "n >= k >= 0" B -> y | aBb | aB
Independent exponents do not cause a problem when nested
equivalent to nesting parenthesis.
G(L) for L = { a^i b^j c^j d^i e^k f^k i>=0, j>=0, k>=0 }
| | | | | |
| +---+ | +---+
+-----------+
G = ( V, T , P, S )
V = { I, J, K, S } T = { a, b, c, d, e, f } S = S
P = S -> IK
I -> J | aId
J -> epsilon | bJc
K -> epsilon | eKf
G(L) for L = { a^i b^j c^k | any unbounded relation such as i=j=k>0, 0<i<k<j }
the G(L) can not be a context free grammar. Try it.
This will be intuitively seen in the push down automata and provable
with the pumping lemma for context free languages.
What is a leftmost derivation trees for some string?
It is a process that looks at the string left to right and
runs the productions backwards.
Here is an example, time starts at top and moves down.
Given G = (V, T, P, S) V={S, E, I} T={a, b, c} S=S P=
I -> a | b | c
E -> I | E+E | E*E
S -> E (a subset of grammar from book)
Given a string a + b * c
I
E
S derived but not used
I
E
[E + E]
E
S derived but not used
I
E
[E * E]
E
S done! Have S and no more input.
Left derivation tree, just turn upside down, delet unused.
S
|
E
/ | \
/ | \
/ | \
E * E
/ | \ |
E + E I
| | |
I I c
| |
a b
Check: Read leafs left to right, must be initial string, all in T.
Interior nodes must be variables, all in V.
Every vertical connection must be tracable to a production.
The goal here is to take an arbitrary Context Free Grammar
G = (V, T, P, S) and perform transformations on the grammar that
preserve the language generated by the grammar but reach a
specific format for the productions.
Overview: Step 1a) Eliminate useless variables that can not become terminals
Step 1b) Eliminate useless variables that can not be reached
Step 2) Eliminate epsilon productions
Step 3) Eliminate unit productions
Step 4) Make productions Chomsky Normal Form
Step 5) Make productions Greibach Normal Form
The CYK parsing uses Chomsky Normal Form as input
The CFG to NPDA uses Greibach Normal Form as input
Details: one step at a time
1a) Eliminate useless variables that can not become terminals
See 1st Ed. book p88, Lemma 4.1, figure 4.7
2nd Ed. section 7.1
Basically: Build the set NEWV from productions of the form
V -> w where V is a variable and w is one or more terminals.
Insert V into the set NEWV.
Then iterate over the productions, now accepting any variable
in w as a terminal if it is in NEWV. Thus NEWV is all the
variables that can be reduced to all terminals.
Now, all productions containing a variable not in NEWV
can be thrown away. Thus T is unchanged, S is unchanged,
V=NEWV and P may become the same or smaller.
The new grammar G=(V,T,P,S) represents the same language.
1b) Eliminate useless variables that can not be reached from S
See 1st Ed. book p89, Lemma 4.2, 2nd Ed. book 7.1.
Set V'=S, T'=phi, mark all production as unused.
Iterate repeatedly through all productions until no change
in V' or T'. For any production A -> w, with A in V'
insert the terminals from w into the set T' and insert
the variables form w into the set V' and mark the
production as used.
Now, delete all productions from P that are marked unused.
V=V', T=T', S is unchanged.
The new grammar G=(V,T,P,S) represents the same language.
2) Eliminate epsilon productions.
See 1st Ed. book p90, Theorem 4.3, 2nd Ed. book 7.1
This is complex. If the language of the grammar contains
the null string, epsilon, then in principle remove epsilon
from the grammar, eliminate epsilon productions.
The new grammar G=(V,T,P,S) represents the same language except
the new language does not contain epsilon.
3) Eliminate unit productions.
See 1st Ed. book p91, Theorem 4.4, 2nd Ed. 7.1
Iterate through productions finding A -> B type "unit productions".
Delete this production from P.
Make a copy of all productions B -> gamma, replacing B with A.
Be careful of A -> B, B -> C, C -> D type cases,
there needs to be copies of B -> gamma, C -> gamma, D -> gamma for A.
Delete duplicate productions. (sort and remove adjacent duplicate)
The new grammar G=(V,T,P,S) represents the same language.
Briefly, some pseudo code for the above steps.
Step 1a) The set V' = phi
loop through the productions, P, to find:
A -> w where w is all terminals
union V' with A
n := 0
while n /= |V'|
n := |V'|
loop through productions to find:
A -> alpha where alpha is only terminals and variables in V'
union V' with A
end while
Eliminate := V - V'
loop through productions
delete any production containing a variable in Eliminate,
V := V'
Step 1b) The set V' = {S}
The set T' = phi
n := 0
while n /= |V'| + |T'|
n := |V'| + |T'|
loop through productions to find:
A -> alpha where A in V'
union V' with variables in alpha
union T' with terminals in alpha
end while
loop through productions
delete any production containing anything outside V' T' and epsilon
V := V'
T := T'
Step 2) The set N = phi
n := -1
while n /= |N|
n = |N|
loop through productions to find:
A -> epsilon
union N with A
delete production
A -> alpha where no terminals in alpha and
all variables in alpha are in N
union N with A
delete production
end while
if S in N set null string accepted
loop through productions
A -> alpha where at least one variable in alpha in N
generate rules A -> alpha' where alpha'
is all combinations of eliminating the
variables in N
Step 3) P' := all non unit productions ( not A -> B )
U := all unit productions
loop through productions in U, |U| times, to find:
A -> A
ignore this
A -> B
loop through productions in P'
copy/substitute B -> gamma to A -> gamma in P'
P := P'
eliminate duplicate productions (e.g. sort and check i+i against i)
See link to "Turing machines and parsers."
The CYKP, CYK parser, has the above steps coded in C++ and with
"verbose 3" in the grammar file, most of the simplification is printed.
Of possible interest is a test case g_elim.g
input data to cykp and output g_elim.out
Chomsky Normal Form is used by the CYK algorithm to determine
if a string is accepted by a Context Free Grammar.
Step 4) in the overall grammar "simplification" process is
to convert the grammar to Chomsky Normal Form.
Productions can be one of two formats A -> a or A -> BC
The right side of the production is either exactly
one terminal symbol or exactly two variables.
The grammars must have the "simplification" steps 1), 2) and 3) out
of the way, that is 1) No useless variables, 2) No nullable variables and
3) no unit productions.
Step 4) of "simplification" is the following algorithm:
'length' refers to the number of variables plus terminal
symbols on the right side of a production.
Loop through the productions
For each production with length greater than 1 do
Replace each terminal symbol with a new variable and
add a production new variable -> terminal symbol.
Loop through the productions
For each production with length grater than 2 do
Replace two rightmost variables with a new variable and
add a production new variable -> two rightmost variables.
(Repeat - either on a production or loop until no replacements.)
Now the grammar, as represented by the productions, is in Chomsky
Normal Form. proceed with CYK.
An optimization is possible but not required, for any two productions
with the same right side, delete the second production and
replace all occurrences of the second productions left variable
with the left variable of the first production in all productions.
Example grammar:
G = (V, T, P, S) V={S,A} T={a,b} S=S
S -> aAS
S -> a
A -> SbA
A -> SS
A -> ba
First loop through productions (Check n>1)
S -> aAS becomes S -> BAS (B is the next unused variable name)
B -> a
S -> a stays S -> a
A -> SbA becomes A -> SCA (C is the next unused variable name)
C -> b
A -> SS stays A -> SS
A -> ba becomes A -> DE
D -> b
E -> a
Second loop through productions (Check n>2)
S -> BAS becomes S -> BF (F is the next unused variable)
F -> AS
B -> a stays B -> a
S -> a stays S -> a
A -> SCA becomes A -> SG
G -> CA
C -> b stays C -> b
A -> SS stays A -> SS
A -> DE stays A -> DE
D -> b stays D -> b
E -> a stays E -> a
Optimization is possible, B -> a, S -> a, E -> a can be replaced
by the single production S -> a (just to keep 'S')
and all occurrences of 'B' and 'E' get replaced by 'S'.
Similarly D -> b can be deleted, keeping the C -> b production and
substituting 'C' for 'D'.
Giving the reduced Chomsky Normal Form:
S -> SF
F -> AS
S -> a
A -> CG
G -> CA
C -> b
A -> SS
A -> CS
For a computer generated reduction, a different naming convention
was chosen (to aid in debugging). First, a terminal symbol "a"
was replaced the prefixing "T_", thus "a" becomes "T_a".
Once a substitution is made, that substitution is remembered
so that there will be at most |T| rules generated of the form
T_a -> a
When there are more that two variables on the right hand side of
a production, the new production is named "C_" concatenated with
the last two variables separated by an underscore.
This provides an easy reduction if the same two variables are
replaced more than once. The productions will be sorted and
duplicates will sort together and can be detected and eliminated quickly.
(In order to be completely safe, this algorithm requires that
no underscores were used in the initial grammar.)
An example uses g_elim.out shown
in the last lecture. Extracted and cleaned up,
here is the Chomsky portion.
after eliminate, sorted productions:
A -> a
B -> a
S -> A B
S -> a A
S -> a S a S a
S -> a S a a
S -> a a S a
S -> a a a
Chomsky 1, replace terminal with variable
Chomsky part 1, sorted productions:
A -> a
B -> a
S -> A B
S -> T_a A
S -> T_a S T_a S T_a
S -> T_a S T_a T_a
S -> T_a T_a S T_a
S -> T_a T_a T_a
T_a -> a
Chomsky 2, new production for each pair over two
Chomsky Part 2 generated productions
C_ST_a -> S T_a
C_T_aS -> T_a S
C_ST_a -> S T_a
C_T_aT_a -> T_a T_a
C_ST_a -> S T_a
C_ST_a -> S T_a
C_T_aS -> T_a S
C_T_aT_a -> T_a T_a
after Chomsky, sorted productions:
A -> a
B -> a
C_ST_a -> S T_a
C_T_aS -> T_a S
C_T_aT_a -> T_a T_a
S -> A B
S -> T_a A
S -> T_a C_ST_a
S -> T_a C_T_aS
S -> T_a C_T_aT_a
T_a -> a
after Chomsky, Variables:
A B C_ST_a C_T_aS C_T_aT_a S T_a
Terminals unchanged, S unchanged.
This simple structure for the productions makes
possible an efficient parser.
Greibach Normal Form of a CFG has all productions of the form
A ->aV Where 'A' is a variable, 'a' is exactly one terminal and
'V' is a string of none or more variables.
Every CFG can be rewritten in Greibach Normal Form.
This is step 5 in the sequence of "simplification" steps for CFG's.
Greibach Normal Form will be used to construct a PushDown Automata
that recognizes the language generated by a Context Free Grammar.
Starting with a grammar: G = ( V, T, P, S)
1a) Eliminate useless variables that can not become terminals
1b) Eliminate useless variables that can not be reached
2) Eliminate epsilon productions
3) Eliminate unit productions
4) Convert productions to Chomsky Normal Form
5) Convert productions to Greibach Normal Form using algorithm below:
Re-label all variables such that the names are A1, A2, ... , Am .
The notation A(j) refers to the variable named Aj .
New variables may be created with names B1, B2, ... referred to as B(j) .
Productions may be created and/or removed (a mechanical implementation
may use coloring to track processed, added and deleted productions.)
Step 1 (repeat until no productions are added, m-1 times at most)
begin (m is the number of variables, can change on each repeat)
for k := 1 to m do
begin
for j := 1 to k-1 do
for each production of the form A(k) -> A(j) alpha do
begin
for all productions A(j) -> beta do
add production A(k) -> beta alpha
remove production A(k) -> A(j) alpha
end;
end;
for each production of form A(k) -> A(k) alpha do
begin
add production b(k) -> alpha and B(k) -> alpha B(k)
remove production A(k) -> A(k) alpha
end;
for each production A(k) -> beta where beta does not begin A(K) do
add production A(k) -> beta B(k)
end;
Step 2 (sort productions and delete any duplicates )
Remove A -> A beta by creating B -> alpha B
Substitute so all rules become Greibach with starting terminal.
For neatness, sort productions and delete any duplicates
see book: 2nd Ed. page 271, section 7.1, Exercise 7.1.11 construction
Example (in file format, input given to program cykp,
output file greibach.pda)
// g1.g a test grammar
// G = (V, T, P, S) V={S,A} T={a,b} S=S
//
start S
terminal a b ;
verbose 7 // causes every step of ever loop to be printed
// runs a very long time !
S -> a A S ;
S -> a ;
A -> S b A ;
A -> S S ;
A -> b a ;
enddef
abaa
// greibach.pda , edited, from cykp < g1.g > g1_cykp.out
start S
terminal a ;
terminal b ;
variable A ;
variable C_AS ;
variable C_T_bA ;
variable S ;
variable T_a ;
A -> a C_AS C_T_bA ;
A -> a C_AS S ;
A -> a C_T_bA ;
A -> a S ;
A -> b T_a ;
C_AS -> a C_AS C_T_bA S ;
C_AS -> a C_AS S S ;
C_AS -> a C_T_bA S ;
C_AS -> a S S ;
C_AS -> b T_a S ;
C_T_bA -> b A ;
S -> a C_AS ;
S -> a ;
T_a -> a ;
enddef
Note that an optional optimization could delete the last rule,
and replace T_a by S.
Push Down Automata M = ( Q, Sigma, Gamma, delta, q0, Z0, F)
Q = a finite set of states including q0
Sigma = a finite alphabet of input symbols (on the input tape)
Gamma = a finite set of push down stack symbols including Z0
delta = a set of nondeterministic transitions
from-state tape-input top-of-stack to-state symbol(s)-to-push
q0 = the initial state, an element of Q
Z0 = the initial stack contents, an element of Gamma
F = the set of final accepting states, if empty then accept
on an empty stack at end of input
+-------------------------+
| input string |
+-------------------------+
^ read, move right
|
| read or write (pop or push)
+-------------------------------------> |Z0 |
| +-----+ | |
| | |--> accept | | push down
+--+ FSM | | | stack
| |--> reject | |
+-----+
accepts at end of input string, when in a final state,
and stack contains only Z0. Standard Finite State Machine
we have been using. The only extra part is the
push down stack.
Many parsers use a push down stack. We are covering the
basic abstract, theory, that can prove parsers work.
BNF Backus-Naur Form
history 4000BC to 1963
The similarity of our "productions" with the computer BNF is shown
in the following example.
Variables can be any string, we use uppercase letters and numbers.
Terminals are enclosed in apostrophes.
Colon, :, replaces arrow, ->
Vertical bar, |, is "or"
Computer BNF Production
file type .y file type .g
S : 'a' S -> a
| 'a' S S -> aS
S -> a | aS
term : var '*' var
T1 : V1 '*' V1 T1 -> V1*V1 when * in Sigma
B : B -> epsilon | Bab | Bb
| B 'a' B
| B 'b'
Additional actions/output/statements can be used in computer BNF, { stuff }
C : 'c'
{ printf("found a 'c' \n); }
| 'c" C
{ printf("here comes more 'c' \n); }
Thus, formatting, put "|" under ":". May also need or use ";"
big ugly "C" language example
Note needs "tokenizer" for variables and numbers,
punctuation are tokens, reserved words are tokens, ...
then rules, ...
Review for Quiz 2
See project description
A CFL that is inherently ambiguous is one for which no
unambiguous CFG can exists.
i i j j i j j i
L= {a b c d | i,j>0} union {a b c d | i,j>0} is such a language
i i j j
The productions for a b c d could be
1) S -> I J
2) I -> a b
3) I -> a I b
4) J -> c d
5) J -> c J d
i j j i
The productions for a b c d could be (using K instead of J)
6) S -> a K d
7) S -> a S d
8) K -> b c
9) K -> b K c
Now consider the case i = j. This is a string generated by both
grammars and thus will have two rightmost derivations.
(one involving I and J, and one involving K)
Thus ambiguous and not modifiable to make it unambiguous.
An ambiguous grammar is a grammar for a language where at least one
string in the language has two parse trees. This is equivalent to
saying some string has more than one leftmost derivation or more
than one rightmost derivation.
Similar to Quiz 1 Open book. Open note, multiple choice in cs451q2.doc Covers lectures and homework. cp /afs/umbc.edu/users/s/q/squire/pub/download/cs451q2.doc . # your directory libreoffice cs451q2.doc or scp, winscp, to windows and use Microsoft word, winscp back to GL save exit submit cs451 q2 cs451q2.doc See details on lectures, homework, automata and formal languages using links below.
Push Down Automata, PDA, are a way to represent the language class called
Context Free Languages, CFL, covered above. By themselves PDA's are not
very important but the hierarchy of Finite State Machines with
corresponding Regular Languages, PDA's with corresponding CFL's and
Turing Machines with corresponding Recursively Enumerable Sets (Languages),
is an important concept.
The definition of a Push Down Automata is:
M = (Q, Sigma, Gamma, delta, q0, Z0, F) where
Q = a finite set of states including q0
Sigma = a finite alphabet of input symbols (on the input tape)
Gamma = a finite set of push down stack symbols including Z0
delta = a group of nondeterministic transitions mapping
Q x (Sigma union {epsilon}) x Gamma to finite sets of Q x Gamma star
q0 = the initial state, an element of Q, possibly the only state
Z0 = the initial stack contents, an element of gamma, possibly the only
stack symbol
F = the set of final, accepting, states but may be empty for a PDA
"accepting on an empty stack"
Unlike finite automata, the delta is not presented in tabular form.
The table would be too wide. Delta is a list of, nondeterministic,
transitions of the form:
delta(q,a,A) = { (qi,gammai), (qj,gammaj), ...} where
q is the current state,
a is the input tape symbol being read, an element of Sigma union {epsilon}
A is the top of the stack being read,
The ordered pairs (q sub i, gamma sub i) are respectively the next state
and the string of symbols to be written onto the stack. The machine
is nondeterministic, meaning that all the pairs are executed causing
a branching tree of PDA configurations. Just like the branching tree
for nondeterministic finite automata except additional copies of the
pushdown stack are also created at each branch.
The operation of the PDA is to begin in state q0, read the symbol on the
input tape or read epsilon. If a symbol is read, the read head moves
to the right and can never reverse to read that symbol again.
The top of the stack is read by popping off the symbol.
Now, having a state, an input symbol and a stack symbol a delta transition
is performed. If there is no delta transition defined with these three
values the machine halts. If there is a delta transition with the (q,a,A)
then all pairs of (state,gamma) are performed. The gamma represents a
sequence of push down stack symbols and are pushed right to left onto
the stack. If gamma is epsilon, no symbols are pushed onto the stack. Then
the machine goes to the next state, q.
When the machine halts a decision is made to accept or reject the input.
If the last, rightmost, input symbol has not been read then reject.
If the machine is in a final state accept.
If the set of final states is empty, Phi, and the only symbol on the stack
is Z0, then accept. (This is the "accept on empty stack" case)
Now, using pictures we show the machines for FSM, PDA and TM
+-------------------------+----------------- DFA, NFA, NFA epsilon
| input string | accepts Regular Languages
+-------------------------+-----------------
^ read, move right
|
| +-----+
| | |--> accept
+--+ FSM | M = ( Q, Sigma, delta, q0, F)
| |--> reject
+-----+
+-------------------------+----------------- Push Down Automata
| input string |Z0 stack accepts Context Free Languages
+-------------------------+-----------------
^ read, move right ^ read and write (push and pop)
| |
+-----------------------+
| +-----+
| | |--> accept
+--+ FSM | M = ( Q, Sigma, Gamma, delta, q0, Z0, F)
| |--> reject
+-----+
+-------------------------+----------------- Turing Machine
| input string |BBBBBBBB ... accepts Recursively Enumerable
+-------------------------+----------------- Languages
^ read and write, move left and right
|
| +-----+
| | |--> accept
+--+ FSM | M = ( Q, Sigma, Gamma, delta, q0, B, F)
| |--> reject
+-----+
An example of a language that requires the PDA to be a NPDA,
Nondeterministic Push Down Automata,
is L = { w wr | w in Sigma and wr is w written backwards }
wwr.npda
// wwr.npda code an NPDA for:
// language { w wr | wr is string w in reverse order w = {0, 1} }
// CGF S -> 00 # strict form, must have even length
// S -> 11
// S -> 0S0
// S -> 1S1
//
// remember, nondeterministic, do all applicable transitions in parallel
// create multiple stacks as needed, some of the parallel may die
//
// NPDA = (Q, sigma, gamma, delta, Q0, Z0, F)
// Q = {q0, q1, q2} states
// sigma = {0, 1} input tape symbols (#e is empty string, epsilon)
// gamma = {0, 1, Z} stack symbols
// delta = {(Q x sigma x gamma_pop) to (Q x gamma_push) ...
// nondeterministic transitions
// Q0 = q0 starting state
// Z0 = Z starting stack symbol
// F = {q2} final state
start q0
final q2
stack Z // saves typing Z0, initially on stack
// state, input-read, top-of-stack-popped, go-to-state, push-on-stack
q0 0 Z q0 0Z // first 6 just push input onto stack
q0 1 Z q0 1Z
q0 0 0 q0 00
q0 0 1 q0 01
q0 1 0 q0 10
q0 1 1 q0 11
q0 #e Z q1 Z // these 3 keep trying to find middle, most die
q0 #e 0 q1 0 // tried after every input symbol
q0 #e 1 q1 1
q1 0 0 q1 #e // matching input to stack, has popped stack, no push
q1 1 1 q1 #e
q1 #e Z q2 Z // accept, done
enddef
tape 110001100011 // accept, w = 110001
tape 00000 // reject, odd number of input characters
Given a Context Free Grammar, CFG, in Greibach Normal Form, A -> aB1B2B3...
Construct an NPDA machine that accepts the same language as that grammar.
We are given G = ( V, T, P, S ) and must now construct
M = ( Q, Sigma, Gamma, delta, q0, Z0, F)
Q = {q} the one and only state!
Sigma = T
Gamma = V
delta is shown below
q0 = q
Z0 = S
F = Phi NPDA will "accept on empty stack"
Now, for each production in P (individual production, no vertical bars)
A -> a gamma constructs
| | |
| | +-------------+
| | |
+-----------+ | gamma is a possibly empty, sequence of
| | | symbols from Gamma
+---+ | |
| | |
V V V
delta(q, a, A) = {(q, gamma), more may come from other productions}
If gamma is empty, use epsilon as in (q, epsilon)
Finished!
An example: Given production Resulting delta #
C -> 0 C T delta(q, 0, C) = (q, CT) 1
C -> 0 T T delta(q, 0, C) = (q, TT) 2
S -> 0 C delta(q, 0, S) = (q, C) 3
S -> 0 T delta(q, 0, S) = (q, T) 4
T -> 1 delta(q, 1, T) = (q, #e) 5
NPDA running with input tape 0011 and initial stack S
0011 |S|
^ | |
delta #3 and #4 both apply, resulting in two stacks and advancing input
0011 |C| |T|
^ | | | |
delta #1 and #2 apply to the first stack, the second stack dies, advancing
0011 |C| |T| dies
^ |T| |T|
| | | |
delta #5 applies to the second stack, the first stack dies, advancing
0011 dies |T|
^ | |
delta #5 applies, the stack becomes empty and advance to beyond input
0011 | |
^ | |
accept input string.
Another conversion algorithm that uses more states, three to be exact,
is somewhat simpler.
We are given G = ( V, T, P, S ) and must now construct
M = ( Q, Sigma, Gamma, delta, q0, Z0, F)
Q = {q0, q1, q2}
Sigma = T
Gamma = V union {Z} where Z not in V (an extra symbol)
delta = Q x (Sigma union epsilon) x Gamma -> Q x Gamma shown below
q0 = q0
Z0 = Z (to get the NPDA started)
F = q2 the final accepting state
Two predefined transitions, the start and the accept are:
delta(q0, epsilon, Z) = { (q1, SZ) }
delta(q1, epsilon, Z) = { (q2, Z) }
For every rule in P , Greibach normal form, A -> aU generate
delta(q1, a, A) = { (q1, U) } union all other sets from (q1, a, A)
Note: The empty string must be removed to create Greibach normal form,
thus a grammar that initially accepted the empty string needs the
extra transition
delta(q0, epsilon, Z) = { (q2, Z) }
The conversion is proved to simulate a leftmost derivation.
Now you have everything you need to do HW7
Nondeterministic Push Down Automata, another machine.
see below and PDA
Given a NPDA M = ( Q, Sigma, Gamma, delta, q0, Z0, Phi) and
Sigma intersection Gamma = Phi,
Construct a CFG G = ( V, T, P, S )
Set T = Sigma
S = S
V = { S } union { [q,A,p] | q and p in Q and A in Gamma }
This can be a big set! q is every state with A every Gamma with
p every state. The cardinality of V, |V|=|Q|x|Gamma|x|Q|
Note that the symbology [q,A,p] is just a variable name.
(the states in the NPDA are renamed q0, q1, ... if necessary)
Construct the productions in two stages, the S -> , then the [q,A,p] ->
S -> [q0,Z0,qi] for every qi in Q (including q0) |Q| of these productions
[qi,A,qm+1] -> a[qj,B1,q2][q2,B2,q3][q3,B3,q4]...[qm,Bm,qm+1] is created
for each q2, q3, q4, ..., qm+1 in Q
for each a in Sigma union {epsilon}
for each A,B1,B2,B3,...,Bm in Gamma
such that there is a delta of the form
delta(qi,a,A) = { ...,(qj,B1B2B3...Bm), ...}
Note three degenerate cases:
delta(qi,a,A)=phi makes no productions
delta(qi,a,A)={(qj,epsilon)} makes [qi,A,qj] -> a
delta(qi,epsilon,A)={(qj,epsilon)} makes [qi,A,qj] -> epsilon
The general case:
Pictorially, given delta(qi,a,A)= (qj,B1B2) generate the set
| | | | | | for qk being every state,
+-------------+ | | | | | while qm+1 is every state
| +---------------+ | | |
| | | | | |
| | +--+ | | |
| | | +-------+ | |
| | | | +-------+ |
| | | | | |
V V V V V V
[qi,A,qm+1] -> a[qj,B1,qk][qk,B2,qm+1]
| | ^ ^
| | | |
| +---+ |
+--------------------------+
The book suggests to follow the chain of states starting with the right
sides of the S -> productions, then the new right sides of the [q,a,p] ->
productions. The correct grammar is built generating all productions.
Then the "simplification" can be applied to eliminate useless variables,
eliminate nullable variables, eliminate unit productions, convert to
Chomsky Normal Form, convert to Greibach Normal Form.
WOW! Now we have the Greibach Normal Form of a NPDA with any number of
states and we can convert this to a NPDA with just one state by the
construction in the previous lecture.
The important concept is that the constructions CFG to NPDA and NPDA to CFG
provably keep the same language being accepted. Well, to be technical,
The language generated by the CFG is exactly the language accepted by
the NPDA. Fixing up any technical details like renaming Gamma symbols
if Gamma intersection Sigma not empty and accepting or rejecting
the null string appropriately.
The reverse of the example in the previous lecture. |Q|=1 makes it easy.
Given: NPDA = (Q, Sigma, Gamma, delta, q0, Z0, F)
Q={q} Sigma={0,1} Gamma={C,S,T} q0=q Z0=S F=Phi
delta(q, 0, C) = (q, CT)
delta(q, 0, C) = (q, TT)
delta(q, 0, S) = (q, C)
delta(q, 0, S) = (q, T)
delta(q, 1, T) = (q, epsilon)
Build: G = (V, T, P , S)
V = { S, qCq, qSq, qTq } four variable names
T = Sigma = {0, 1} (dropping the previous punctuation [,,])
S = Z0 = S
S-> productions
S -> qSq Note! qSq is a single variable
just dropped the [,, ] symbols
other productions:
delta(q, 0, C) = (q, CT)
| | | | ||
+-----+ | | +----+ ||
|+----------+ |+------+|
|| | || +-+
|| | || |
qCq -> 0 qCq qTq was C -> 0 C T
| | | |
| +---+ |
+--------------------+
continue using same method on each delta:
qCq -> 0 qTq qTq
qSq -> 0 qCq
qSq -> 0 qTq
qTq -> 1 (epsilon becomes nothing)
Now, if you prefer, rename the variables to single letters
(assuming you have a big enough alphabet)
For this simple example qCq becomes just C, qSq becomes just S
and qTq becomes just T, thus the productions become:
C -> 0 C T
C -> 0 T T
S -> 0 C
S -> 0 T
T -> 1
This grammar is Greibach normal form for L(G)={0^n 1^n | n<0}
Now, working an example for another NPDA for this same language:
NPDA M = ( Q, Sigma, Gamma, delta, q0, Z0, Phi)
Q = { q0, q1 }
Sigma = { 0, 1 }
Gamma = { Z0, V0, V1 }
delta =
(q0,0,Z0) = (q0,V0) pop Z0 write V0 (for zero)
(q0,0,V0) = (q0,V0V0) add another V0 to stack
(q0,1,V0) = (q1,epsilon) pop a V0 for a one
(q1,1,V0) = (q1,epsilon) pop a V0 for each 1
accept on empty stack
Build: G = (V, T, P , S)
V = { S, see below in productions }
T = Sigma = {0, 1}
S = Z0 = S
S-> productions
S -> [q0,Z0,q0] (one for each state) P1
S -> [q0,Z0,q1] P2
delta productions
(q0,0,Z0) = (q0,V0) (one for each state)
[q0,Z0,q0] -> 0 [q0,V0,q0] P3
| |
+---------------+
[q0,Z0,q1] -> 0 [q0,V0,q1] P4
| |
+---------------+
(q0,0,V0) = (q0,V0V0) (two combinations of two states)
[q0,V0,q0] -> 0 [q0,V0,q0] [q0,V0,q0] P5
| | | |
| +----+ |
+--------------------------+
[q0,V0,q0] -> 0 [q0,V0,q1] [q1,V0,q0] P6
| | | |
| +----+ |
+--------------------------+
[q0,V0,q1] -> 0 [q0,V0,q0] [q0,V0,q1] P7
| | | |
| +----+ |
+--------------------------+
[q0,V0,q1] -> 0 [q0,V0,q1] [q1,V0,q1] P8
| | | |
| +----+ |
+--------------------------+
(q0,1,V0) = (q1,epsilon)
[q0,V0,q1] -> 1 P9
(q1,1,V0) = (q1,epsilon)
[q1,V0,q1] -> 1 P10
A a brief check, consider the string from the derivation
P2, P4, P9 that produces the string 01
P2, P4, P8, P9, P10 that produces the string 0011
M = ( Q, Sigma, Gamma, delta, q0, B, F)
Q = finite set of states including q0
Sigma = finite set of input symbols not including B
Gamma = finite set of tape symbols including Sigma and B
delta = transitions mapping Q x Gamma to Q x Gamma x {L,R}
q0 = initial state
B = blank tape symbol, initially on all tape not used for input
F = set of final states
+-------------------------+-----------------
| input string |BBBBB ... accepts Recursively Enumerable Languages
+-------------------------+-----------------
^ read and write, move left and right
|
| +-----+
| | |--> accept
+--+ FSM |
| |--> reject
+-----+
+-------------------------+-----------------
| input and output string |BBBBB ... computes partial recursive functions
+-------------------------+-----------------
^ read and write, move left and right
|
| +-----+
| | |
+--+ FSM |--> done (a delta [q,a]->[empty], but may never happen )
| |
+-----+
delta is a table or list of the form:
[qi, ai] -> [qj, aj, L] or [qi, ai] -> [qj, aj, R]
(optional [qi, ai] -> [qj, aj, N])
qi is the present state
ai is the symbol under the read/write head
qj is the next state
aj is written to the tape at the present position
L is move the read/write head left one position after the write
R is move the read/write head right one position after the write
N is optional no movement of the tape.
It is generally a pain to "program" a Turing machine. You have to
convert the algorithm into the list of delta transitions. The fallback
is to describe in English the steps that should be performed. The
amount of detail needed depends on the reader of the algorithm
accepting that there is an obvious way for the Turing machine to
perform your steps.
There are a lot of possible Turing machines and a useful technique
is to code Turing machines as binary integers. A trivial coding is
to use the 8 bit ASCII for each character in the written description
of a Turing machine concatenated into one long bit stream.
Having encoded a specific Turing machine as a binary integer, we
can talk about TMi as the Turing machine encoded as the number "i".
It turns out that the set of all Turing machines is countable and
enumerable.
Now we can construct a Universal Turing Machine, UTM, that takes
an encoded Turing machine on its input tape followed by normal
Turing machine input data on that same input tape. The Universal Turing
Machine first reads the description of the Turing machine on the
input tape and uses this description to simulate the Turing machines
actions on the following input data. Of course a UTM is a TM and can
thus be encoded as a binary integer, so a UTM can read a UTM from
the input tape, read a TM from the input tape, then read the input
data from the input tape and proceed to simulate the UTM that is
simulating the TM. Etc. Etc. Etc.
In a future lecture we will make use of the fact that a UTM can be
represented as an integer and can thus also be the input data on
the input tape.
For an example of programming a Turing Machine see Turing Machine simulator
Basically, any algorithm can be coded in a high order language,
or coded in assembly language,
or coded as a Turing Machine program,
or built out of digital logic.
A Turing Machine program is a bit-by-bit description of an algorithm.
Each program step, as in assembly language, is one simple operation.
But at a much lower level than any assembly language.
A Turing Machine program step is a 'delta' entry
[qi, ai] -> [qj, aj, move]
When in state qi, if the read head sees tape symbol ai,
then transition to state qj, writing symbol aj to the tape and
moving one tape position according to 'move' which can be
L for left, R for right, N for no move.
For computer input to a TM simulator, the five items are just
written with white space as a separator and an optional sixth
field that is a comment.
Special character pairs #b are used for one blank.
## is used for epsilon, nothing written to tape.
A sample computer input for an algorithm to add unary strings is:
// add.tm add unary strings of zeros
// input tape 000...00 000..00 blank separated, blank at end
// output tape 000...000 sum of zeros on input tape
start s0
halt s9 // use halt rather than 'final' when computing a result
limit 20
s0 0 s0 ## R skip over initial 0's delta 1
s0 #b s1 0 R write 0 over blank delta 2
s1 0 s1 ## R keep moving delta 3
s1 #b s2 ## L detect at end delta 4
s2 0 s9 #b R blank extra 0 delta 5
tape 000#b00#b should end with five zeros on tape
The simulation starts with the TM in state s0 and read head on
the first character.
+-----------
|000 00 ---- tape
+-----------
^
|
| read/write head position
TM in state s0
Thus, delta 1 applies. The new state is the same s0, nothing is
written to the tape and the head is moved one place right.
+-----------
|000 00 ---- tape
+-----------
^
|
| read/write head position
TM in state s0
Following the steps, delta 2 writes a zero over the blank and
goes to state s1.
When in state s1 and a zero is read from the tape, delta 3,
stay in state s1 and move one space right.
When in state s1 and a blank is read from the tape, delta 4,
go to state s2 and back up one space (now over last zero).
When in state s2 and a zero is read from the tape, delta 5,
go to the final state, s9, and write a blank over the zero.
Machine stops when no delta applies. If in a final state
when machine stops, the algorithm (program) finished
successfully.
+-----------
|00000 ---- tape
+-----------
^
|
| read/write head position
TM in state s9
What would happen if there was a '1' on the tape with the
above TM program? The machine would stop in a non-final state
which indicates no answer was computed (like segfault).
Turing Machine limitations:
A Turing Machine can only compute with natural numbers,
integers, no floating point.
The Church Turing Thesis, covered later, is believed
yet never proved mathematically.
video, LEGO Turing Machine
Use the "simplification" steps to get to a Chomsky Normal Form.
cyk comes from Cocke-Younger-Kasami algorithm
wikipedia cyk
We have used a lot of automata machines, one defined in reg.dfa
reg.dfa
This .dfa was converted to a grammar g_reg.g
g_reg.g
The .g files are used with cyk, cykp programs
Given a CFG grammar G in Chomsky Normal Form and a string x of length n
Group the productions of G into two sets
{ A | A -> a } target is a terminal
{ A | A -> BC } target is exactly two variables
V is a two dimensional matrix. Each element of the matrix is a set.
The set may be empty, denoted phi, or the set may contain one or
more variables from the grammar G. V can be n by n yet only part is used.
x[i] represents the i th character of the input string x
Parse x using G's productions
for i in 1 .. n
V[i,1] = { A | A -> x[i] }
for j in 2..n
for i in 1 .. n-j+1
{
V[i,j] = phi
for k in 1 .. j-1
V[i,j] = V[i,j] union { A | A -> BC where B in V[i,k]
and C in V[i+k,j-k]}
}
if S in V[1,n] then x is in CFL defined by G.
In order to build a derivation tree, a parse tree, you need to extend
the CYK algorithm to record
(variable, production number, from a index, from B index, from C index)
in V[i,j]. V[i,j] is now a set of five tuples.
Then find one of the (S, production number, from a, from B, from C)
entries in V[1,n] and build the derivation tree starting at the root.
Notes: The parse is ambiguous if there is more than one (S,...) in V[1,n]
Multiple levels of the tree may be built while working back V[*,k] to
V[*,k-1] and there may be more than one choice at any level if the
parse is ambiguous.
Example: given a string x = baaba
given grammar productions
A -> a S -> AB
B -> b S -> BC
C -> a A -> BA
B -> CC
C -> AB
V[i,j] i
1(b) 2(a) 3(a) 4(b) 5(a) string input
1 B A,C A,C B A,C
2 S,A B S,C S,A
j
3 phi B B
4 phi S,A,C
5 S,A,C
^
|_ accept
Derivation tree
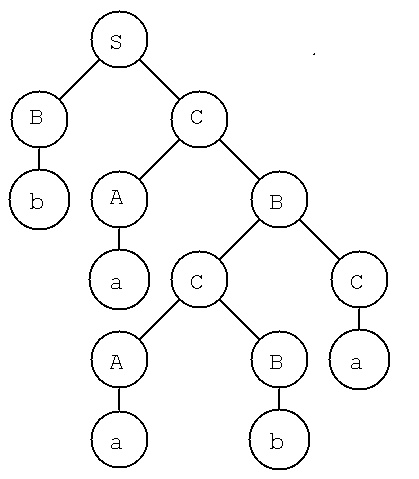 This can be a practical parsing algorithm.
But, not for large input. If you consider a computer language,
each token is treated as a terminal symbol. Typically punctuation
and reserved words are unique terminal symbols while all
numeric constants may be grouped as one terminal symbol and
all user names may be grouped as another terminal symbol.
The size problem is that for n tokens, the V matrix is 1/2 n^2
times the average number of CFG variables in each cell.
The running time is O(n^3) with a small multiplicative constant.
Thus, a 1000 token input might take 10 megabytes of RAM and
execute in about one second. But this would typically be only
a 250 line input, much smaller than many source files.
For computer languages the LALR1 and recursive descent parsers
are widely used.
For working small problems, given a CFG find if it generates
a specific string, use the available program cykp
Using the 'cykp' program on the sample grammar, trimming some,
the result was lect24.out
The input was lect24.g
Now HW8 is assigned
This can be a practical parsing algorithm.
But, not for large input. If you consider a computer language,
each token is treated as a terminal symbol. Typically punctuation
and reserved words are unique terminal symbols while all
numeric constants may be grouped as one terminal symbol and
all user names may be grouped as another terminal symbol.
The size problem is that for n tokens, the V matrix is 1/2 n^2
times the average number of CFG variables in each cell.
The running time is O(n^3) with a small multiplicative constant.
Thus, a 1000 token input might take 10 megabytes of RAM and
execute in about one second. But this would typically be only
a 250 line input, much smaller than many source files.
For computer languages the LALR1 and recursive descent parsers
are widely used.
For working small problems, given a CFG find if it generates
a specific string, use the available program cykp
Using the 'cykp' program on the sample grammar, trimming some,
the result was lect24.out
The input was lect24.g
Now HW8 is assigned
The Pumping Lemma is used to prove a language is not context free.
If a PDA machine can be constructed to exactly accept
a language, then the language is proved a Context Free Language.
PDA definition
If a Context Free Grammar can be constructed to exactly generate the
strings in a language, then the language is Context Free.
To prove a language is not context free requires a specific definition of
the language and the use of the Pumping Lemma for Context Free Languages.
A Context Free Language is a set of strings from a finite alphabet T.
The set may be finite or infinite for our use here. (not empty)
A grammar G = (V, T, P, S)
The productions P are restricted to:
not having an endless reduction loop with no reduction
V is a finite set of variables.
S is the starting variable from V
A note about proofs using the Pumping Lemma:
Given: Formal statements A and B.
A implies B.
If you can prove B is false, then you have proved A is false.
A B | A implies B
-----+------------
F F | T
F T | T (you can prove anything to be true with a false premise)
T F | F
T T | T
For the Pumping Lemma, the statement "A" is "L is a Context Free Language",
The statement "B" is a statement from the Predicate Calculus.
(This is a plain text file that uses words for the upside down A that
reads 'for all' and the backwards E that reads 'there exists')
Formal statement of the Pumping Lemma:
L is a Context Free Language implies
(there exists n)(for all z)[z in L and |z|>=n implies
{(there exists u,v,w,x,y)(z = uvwxy and |vwx|<=n and |vx|>=1 and
i i
(for all i>=0)(uv wx y is in L) )}]
The two commonest ways to use the Pumping Lemma to prove a language
is NOT context free are:
a) show that there is no possible n for the (there exists n),
this is usually accomplished by showing a contradiction such
as (n+1)(n+1) < n*n+n
b) show there is no way to partition some z into u,v,w,x,y such that
i i
uv wx y is in L, typically for a value i=0 or i=2.
Be sure to cover all cases by argument or enumerating cases.
[This gives a contradiction to the (for all z) clause.]
Some Context free languages and corresponding grammars:
i i
L={a b | i>=1} S->ab | aSb
2i 3i
L={a b | i>=1} S-> aabbb | aaSbbb [any pair of constants for 2,3]
i j i
L={a b c | i,j>=1} S->aBc | aSc B->b | bB
i i j
L={a b c | i,j>=1} S->DC D->ab | aDb C->c | cC
i i j j
L={a b a b | i,j>=1} S->CC C->ab | aCb
i i
L={ua wb y | i>=1 and u,w,y any fixed strings} S->uDy D->awb | aDb
R R
L={ww | w in Sigma star and w is w written backwards} S->xx | xSx
for all x in Sigma
Some languages that are NOT Context Free Languages
L={ww | w in Sigma star}
i i i
L={a b c | i>=1}
i j k
L={a b c | k > j > i >=1}
f(i) i
L={a b | i>=1} where f(i)=i**2 f(i) is the ith prime,
f(i) not bounded by a constant times i
meaning f(i) is not linear
i j i j
L={a b c d | i, j>=1}
You may be proving a lemma, a theorem, a corollary, etc
A proof is based on:
definition(s)
axioms
postulates
rules of inference (typical normal logic and mathematics)
To be accepted as "true" or "valid"
Recognized people in the field need to agree your
definitions are reasonable
axioms, postulates, ... are reasonable
rules of inference are reasonable and correctly applied
"True" and "Valid" are human intuitive judgments but can be
based on solid reasoning as presented in a proof.
Types of proofs include:
Direct proof (typical in Euclidean plane geometry proofs)
Write down line by line provable statements,
(e.g. definition, axiom, statement that follows from applying
the axiom to the definition, statement that follows from
applying a rule of inference from prior lines, etc.)
Proof by contradiction:
Given definitions, axioms, rules of inference
Assume Statement_A
use proof technique to derive a contradiction
(e.g. prove not Statement_A or prove Statement_B = not Statement_B,
like 1 = 2 or n > 2n)
Proof by induction (on Natural numbers)
Given a statement based on, say n, where n ranges over natural numbers
Prove the statement for n=0 or n=1
a) Prove the statement for n+1 assuming the statement true for n
b) Prove the statement for n+1 assuming the statement true for n in 1..n
Prove two sets A and B are equal, prove part 1, A is a subset of B
prove part 2, B is a subset of A
Prove two languages A and B are equal, prove part 1, A is a subset of B
prove part 2, B is a subset of A
Prove two machines M1 and M2 are equal,
prove part 1 that machine M1 can simulate machine M2
prove part 2 that machine M2 can simulate machine M1
Prove two grammars G1 and G2 are equal,
prove part 1 that grammar G1 can accept language of G2
prove part 2 that grammar G2 can accept language of G1
Limits on proofs:
Godel incompleteness theorem:
a) Any formal system with enough power to handle arithmetic will
have true theorems that are unprovable in the formal system.
(He proved it with Turing machines.)
b) Adding axioms to the system in order to be able to prove all the
"true" (valid) theorems will make the system "inconsistent."
Inconsistent means a theorem can be proved that is not accepted
as "true" (valid).
c) Technically, any formal system with enough power to do arithmetic
is either incomplete or inconsistent.
Now HW9 is assigned
Given two CFG's G1 = (V1, T1, P1, S1) for language L1(G1)
G2 = (V2, T2, P2, S2) for language L2(G2)
Rename variables until V1 intersect V2 is Phi.
We can easily get CFG's for the following languages:
L1 union L2 = L3(G3)
G3 = (V1 union V2 union {S3}, T1 union T2, P1+P2+P3, S3)
S3 -> S1 | S2
L1 concatenated L2 = L4(G4)
G4 = (V1 union V2 union {S4}, T1 union T2, P1+P2+P4, S4)
S4 -> S1S2
L1 star = L5(G5)
G5 = (V1 union V2 union {S5}, T1 union T2, P1+P2+P5, S5)
S5 -> S5S1 | epsilon
L2 substituted for terminal "a" in L1 = L6(G6)
G6 = (V1 union V2, T1-{a} union T2, P6+P2, S1)
P6 is P1 with every occurrence of "a" replaced with S2.
Notice that L1 intersect L2 may not be a CFG.
i i j i j i
Example: L1={a b c | i,j>0} L2={a b c | i,j>0} are CFG's
i i i
but L1 intersect L2 = {a b c | i>0} which is not a CFG.
The complement of L1 may not be a CFG.
The difference of two CFG's may not be a CFG.
The intersection of a Context Free Language with a Regular Language
is a Context Free Language.
As a supplement, the following shows how to take a CFG and possibly
use 'yacc' or 'bison' to build a parser for the grammar.
On GL man bison man yacc for instructions to run programs
The steps are to create a file xxx.y that includes the grammar,
and a file that is a main program that runs the parser.
An example grammar is coded in acfg.y
and a sample main program is coded in yymain.c
One possible set of commands to run the sample is:
bison acfg.y
gcc yymain.c acfg.tab.c
a.out
abaa
The output from this run shows the input being read and the rules
being applied:
read a
read b
read a
A -> ba
read a
read end of line \n converted to 0
S -> a
S -> aAS
accepted
A grammar that may be of more interest is a grammar for a calculator.
Simple statement such as
a=2
b=3
a+b
that prints the answer 5 can be coded as a CFG.
The following example uses bison format and has a simple lexical
analysis built in for single letter variables.
calc.y and a sample main program yymain.c
One possible set of commands to run calc is:
bison calc.y
gcc -o calc yymain.c calc.tab.c
calc
a=2
b=3
a+b
You should get the result 5 printed. See the grammar to find out what
other operations are available
The "Halting Problem" is a very strong, provably correct, statement
that no one will ever be able to write a computer program or design
a Turing machine that can determine if an arbitrary program will
halt (stop, exit) for every input.
This is NOT saying that some programs or some Turing machines can not
be analyzed to determine that they, for example, always halt.
The Halting Problem says that no computer program or Turing machine
can determine if ALL computer programs or Turing machines will halt
or not halt on ALL inputs. To prove the Halting Problem is
unsolvable we will construct one program and one input for which
there is no computer program or Turing machine that can correctly
determine if it halts or does not halt.
We will use very powerful mathematical concepts and do the proofs
for both a computer program and a Turing machine. The mathematical
concepts we need are:
Proof by contradiction. Assume a statement is true, show that the
assumption leads to a contradiction. Thus the statement is proved false.
Self referral. Have a computer program or a Turing machine operate
on itself, well, a copy of itself, as input data. Specifically we
will use diagonalization, taking the enumeration of Turing machines
and using TMi as input to TMi.
Logical negation. Take a black box that accepts input and outputs
true or false, put that black box in a bigger black box that
switches the output so it is false or true respectively.
The simplest demonstration of how to use these mathematical concepts
to get an unsolvable problem is to write on the front and back of
a piece of paper "The statement on the back of this paper is false."
Starting on side 1, you could choose "True" and thus deduce side 2
is "False". But staring at side 2, which is exactly the same as
side 1, you get that side 2 is "True" and thus side 1 is "False."
Since side 1, and side 2, can be both "True" and "False" there
is a contradiction. The problem of determining if sides 1 and 2 are
"True" of "False" is unsolvable. Sometimes called a paradox.
The Halting Problem for a programming language. We will use the "C"
programming language, yet any language will work.
Assumption: There exists a way to write a function named Halts such that:
int Halts(char * P, char * I)
{
/* code that reads the source code for a "C" program, P,
determines that P is a legal program, then determines if P
eventually halts (or exits) when P reads the input string I,
and finally sets a variable "halt" to 1 if P halts on input I,
else sets "halt" to 0 */
return halt;
}
Construct a program called Diagonal.c as follows:
int main()
{
char I[100000000]; /* make as big as you want or use malloc */
read_a_C_program_into( I );
if ( Halts(I,I) ) { while(1){} } /* loop forever, means does not halt */
else return 1;
}
Compile and link Diagonal.c into the executable program Diagonal.
Now execute
Diagonal < Diagonal.c
Consider two mutually exclusive cases:
Case 1: Halts(I,I) returns a value 1.
This means, by the definition of Halts, that Diagonal.c halts
when given the input Diagonal.c.
BUT! we are running Diagonal.c (having been compiled and linked)
and so we see that Halts(I,I) returns a value 1 causes the "if"
statement to be true and the "while(1){}" statement to be executed,
which never halts, thus our executing Diagonal.c does NOT halt.
This is a contradiction because this case says that Diagonal.c
does halt when given input Diagonal.c.
Well, try the other case.
Case 2: Halts(I,I) returns a value 0.
This means, by the definition of halts, that Diagonal.c does NOT
halt when given the input Diagonal.c.
BUT! we are running Diagonal.c (having been compiled and linked)
and so we see that Halts(I,I) returns a value 0 causes the "else"
to be executed and the main function halts (stops, exits).
This is a contradiction because this case says that Diagonal.c
does NOT halt when given input Diagonal.c.
There are no other cases, Halts can only return 1 or 0.
Thus what must be wrong is our assumption "there exists a way
to write a function named Halts..."
A example of a program that has not been proven to halt on all numbers
is terminates.c some cases terminates.out
Every Turing machine can be represented as a unique binary number.
Any method of encoding could be used. We can assume ASCII encoding of sample
s 0 space ... R
as 01110011 00110000 00100000 ... 01010010 just a big binary integer.
video, LEGO Turing Machine
The Halting Problem for Turing machines.
Assumption: There exists a Turing machine, TMh, such that:
When the input tape contains the encoding of a Turing machine, TMj followed
by input data k, TMh accepts if TMj halts with input k and TMh rejects
if TMj is not a Turing machine or TMj does not halt with input k.
Note that TMh always halts and either accepts or rejects.
Pictorially TMh is:
+----------------------------
| encoded TMj B k BBBBB ...
+----------------------------
^ read and write, move left and right
|
| +-----+
| | |--> accept
+--+ FSM | always halts
| |--> reject
+-----+
We now use the machine TMh to construct another Turing machine TMi.
We take the Finite State Machine, FSM, from TMh and
1) make none of its states be final states
2) add a non final state ql that on all inputs goes to ql
3) add a final state qf that is the accepting state
Pictorially TMi is:
+-------------------------------------------
| encoded TMj B k BBBBB ...
+-------------------------------------------
^ read and write, move left and right
|
| +----------------------------------+
| | __ |
| | / \ 0,1 |
| | +-| ql |--+ |
| | +-----+ | \___/ | |
| | | |--> accept-+ ^ | |
+--+-+ FSM | |_____| | may not halt
| | TMh |--> reject-+ _ |
| +-----+ | // \\ |
| +-||qf ||------|--> accept
| \\_// |
+----------------------------------+
We now have Turing machine TMi operate on a tape that has TMi as
the input machine and TMi as the input data.
+-------------------------------------------
| encoded TMi B encoded TMi BBBBB ...
+-------------------------------------------
^ read and write, move left and right
|
| +----------------------------------+
| | __ |
| | / \ 0,1 |
| | +-| ql |--+ |
| | +-----+ | \___/ | |
| | | |--> accept-+ ^ | |
+--+-+ FSM | |_____| | may not halt
| | |--> reject-+ _ |
| +-----+ | // \\ |
| +-||qf ||------|--> accept
| \\_// |
+----------------------------------+
Consider two mutually exclusive cases:
Case 1: The FSM accepts thus TMi enters the state ql.
This means, by the definition of TMh that TMi halts with input TMi.
BUT! we are running TMi on input TMi with input TMi
and so we see that the FSM accepting causes TMi to loop forever
thus NOT halting.
This is a contradiction because this case says that TMi
does halt when given input TMi with input TMi.
Well, try the other case.
Case 2: The FSM rejects thus TMi enters the state qf.
This means, by the definition of TMh that TMi does NOT halt with
input TMi.
BUT! we are running TMi on input TMi with input TMi
and so we see that the FSM rejecting cause TMi to accept and halt.
This is a contradiction because this case says that TMi
does NOT halt when given input TMi with input TMi.
There are no other cases, FSM either accepts or rejects.
Thus what must be wrong is our assumption "there exists a
Turing machine, TMh, such that..."
QED.
Thus we have proved that no Turing machine TMh can ever be created
that can be given the encoding of any Turing machine, TMj, and any input, k,
and always determine if TMj halts on input k.
Now HW10 is assigned
This is a mathematically unprovable belief that a reasonable intuitive definition of "computable" is equivalent to the list provably equivalent formal models of computation: Church Turing thesis Turing machines The "natural numbers" are what we in software call integer" Just adding 1 to a binary number on a Turing Machine takes: b_add1.tm Just adding two positive binary numbers on a Turing Machine takes: b_add.tm No sin, cos, exp in natural numbers, they need real numbers, float. Lambda Calculus Post Formal Systems Partial Recursive Functions Unrestricted Grammars Recursively Enumerable Languages (decision problems) and intuitively what is computable by a computer program written in any reasonable programming language.
Final Exam, cumulative, similar to Quiz 1 and Quiz 2. Some of the questions on previous exams may be asked again. Closed book. Multiple choice. Covers lectures and homework. See details on lectures, homework, automata and formal languages using links below. Grammar Definitions Formal Language Definitions Automata Definitions Computability Definitions
Open book. Open note, multiple choice in cs451fib.doc
Covers lectures and homework.
cp /afs/umbc.edu/users/s/q/squire/pub/download/cs451fin.doc . # your directory
libreoffice cs451fin.doc
or scp, winscp, to windows and use Microsoft word, winscp back to GL
save
exit
submit cs451 final cs451fin.doc
See details on lectures, homework, automata and
formal languages using links below.
1) go over the Quiz 1 and Quiz 2
the final exam will include some of these questions
2) You may find it helpful to go over the
Lecture Notes but not the details of constructions
3) Understand what classes of languages go with what machines (automata)
and grammars and regular expressions
4) Understand the statement of the Pumping Lemma for Context Free Languages
5) Understand the Halting Problem and why it is not computable
6) Understand the Church Turing Hypothesis
updated 5/8/2021
Last updated 6/16/12