Grammar Definitions
General
Type 0 Recursive
Type 1 Context Sensitive
Type 2 Context Free
Type 3 Regular
Derivation Tree
Parsing
Other Links
We define all grammars using the four tuple G = (V, T, P, S)
V is a finite set of variables, typically upper case letters,
and may have additional characters.
T is a finite set of terminal symbols, typically lower case letters,
and may be digits such as {0, 1} or other letters and digits.
Terminal symbols would be the tape alphabet in automata.
The intersection of V and T must be empty.
The zero length string, epsilon, may be used as a terminal symbol.
S is a distinguished element of V, the starting variable.
P are a finite set of productions written as alpha -> beta
where alpha and beta are sequences made up of the
elements of V and T. The types of grammars defined
below are restrictions on the content of alpha and beta.
Productions may be written one per line or may use
a short hand notation with the vertical bar | meaning "or".
S -> a
S -> aA
S -> BC
may be written as S -> a | aA | BC
using vertical line | for "or"
The Chomsky Hierarchy of Formal Languages 0, 1, 2, 3.
The class of recursive grammars has no restriction on
alpha and beta. An arbitrary example is:
S -> a | bb | A | aAbCcc | AABBcC
aSAB -> c | C | BaA | aAbBBccCCCd
ab -> c | ba | C | cBaAA | A
C -> epsilon | CC | AaBb
A -> B
Simplification rules may be available to eliminate
useless productions.
There may be variables that can not be reached from S.
There may be variables that can not become terminal symbols.
A Recursive Grammar defines the same class of languages as:
Recursive Languages
Turing Machines
A context sensitive grammar implies some alpha may not
be a single variable.
The restriction on a Type 0 grammar is that the length
of beta, right hand side, shall not be greater than
the length of alpha, left hand side.
For every production alpha -> beta
|beta| <= |alpha|
S -> a | A
AB -> cB | B | epsilon
aAb -> AaA | AA | A | a
A context free grammar implies alpha is a single variable.
S -> a | A | AB | aABb
A -> AB | ccBBaa
B -> BBB
All Context Free Grammars can be parsed by CYKP,
Cocke Younger Kasami parser
All Context Free Grammars can be converted to:
Chomsky Normal Form, productions V -> a V -> AB exactly two variables
Greibach Normal Form, productions V -> a V -> aW
a exactly one terminal, W any number of variables
A Context Free Grammar defines the same class of languages as:
NPDA Nondeterministic Push Down Automata
Conversion details in Lectures 21 and 22
CFG/CFL to NPDA
NPDA to CFG/CFL
The productions of a regular grammar are restricted to:
V -> a a single terminal
V -> aA a single terminal followed by a single variable
Conversion from a DFA to a regular grammar uses the states
of the DFA as variables and the alphabet of the DFA as
terminal symbols. The DFA delta transition table becomes
the productions.
a b
---+----+---
q0 | q1 | q2
q1 | q1 | q2
q2 | q2 | q1
renaming q0 to S, q1 to A, q2 to B
S -> aA
S -> bB
A -> aA | bB
B -> aB | bA
Additional rules are needed for final states.
If q2 is a file state, any transition to q2 gets a production
with only a terminal symbol.
S -> b
A -> b
B -> a
A Regular Grammar defines the same class of languages as:
Regular Languages
Regular Expressions
Finite Automata DFA, NFA, NFA-epsilon
The top-down tree for context free grammar:
The non leaf nodes of the derivation tree are labeled with
the variables of the grammar. The starting, root, node of
the tree is S. Unreachable variables will not appear in
the derivation tree.
The leaf nodes of the derivation tree are labeled with
the terminals of the grammar. Variables that can not
become terminals may appear as leaf nodes, yet may be
eliminated.
Great care must be taken to not keep repeating a
production. There may be a string of infinite length
in the grammar, and you would be drawing forever.
The goal is to end the tree with all leaf nodes
being terminal symbols.
There can be many different derivation trees for any
given grammar, based on the choice and order the
productions are drawn in the tree.
The leaf nodes, reading left to right, top to bottom,
give one string of terminal symbols that is in
the language of the grammar.
To start, chose one production of S -> ,
usually the longest or the one that has the most
variables.
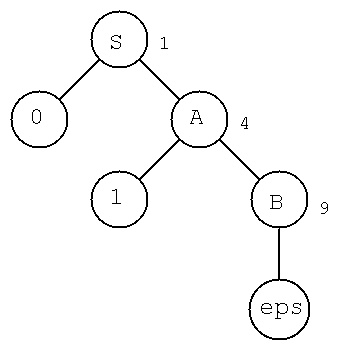
Example: (numbering the productions to annotate the tree)
1 S -> 0A
2 S -> 1S
3 A -> 0A
4 A -> 1B
5 B -> 0B
6 B -> 1B
7 B -> 0
8 B -> 1
9 B -> epsilon
This would have a DFA and regular expression definition:
| 0 | 1 use Q0 = S, Q1 = A, Q2 = B
---+----+--- start Q0, final Q2, sigma {0,1}
Q0 | Q1 | Q0
Q1 | Q1 | Q2 1* 0 0* 1 (0+1)* or
Q2 | Q2 | Q2 (0+1)* 01 (0+1)*
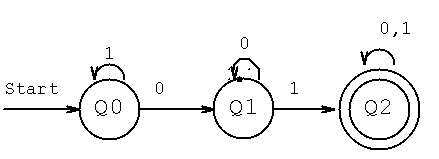 The smallest tree can be:
The smallest tree can be:
 A different derivation tree works bottom up,
starting with a string of terminal symbols from
the grammar as leaf nodes. If the string is in the
language of the grammar, there is a derivation tree
with a root node S. The tree is not necessarily unique.
Typically, find the left most terminal or string
of terminals that may be replaced by a variable.
Work up the tree, aiming for a root node of S.
Another typical method, is to work from the
right most terminal. If either method works,
it is provable that both will work.
This bottom up tree can be interpreted as a parse tree
when read top down. Given string 1101001 build
the derivation tree:
A different derivation tree works bottom up,
starting with a string of terminal symbols from
the grammar as leaf nodes. If the string is in the
language of the grammar, there is a derivation tree
with a root node S. The tree is not necessarily unique.
Typically, find the left most terminal or string
of terminals that may be replaced by a variable.
Work up the tree, aiming for a root node of S.
Another typical method, is to work from the
right most terminal. If either method works,
it is provable that both will work.
This bottom up tree can be interpreted as a parse tree
when read top down. Given string 1101001 build
the derivation tree:
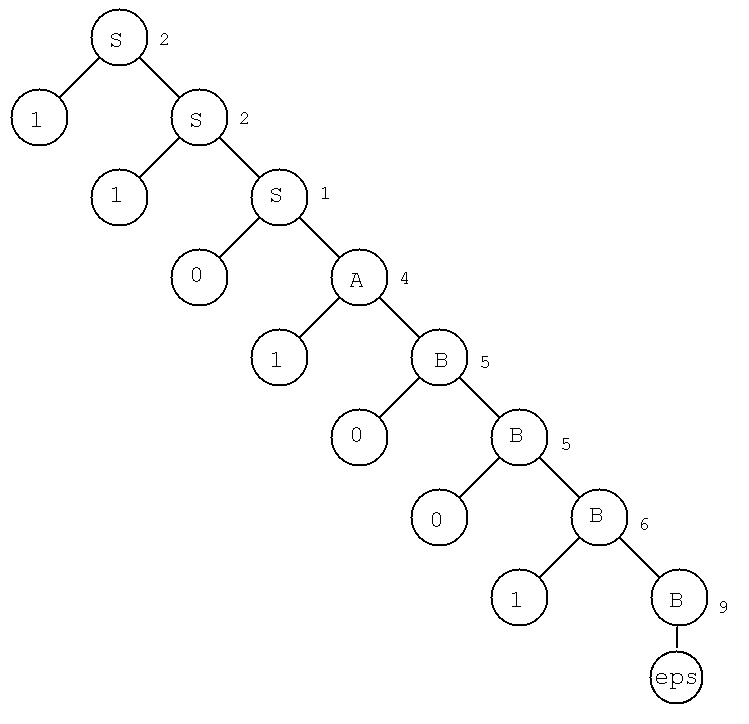
There are many parsing algorithms. For context free grammars,
that are converted to Chomsky Normal Form, the CYK algorithm
is typically used.
CYK algorithm on Wikipedia
Main reference:
Formal Languages and their Relation to Automata
Hopcroft and Ullman, Addison Wesley 1969
Last updated 4/10/21
 The smallest tree can be:
The smallest tree can be:
 A different derivation tree works bottom up,
starting with a string of terminal symbols from
the grammar as leaf nodes. If the string is in the
language of the grammar, there is a derivation tree
with a root node S. The tree is not necessarily unique.
Typically, find the left most terminal or string
of terminals that may be replaced by a variable.
Work up the tree, aiming for a root node of S.
Another typical method, is to work from the
right most terminal. If either method works,
it is provable that both will work.
This bottom up tree can be interpreted as a parse tree
when read top down. Given string 1101001 build
the derivation tree:
A different derivation tree works bottom up,
starting with a string of terminal symbols from
the grammar as leaf nodes. If the string is in the
language of the grammar, there is a derivation tree
with a root node S. The tree is not necessarily unique.
Typically, find the left most terminal or string
of terminals that may be replaced by a variable.
Work up the tree, aiming for a root node of S.
Another typical method, is to work from the
right most terminal. If either method works,
it is provable that both will work.
This bottom up tree can be interpreted as a parse tree
when read top down. Given string 1101001 build
the derivation tree:
