[syllabus] | [lecture notes] | [HW1-6,Q1] | [HW7-10,Q2,F] | [project]
[simulators/parsers] | [language definitions] | [automata definitions] | [computable definitions]
The most important item on all homework is YOUR USER NAME! All homework, project, quiz submitted on linux.gl.umbc.edu On linux use scp -p your.file your.computer:your_directory to move a file from GL to your computer. If your computer is Windows, use winscp to send file to linux.gl.umbc.edu/your_directory.
Homework must be submitted when due up to a week later. Do and turn in all homework, even if it is late. You must have homework file on GL and use submit command. If I can not read or understand your homework, you do not get credit. File types .txt .doc .png .jpg .pdf accepted.
Nice if you EMail only plain text! No word processor formats.
You may use a word processor or other software tools and
submit the results.
Use the same technique for plain text as is used in this WEB
page. Write out Greek letters, a plus means union in expressions,
a star after an expression is a Kleene star, see Language definitions
Just turn in two columns, column 1 has numbers 1 through 25, column 2 has a letter indicating your choice of the definition that best matches. These can be found in the two handouts: "Automata Definitions" and "Formal Language Definitions". 1. symbol 2. alphabet 3. string 4. formal language 5. regular language 6. regular expression 7. (0+1)* (00+11) 8. grammar 9. L(G) 10. L(M) 11. CFL 12. r.e. 13. finite automata 14. nondeterministic finite automata 15. pushdown automata 16. Turing machine 17. universal Turing machine 18. Mealy machine 19. Moore machine 20. NFA 21. TM 22. PDA 23. M(G) 24. M(L) 25. CYK Definition a. abbreviation for recursively enumerable b. abbreviation for Nondeterministic Finite Automata c. abbreviation for Context Free Language d. abbreviation for Turing Machine e. abbreviation for Cocke-Younger-Kasami algorithm f. a regular expression g. a machine defined by a language h. a machine defined by a grammar i. a Turing machine that simulates all other Turing machines j. a machine that outputs every time a state is entered k. a machine that outputs based on the input symbol and state l. a machine that uses a tape like a push down stack m. a language defined by a machine n. a language defined by a grammar o. a language representable by a finite automata p. a set of strings q. M = (Q, sigma, delta, q0, F) r. a finite automata with sets in its transition table s. an expression formed by concatenation, union and Kleene star t. finite set of symbols u. uninterpreted mark v. abbreviation for Push Down Automata w. a concatenation of symbols x. G = (V, T, P, S) y. a regular expression with all strings ending in 00 or 11 z. no other answer applies submit cs451 hw1 your.file
Be neat. Show your work. Partial credit will be given.
Remember: A set of strings is a Language.
For each language below, design a Deterministic Finite Automata, DFA.
a) Draw the state transition diagram.
b) Write the state transition table.
c) Write a regular expression.
Languages:
1) The set of strings over sigma={ 0, 1} ending in 00
2) The set of strings over sigma={ 0, 1} that contain three consecutive
ones.
3) The set of strings over sigma={ a, b, c} that contains the empty string
and strings that have a length that is a multiple of three
with every block of three containing one a, one b and one c
(implied, is in any order). Optional solution only abc order.
Be reasonable: You do not have to use the absolute minimum number
of states, but do not go overboard and use far more states than
are necessary. Regular expressions do not have to be minimized.
It is probably best if you do not try minimizations as this can
induce errors.
submit cs451 hw2 your.file
Unless otherwise stated, the first state is the starting state.
It is not necessary to remove unreachable states, yet, you may
remove unreachable states.
The constructive proof shows that every NFA can be converted to a DFA.
Be neat. Show your work. Partial credit will be given.
==============
1) Convert the NFA to an equivalent DFA (Answer the "?")
| 0 | 1 F = { q2, q4 }
----+----------+----------
q0 | {q0,q3} | {q0,q1}
q1 | phi | {q2}
q2 | {q2} | {q2}
q3 | {q4} | phi
q4 | {q4} | {q4}
M = (Q, sigma, delta, q0, F)
Q = { ? } You may simplify, you may use state names q00, q30, q01, q11
F = { ? } or other names with 9 or more states
q0 = ? optional to show phi as a state
sigma = { ? } you may use --->phi --->phi
delta = transition table ? 0 1 no circle
2) Convert NFA with epsilon moves to a DFA. (Answer the "?")
| 0 | 1 | 2 | eps F = { q2 }
-----+------+------+------+-------
q0 | {q0} | phi | phi | {q1}
q1 | phi | {q1} | phi | {q2}
q2 | phi | phi | {q2} | phi
M = (Q, sigma, delta, q0, F)
Q = { ? }
F = { ? }
q0 = ?
sigma = { ? }
delta = transition table ?
Hints and actually partial solutions are in WEB Page link below
or here Selected Lecture Notes, Lecture 4
submit cs451 hw3 your.file
You can draw small circles for diagrams, no state labels needed, but
make it neat so it can be graded. Show your work.
1) Convert a regular expression to a NFA-epsilon machine (diagram only)
1(0+1)* 0
2) Convert a regular expression to a NFA-epsilon machine (diagram only)
(0+1)* + (a+b)*
3) Convert machine given by delta transition table to a regular
expression. You do not have to minimize, but it may help you.
delta | a | b
----+----+---- q1 is the starting state
q1 | q2 | q1 q2 is the final state
q2 | q2 | q1
4) Convert machine given by delta transition table to a regular
expression. You do not have to minimize, but it may help you.
delta | a | b | c
----+------+-----+---- q1 is the starting state
q1 | q1 | phi | q3 q2 and q3 are the final state
q2 | phi | q2 | q3
q3 | q2 | q1 | q3
submit cs451 hw4 your.file
Open book, Open note. Multiple choice questions based on lectures, and homework. No cheating = no discussions with other students. Exam covers lectures: 3 - 10 Exam covers homework: HW1-HW3 Get exam cs451q1.doc (Be in your linux.gl directory) cp /afs/umbc.edu/users/s/q/squire/pub/download/cs451q1.doc . # your directory Mark your answers in .doc file. Put X after a) b) c) ... On linux.gl use libreoffice cs451q1.doc On Windows use scp, winscp to copy file and use Microsoft Word. submit cs451 q1 cs451q1.doc link, just to look at, do not use for quiz just look at quiz
State if the language is a regular set or not.
Prove you answer by a reasonable simple statement.
2n+1
1. { x | x is 0 and n>0 }
m n m+n
2. { x | x is 0 1 2 and m>0 and n>0 }
n
3. { x | x is 0 and n is a prime }
4. { x | x does not have three consecutive zeros, over the alphabet {0,1} }
5. { x | x has the same number of zeros and ones, over alphabet {0,1} }
R R
6. { x | x = y y , a Palindrome, y in (0+1)*, y is y written reversed }
7. What is the relationship between 1) the class of all regular sets and
2) the least class of languages closed under union, intersection
and complement containing all finite sets?
a) equal
b) first is a subset of second
c) second is a subset of first
d) non comparable
8. Find the minimum-state DFA for the state diagram shown below.
Hint: Selected Lecture Notes, Lecture 12
submit cs451 hw5 your.file
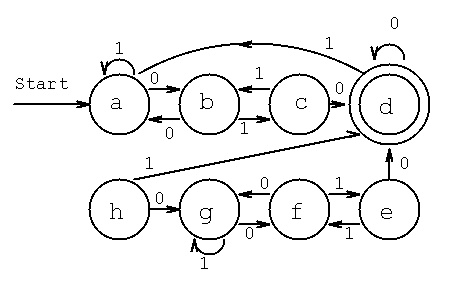
For the machine shown below:
1) M = (Q, Sigma, delta, q0, F)
Q = ?
Sigma = ?
delta = ?
q0 = ?
F = ?
2) L(M) = ? Use set notation L = { x | x is ??? }
3) give the grammar that has the same language as the machine shown below:
(Other than S, use state names as grammar variables.)
G = (V, T, P, S)
V = ?
T = ?
P = ?
S = ?
4) use the longest string in L(M) and show that the grammar accepts it.
(One way to do this is to write the string, then rewrite the string
each time a production applies, with the variable replacing its
pattern. The string is accepted if the result is the start variable)
submit cs451 hw6 yourfiles
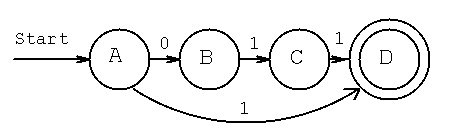
See Selected Lecture Notes, Lecture 13
Be neat. Show tables as tables. Show sets in { }
Last updated 3/13/2021