<- previous index next ->
Important! nondeterministic has nothing to do with random,
nondeterministic implies parallelism.
The difference between a DFA and a NFA is that the state transition
table, delta, for a DFA has exactly one target state but for a NFA has
a set, possibly empty (phi), of target states.
A NFA state diagram may have more than one line to get
to some state.
Example of a NFA, Nondeterministic Finite Automata given
by a) Machine Definition M = (Q, sigma, delta, q0, F)
b) Equivalent regular expression
c) Equivalent state transition diagram
and example tree of states for input string 0100011
and an equivalent DFA, Deterministic Finite Automata for the
first 3 states.
a) Machine Definition M = (Q, sigma, delta, q0, F)
Q = { q0, q1, q2, q3, q4 } the set of states
sigma = { 0, 1 } the input string alphabet
delta the state transition table
q0 = q0 the starting state
F = { q2, q4 } the set of final states (accepting when in
this state and no more input)
inputs
delta | 0 | 1 |
---------+---------+---------+
q0 | {q0,q3} | {q0,q1} |
q1 | phi | {q2} |
states q2 | {q2} | {q2} |
q3 | {q4} | phi |
q4 | {q4} | {q4} |
^ ^ ^
| | |
| +---------+-- a set of states, phi means empty set
+-- every state must be listed
b) The equivalent regular expression is (0+1)*(00+11)(0+1)*
This NFA represents the language L = all strings over {0,1} that
have at least two consecutive 0's or 1's.
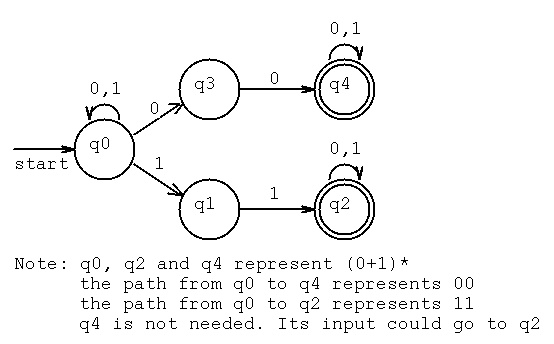
c) Equivalent NFA state transition diagram.
Note that state q3 does not go anywhere for an input of 1.
We use the terminology that the path "dies" if in q3 getting an input 1.
The tree of states this NFA is in for the input 0100011
input
q0
/ \ 0
q3 q0
dies / \ 1
q1 q0
dies / \ 0
q3 q0
/ / \ 0
q4 q3 q0
/ / / \ 0
q4 q4 q3 q0
/ / dies / \ 1
q4 q4 q1 q0
/ / / / \ 1
q4 q4 q2 q1 q0
^ ^ ^
| | |
accepting paths in NFA tree
Construct a DFA equivalent to the NFA above using just the first
three rows of delta (for brevity, consider q3 and q4 do not exists).
The DFA machine is M' = (Q', sigma, delta', q0', F')
The set of states is
Q' = 2**Q, the power set of Q = { phi, {q0}, {q1}, {q2}, {q0,q1}, {q0,q2},
{q1,q2}, {q0,q1,q2} }
Note the big expansion: If a set has n items, the power set has 2^n items.
Note: read the eight elements of the set Q' as names of states of M'
OK to use [ ] in place of { } if you prefer.
sigma is the same sigma = { 0, 1}
The state transition table delta' is given below
The starting state is set containing only q0 q0' = {q0}
The set of final states is a set of sets that contain q2
F' = { {q2}, {q0,q2}, {q1,q2}, {q0,q1,q2} }
Algorithm for building delta' from delta:
The delta' is constructed directly from delta.
Using the notation f'({q0},0) = f(q0,0) to mean:
in delta' in state {q0} with input 0 goes to the state
shown in delta with input 0. Take the union of all such states.
Further notation, phi is the empty set so phi union the set A is
just the set A.
Some samples: f'({q0,q1},0) = f(q0,0) union f(q1,0) = {q0}
f'({q0,q1},1) = f(q0,1) union f(q1,1) = {q0,q1,q2}
f'({q0,q2},0) = f(q0,0) union f(q2,0) = {q0,q2}
f'({q0,q2},1) = f(q0,1) union f(q2,1) = {q0,q1,q2}
sigma
delta | 0 | 1 | simplified for this construction
---------+---------+---------+
q0 | {q0} | {q0,q1} |
states q1 | phi | {q2} |
q2 | {q2} | {q2} |
sigma
delta' | 0 | 1 |
----------+-------------+-------------+
phi | phi | phi | never reached
{q0} | {q0} | {q0,q1} |
states {q1} | phi | {q2} | never reached
Q' {q2} | {q2} | {q2} | never reached
{q0,q1} | {q0} | {q0,q1,q2} |
{q0,q2} | {q0,q2} | {q0,q1,q2} |
{q1,q2} | {q2} | {q2} | never reached
{q0,q1,q2} | {q0,q2} | {q0,q1,q2} |
Note: Some of the states in the DFA may be unreachable yet
must be specified. Later we will use Myhill minimization.

DFA (not minimized) equivalent to lower branch of NFA above.
The sequence of states is unique for a DFA, so for the same input as
above 0100011 the sequence of states is
{q0} 0 {q0} 1 {q0,q1} 0 {q0} 0 {q0} 0 {q0} 1 {q0,q1}
1 {q0,q1,q2}
This sequence does not have any states involving q3 or q4 because just
a part of the above NFA was converted to a DFA. This DFA does not
accept the string 00 whereas the NFA above does accept 00.
Given a NFA and one or more strings, determine if the string(s)
are accepted by the NFA. This may be error prone and time
consuming to do by hand. Fortunately, there is a program
available to do this for you.
On linux.gl.umbc.edu do the following:
ln -s /afs/umbc.edu/users/s/q/squire/pub/nfa nfa
cp /afs/umbc.edu/users/s/q/squire/pub/download/fig2_7.nfa .
nfa < fig2_7.nfa # or nfa < fig2_7.nfa > fig2_7.out
NFA coded for simulation
You can code a Machine Definition into a data file for simulation
Q = { q0, q1, q2, q3, q4 }
sigma = { 0, 1 } // fig2_7.nfa
delta
q0 = q0 start q0
F = { q2, q4 } final q2
final q4
sigma
delta | 0 | 1 | q0 0 q0
---------+---------+---------+ q0 0 q3
q0 | {q0,q3} | {q0,q1} | q0 1 q0
q1 | phi | {q2} | q0 1 q1
states q2 | {q2} | {q2} | q1 1 q2
q3 | {q4} | phi | q2 0 q2
q4 | {q4} | {q4} | q2 1 q2
q3 0 q4
q4 0 q4
q4 1 q4
enddef
tape 10101010 // reject
tape 10110101 // accept
tape 10100101 // accept
tape 01010101 // reject
Full information is available at Simulators
The source code for the family of simulators is available.
<- previous index next ->

