<- previous index next ->
Given a regular expression, r , there is an associated regular language L(r).
Since there is a finite automata for every regular language,
there is a machine, M, for every regular expression such that L(M) = L(r).
The constructive proof provides an algorithm for constructing a machine, M,
from a regular expression r. The six constructions below correspond to
the cases:
1) The entire regular expression is the null string, i.e. L={epsilon}
(Any regular expression that includes epsilon will have the
starting state as a final state.)
r = epsilon
2) The entire regular expression is empty, i.e. L=phi r = phi
3) An element of the input alphabet, sigma, is in the regular expression
r = a where a is an element of sigma.
4) Two regular expressions are joined by the union operator, +
r1 + r2
5) Two regular expressions are joined by concatenation (no symbol)
r1 r2
6) A regular expression has the Kleene closure (star) applied to it
r*
The construction proceeds by using 1) or 2) if either applies.
The construction first converts all symbols in the regular expression
using construction 3).
Then working from inside outward, left to right at the same scope,
apply the one construction that applies from 4) 5) or 6).
 Example: Convert (00 + 1)* 1 (0 +1) to a NFA-epsilon machine.
Optimization hint: We use a simple form of epsilon-closure to combine
any state that has only an epsilon transition to another state, into
one state.
chose first 0 to get
Example: Convert (00 + 1)* 1 (0 +1) to a NFA-epsilon machine.
Optimization hint: We use a simple form of epsilon-closure to combine
any state that has only an epsilon transition to another state, into
one state.
chose first 0 to get
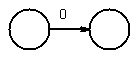 chose next 0, and concatenate
chose next 0, and concatenate
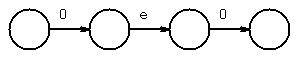 use epsilon-closure to combine states
use epsilon-closure to combine states
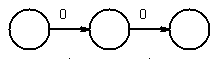 Chose 1, then added union
Chose 1, then added union
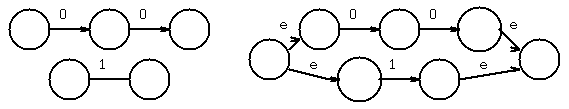 Apply Kleene star
Apply Kleene star
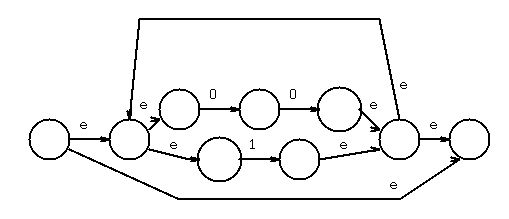 Chose 1, concatenate, combine states
Chose 1, concatenate, combine states
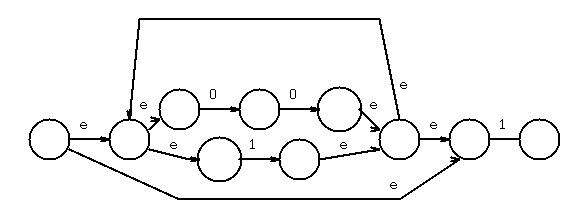 Concatenate (0+1), combine one state
Concatenate (0+1), combine one state
 The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4 in 1st Ed. or section 4.4 in 2nd Ed.
This will provide a DFA that has the minimum number of states.
Within a renaming of the states and reordering of the delta, state
transition table, all minimum machines of a DFA are identical.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
Example: r = (0+1)* (00+11) (0+1)*
Solution: find the primary operator(s) that are concatenation or union.
In this case, the two outermost are concatenation, giving, crudely:
//---------------\ /----------------\\ /-----------------\
-->|| <> M((0+1)*) <> |->| <> M((00+11)) <> ||->| <> M((0+1)*) <<>> |
\\---------------/ \----------------// \-----------------/
There is exactly one start "-->" and exactly one final state "<<>>"
The unlabeled arrows should be labeled with epsilon.
Now recursively decompose each internal regular expression.
The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4 in 1st Ed. or section 4.4 in 2nd Ed.
This will provide a DFA that has the minimum number of states.
Within a renaming of the states and reordering of the delta, state
transition table, all minimum machines of a DFA are identical.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
Example: r = (0+1)* (00+11) (0+1)*
Solution: find the primary operator(s) that are concatenation or union.
In this case, the two outermost are concatenation, giving, crudely:
//---------------\ /----------------\\ /-----------------\
-->|| <> M((0+1)*) <> |->| <> M((00+11)) <> ||->| <> M((0+1)*) <<>> |
\\---------------/ \----------------// \-----------------/
There is exactly one start "-->" and exactly one final state "<<>>"
The unlabeled arrows should be labeled with epsilon.
Now recursively decompose each internal regular expression.
<- previous index next ->
 Example: Convert (00 + 1)* 1 (0 +1) to a NFA-epsilon machine.
Optimization hint: We use a simple form of epsilon-closure to combine
any state that has only an epsilon transition to another state, into
one state.
chose first 0 to get
Example: Convert (00 + 1)* 1 (0 +1) to a NFA-epsilon machine.
Optimization hint: We use a simple form of epsilon-closure to combine
any state that has only an epsilon transition to another state, into
one state.
chose first 0 to get
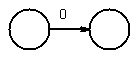 chose next 0, and concatenate
chose next 0, and concatenate
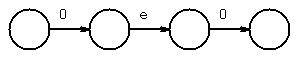 use epsilon-closure to combine states
use epsilon-closure to combine states
 Chose 1, then added union
Chose 1, then added union
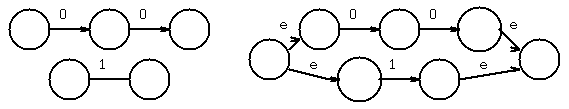 Apply Kleene star
Apply Kleene star
 Chose 1, concatenate, combine states
Chose 1, concatenate, combine states
 Concatenate (0+1), combine one state
Concatenate (0+1), combine one state
 The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4 in 1st Ed. or section 4.4 in 2nd Ed.
This will provide a DFA that has the minimum number of states.
Within a renaming of the states and reordering of the delta, state
transition table, all minimum machines of a DFA are identical.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
Example: r = (0+1)* (00+11) (0+1)*
Solution: find the primary operator(s) that are concatenation or union.
In this case, the two outermost are concatenation, giving, crudely:
//---------------\ /----------------\\ /-----------------\
-->|| <> M((0+1)*) <> |->| <> M((00+11)) <> ||->| <> M((0+1)*) <<>> |
\\---------------/ \----------------// \-----------------/
There is exactly one start "-->" and exactly one final state "<<>>"
The unlabeled arrows should be labeled with epsilon.
Now recursively decompose each internal regular expression.
The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4 in 1st Ed. or section 4.4 in 2nd Ed.
This will provide a DFA that has the minimum number of states.
Within a renaming of the states and reordering of the delta, state
transition table, all minimum machines of a DFA are identical.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
Example: r = (0+1)* (00+11) (0+1)*
Solution: find the primary operator(s) that are concatenation or union.
In this case, the two outermost are concatenation, giving, crudely:
//---------------\ /----------------\\ /-----------------\
-->|| <> M((0+1)*) <> |->| <> M((00+11)) <> ||->| <> M((0+1)*) <<>> |
\\---------------/ \----------------// \-----------------/
There is exactly one start "-->" and exactly one final state "<<>>"
The unlabeled arrows should be labeled with epsilon.
Now recursively decompose each internal regular expression.