<- previous index next ->
Use the "simplification" steps to get to a Chomsky Normal Form.
cyk comes from Cocke-Younger-Kasami algorithm
wikipedia cyk
We have used a lot of automata machines, one defined in reg.dfa
reg.dfa
This .dfa was converted to a grammar g_reg.g
g_reg.g
The .g files are used with cyk, cykp programs
Given a CFG grammar G in Chomsky Normal Form and a string x of length n
Group the productions of G into two sets
{ A | A -> a } target is a terminal
{ A | A -> BC } target is exactly two variables
V is a two dimensional matrix. Each element of the matrix is a set.
The set may be empty, denoted phi, or the set may contain one or
more variables from the grammar G. V can be n by n yet only part is used.
x[i] represents the i th character of the input string x
Parse x using G's productions
for i in 1 .. n
V[i,1] = { A | A -> x[i] }
for j in 2..n
for i in 1 .. n-j+1
{
V[i,j] = phi
for k in 1 .. j-1
V[i,j] = V[i,j] union { A | A -> BC where B in V[i,k]
and C in V[i+k,j-k]}
}
if S in V[1,n] then x is in CFL defined by G.
In order to build a derivation tree, a parse tree, you need to extend
the CYK algorithm to record
(variable, production number, from a index, from B index, from C index)
in V[i,j]. V[i,j] is now a set of five tuples.
Then find one of the (S, production number, from a, from B, from C)
entries in V[1,n] and build the derivation tree starting at the root.
Notes: The parse is ambiguous if there is more than one (S,...) in V[1,n]
Multiple levels of the tree may be built while working back V[*,k] to
V[*,k-1] and there may be more than one choice at any level if the
parse is ambiguous.
Example: given a string x = baaba
given grammar productions
A -> a S -> AB
B -> b S -> BC
C -> a A -> BA
B -> CC
C -> AB
V[i,j] i
1(b) 2(a) 3(a) 4(b) 5(a) string input
1 B A,C A,C B A,C
2 S,A B S,C S,A
j
3 phi B B
4 phi S,A,C
5 S,A,C
^
|_ accept
Derivation tree
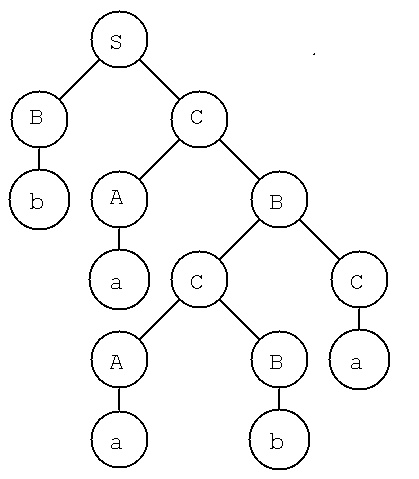This can be a practical parsing algorithm.
But, not for large input. If you consider a computer language,
each token is treated as a terminal symbol. Typically punctuation
and reserved words are unique terminal symbols while all
numeric constants may be grouped as one terminal symbol and
all user names may be grouped as another terminal symbol.
The size problem is that for n tokens, the V matrix is 1/2 n^2
times the average number of CFG variables in each cell.
The running time is O(n^3) with a small multiplicative constant.
Thus, a 1000 token input might take 10 megabytes of RAM and
execute in about one second. But this would typically be only
a 250 line input, much smaller than many source files.
For computer languages the LALR1 and recursive descent parsers
are widely used.
For working small problems, given a CFG find if it generates
a specific string, use the available program cykp
Using the 'cykp' program on the sample grammar, trimming some,
the result was lect24.out
The input was lect24.g
Now HW8 is assigned
<- previous index next ->