<- previous index next ->
lecture student4D.txt
program student4D.java
output student4D.out
Library of "44" four dimensional software
datread44.java
datwrite44.java
plot44.java
dat_scale44.java
dat_scale44.java
tri_split44.java
Some 44 .dat graphics data files:
Makefile that builds 44 applications and uses 44 .dat files:
A first cut at 4D, four dimensional rendering, uses 5 by 5 matrices:
Note that there are now eight (8) degrees of freedom:
Move in X, Y, Z, W and rotations about each axis (split into 6 matrices)
 Notation: x is left and right.
y is up and down
z is forward and back
w is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
Notation: x is left and right.
y is up and down
z is forward and back
w is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
 Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, w
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, w
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
4D sphere
 4th dimension smaller
4th dimension smaller
User control for plotting any two of x, y, z, t
against the value of function u(x,y,z,t)
source code plot_4d.java
 source code plot4d_gl.c
plot4d data generator f4d.c
source code plot4d_gl.c
plot4d data generator f4d.c

 Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.
Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.
octrahedron in 3D and increased to 4D
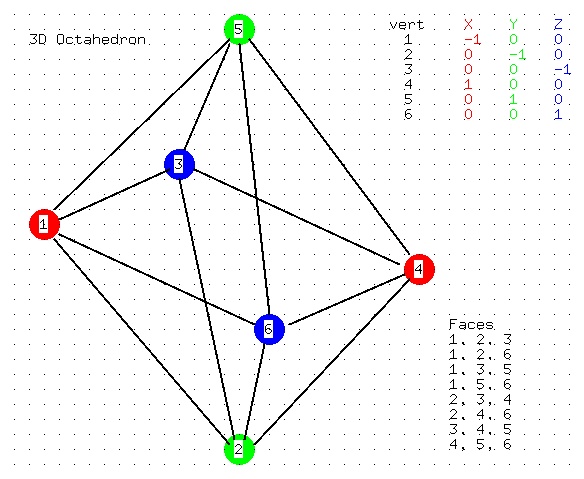
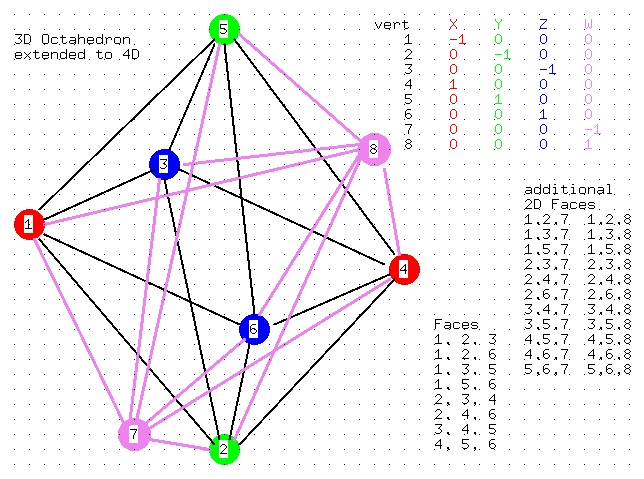

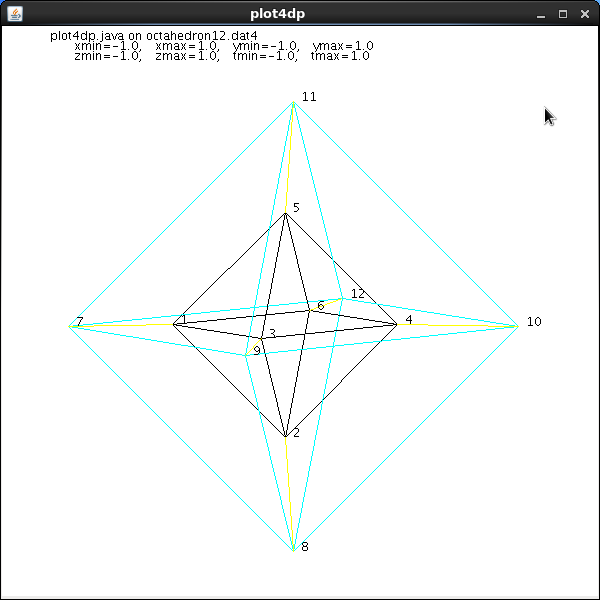 Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
faces.c running, data for various n-cubes, n dimensions
0-cube point
vertices = 1
1-cube line
edges = 1
vertices = 2
2-cube square
2D faces = 1
edges = 4
vertices = 4
3-cube cube
cubes = 1
2D faces = 6
edges = 12
vertices = 8
n=4-cube
4-cubes = 1
cubes = 8
2D faces = 24
edges = 32
vertices = 16
D-1 surface D volume
2D circle 2 Pi R Pi R^2
3D sphere 4 Pi R^2 4/3 Pi R^3
4D 4-sphere 2 Pi^2 R^3 1/2 Pi^2 R^4
one definition of sequence of n-spheres
for n=8
a1, a2, a3, a4, a5, a6, a7 are angles, typ: theta, phi, ...
x1, x2, x3, x4, x5, x6, x7, x8 are orthogonal coordinates
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 + x6^2 + x7^2 +x8^2 = R^2
Radius R = sqrt(R^2)
2D circle
x1 = R sin(a1) typ: y theta
x2 = R cos(a1) typ: x theta
a1 = arctan(x1/x2)
3D sphere
x1 = R sin(a2) sin(a1) typ: y phi theta
x2 = R sin(a2) cos(a1) typ: x phi theta
x3 = R cos(a2) typ: z phi
a1 = arctan(sqrt(x1^2+x2^2)/x3)
a2 = arctan(x1/x2)
4D 4-sphere
x1 = R sin(a3) sin(a2) sin(a1) typ: y
x2 = R sin(a3) sin(a2) cos(a1) typ: x
x3 = R sin(a3) cos(a2) typ: z
x4 = R cos(a3) typ: w
a1 = arctan(sqrt(x1^2+x2^2+x3^2)/x4)
a2 = arctan(sqrt(x1^2+x2^2)/x3)
a3 = arctan(x1/x2)
If you have not seen it yet:
flatland clip
www.flatlandthemovie.com
Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
faces.c running, data for various n-cubes, n dimensions
0-cube point
vertices = 1
1-cube line
edges = 1
vertices = 2
2-cube square
2D faces = 1
edges = 4
vertices = 4
3-cube cube
cubes = 1
2D faces = 6
edges = 12
vertices = 8
n=4-cube
4-cubes = 1
cubes = 8
2D faces = 24
edges = 32
vertices = 16
D-1 surface D volume
2D circle 2 Pi R Pi R^2
3D sphere 4 Pi R^2 4/3 Pi R^3
4D 4-sphere 2 Pi^2 R^3 1/2 Pi^2 R^4
one definition of sequence of n-spheres
for n=8
a1, a2, a3, a4, a5, a6, a7 are angles, typ: theta, phi, ...
x1, x2, x3, x4, x5, x6, x7, x8 are orthogonal coordinates
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 + x6^2 + x7^2 +x8^2 = R^2
Radius R = sqrt(R^2)
2D circle
x1 = R sin(a1) typ: y theta
x2 = R cos(a1) typ: x theta
a1 = arctan(x1/x2)
3D sphere
x1 = R sin(a2) sin(a1) typ: y phi theta
x2 = R sin(a2) cos(a1) typ: x phi theta
x3 = R cos(a2) typ: z phi
a1 = arctan(sqrt(x1^2+x2^2)/x3)
a2 = arctan(x1/x2)
4D 4-sphere
x1 = R sin(a3) sin(a2) sin(a1) typ: y
x2 = R sin(a3) sin(a2) cos(a1) typ: x
x3 = R sin(a3) cos(a2) typ: z
x4 = R cos(a3) typ: w
a1 = arctan(sqrt(x1^2+x2^2+x3^2)/x4)
a2 = arctan(sqrt(x1^2+x2^2)/x3)
a3 = arctan(x1/x2)
If you have not seen it yet:
flatland clip
www.flatlandthemovie.com
<- previous index next ->
Many web sites on Java GUI, AWT, Swing, etc.
Many web sites on Python wx, tk, qt, etc.
 Notation: x is left and right.
y is up and down
z is forward and back
w is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
Notation: x is left and right.
y is up and down
z is forward and back
w is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
 Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, w
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, w
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
 4th dimension smaller
4th dimension smaller
 source code plot4d_gl.c
plot4d data generator f4d.c
source code plot4d_gl.c
plot4d data generator f4d.c

 Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.
Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.



 Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
faces.c running, data for various n-cubes, n dimensions
0-cube point
vertices = 1
1-cube line
edges = 1
vertices = 2
2-cube square
2D faces = 1
edges = 4
vertices = 4
3-cube cube
cubes = 1
2D faces = 6
edges = 12
vertices = 8
n=4-cube
4-cubes = 1
cubes = 8
2D faces = 24
edges = 32
vertices = 16
D-1 surface D volume
2D circle 2 Pi R Pi R^2
3D sphere 4 Pi R^2 4/3 Pi R^3
4D 4-sphere 2 Pi^2 R^3 1/2 Pi^2 R^4
one definition of sequence of n-spheres
for n=8
a1, a2, a3, a4, a5, a6, a7 are angles, typ: theta, phi, ...
x1, x2, x3, x4, x5, x6, x7, x8 are orthogonal coordinates
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 + x6^2 + x7^2 +x8^2 = R^2
Radius R = sqrt(R^2)
2D circle
x1 = R sin(a1) typ: y theta
x2 = R cos(a1) typ: x theta
a1 = arctan(x1/x2)
3D sphere
x1 = R sin(a2) sin(a1) typ: y phi theta
x2 = R sin(a2) cos(a1) typ: x phi theta
x3 = R cos(a2) typ: z phi
a1 = arctan(sqrt(x1^2+x2^2)/x3)
a2 = arctan(x1/x2)
4D 4-sphere
x1 = R sin(a3) sin(a2) sin(a1) typ: y
x2 = R sin(a3) sin(a2) cos(a1) typ: x
x3 = R sin(a3) cos(a2) typ: z
x4 = R cos(a3) typ: w
a1 = arctan(sqrt(x1^2+x2^2+x3^2)/x4)
a2 = arctan(sqrt(x1^2+x2^2)/x3)
a3 = arctan(x1/x2)
If you have not seen it yet:
flatland clip
www.flatlandthemovie.com
Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
faces.c running, data for various n-cubes, n dimensions
0-cube point
vertices = 1
1-cube line
edges = 1
vertices = 2
2-cube square
2D faces = 1
edges = 4
vertices = 4
3-cube cube
cubes = 1
2D faces = 6
edges = 12
vertices = 8
n=4-cube
4-cubes = 1
cubes = 8
2D faces = 24
edges = 32
vertices = 16
D-1 surface D volume
2D circle 2 Pi R Pi R^2
3D sphere 4 Pi R^2 4/3 Pi R^3
4D 4-sphere 2 Pi^2 R^3 1/2 Pi^2 R^4
one definition of sequence of n-spheres
for n=8
a1, a2, a3, a4, a5, a6, a7 are angles, typ: theta, phi, ...
x1, x2, x3, x4, x5, x6, x7, x8 are orthogonal coordinates
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 + x6^2 + x7^2 +x8^2 = R^2
Radius R = sqrt(R^2)
2D circle
x1 = R sin(a1) typ: y theta
x2 = R cos(a1) typ: x theta
a1 = arctan(x1/x2)
3D sphere
x1 = R sin(a2) sin(a1) typ: y phi theta
x2 = R sin(a2) cos(a1) typ: x phi theta
x3 = R cos(a2) typ: z phi
a1 = arctan(sqrt(x1^2+x2^2)/x3)
a2 = arctan(x1/x2)
4D 4-sphere
x1 = R sin(a3) sin(a2) sin(a1) typ: y
x2 = R sin(a3) sin(a2) cos(a1) typ: x
x3 = R sin(a3) cos(a2) typ: z
x4 = R cos(a3) typ: w
a1 = arctan(sqrt(x1^2+x2^2+x3^2)/x4)
a2 = arctan(sqrt(x1^2+x2^2)/x3)
a3 = arctan(x1/x2)
If you have not seen it yet:
flatland clip
www.flatlandthemovie.com