<- previous index next ->
To start, perspective Viewing, Resize Choices and Transformation Matrices.
This lecture reviews the technical details and mathematics that
makes a 2D screen look like a 3D scene.
We then move do displaying 4D, 5D and 6D on a 2D screen.
Think matematics, not physics, 4, 5 or 6 independent variables
with one dependent value are 4D, 5D, 6D.
In the simplest case, computing the i,j screen position of
a vertex at world coordinates x,y,z is accomplished by
multiplying a 4 by 4 perspective matrix by a 4 by 4 model matrix
times the x,y,z,w vertex vector, then placing the i,j in
the viewport.
 Shows the frustum that contains the 3D "World" that is to be
presented to the user. Any objects with more positive Z than "near"
are clipped, any objects with more negative values of Z than "far"
are clipped. Any objects outside of the X or Y of the frustum
are clipped. The positive Z axis is considered to come
out of the screen toward the viewer.
Name the vertices on the diagram as:
On the 'near' rectangle, the lower left is 'xmin' 'ymin'
the upper left is 'xmin' 'ymax'
the lower right is 'xmax' 'ymin'
the upper right is 'xmax' 'ymax'
The distance from the eye to near is 'near' a positive number
The distance from the eye to far is 'far' a positive number
The 4 by 4 perspective matrix is
|2*near/(xmax-xmin) 0.0 (xmax+xmin)/(xmax-xmin) 0.0 |
| |
| 0.0 2*near/(ymax-ymin) (ymax+ymin)/(ymax-ymin) 0.0 |
| |
| 0.0 0.0 -(far+near)/(far-near) -2*far*near/(far-near)|
| |
| 0.0 0.0 -1.0 0.0 |
The OpenGL call to create this perspective matrix is:
glFrustum(xmin, xmax, ymin, ymax, near, far);
An alternate call uses the vertical the eye position, looking at
the center of interest, + on 'far', and Y up=1, X up=0, Z up=0 is:
gluLookAt(eyex, eyey, eyez, coix, coiy, coiz, Xup, Yup, Zup);
Yet another alternative using the angle, field of view, and
w/h aspect ratio is:
gluPerspective(angle, w/h, near, far);
The model view matrix begins as the identity matrix and is multiplied
by the users rotations, scaling and translations. The world coordinates
may be in any system of physical units, yet all coordinates must
be in the same units. The six degrees of freedom for a solid 3D object
are to to translate in three dimensions and rotate about three axis.
The translation matrix to translate 0,0,0 to x,y,z is
| 1.0 0.0 0.0 x |
| 0.0 1.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 z |
| 0.0 0.0 0.0 1.0 |
glTranslatef(x, y, z);
The scaling matrix to scale x by sx, y by sy and z by sz is
| sx 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 |
| 0.0 0.0 0.0 1.0 |
glScalef(sx, sy, sz);
The rotation matrix by angle a about the X axis is
| 1.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 |
| 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 1.0, 0.0, 0.0);
The rotation matrix by angle a about the Y axis is
| cos a 0.0 sin a 0.0 |
| 0.0 1.0 0.0 0.0 |
| -sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 1.0, 0.0);
The rotation matrix by angle a about the Z axis is
| cos a -sin a 0.0 0.0 |
| sin a cos a 0.0 0.0 |
| 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 0.0, 1.0);
A user world coordinate vertex p = x, y, z, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.z)-xmin)/(xmax-xmin)
screen y = h * ((pp.y/pp.z)-ymin)/(ymax-ymin)
Trying to check that the equations are correct,
the program demo_mat.c writes out OpenGL matrices.
The output is demo_mat.out
The equations are coded in check_mat.c
The output is check_mat.out
It seems that OpenGL stores the matrix column major (Fortran style)
while the "C" program stores the matrix row major, causing the
printout to appear to be the transpose.
Row Major, first row first: C, Java, Python
{[0][0], [0][1], [0][2], [1][0], [1][1], [1][2], [2][0], [2][1], [2][2]}
Column Major, first column first: Fortran, Matlab
((1,1),(2,1),(3,1), (1,2),(2,2),(3,2), (1,3),(2,3),(3,3))
The same geometry and same data were used in both programs.
The final result from both is essentially the same.
output from demo_mat.c OpenGL
0.5, 1.5, 2.5 at win x=25.798641, y=345.927915, z=0.827098
output from check_mat.c
x scr, y scr=25.798841, 345.927778 at relative z=0.827098)
width, height =300.000000, 400.000000
In OpenGL or equivalently in your code, you can save the present matrix
and start with a new identity matrix, do transformations, cause actions,
then revert back the the prior matrix.
glPushMatrix();
glLoadIdentity();
glRotatef(theta[0], 1.0, 0.0, 0.0);
glRotatef(theta[1], 0.0, 1.0, 0.0);
glRotatef(theta[2], 0.0, 0.0, 1.0);
glTranslatef(pos[0], pos[1], pos[2]);
/* use the Model view matrix to do something */
glPopMatrix();
/* a possible Reshape, it happens on first expose and every change */
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(w <= h) /* e.g size = 2.0, x in -2.0 .. 2.0 */
glOrtho(-size, size, /* xmin, xmax */
-size*(GLfloat)h/(GLfloat)w, size*(GLfloat)h/(GLfloat)w,
/* ymin, ymax */
-10.0, 10.0); /* near in real Z value, far as real Z value */
else
glOrtho(-size*(GLfloat)w/(GLfloat)h, size*(GLfloat)w/(GLfloat)h,
-size, size, /* Y is size, w/h for X */
-10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
/* go do Display or something */
Shows the frustum that contains the 3D "World" that is to be
presented to the user. Any objects with more positive Z than "near"
are clipped, any objects with more negative values of Z than "far"
are clipped. Any objects outside of the X or Y of the frustum
are clipped. The positive Z axis is considered to come
out of the screen toward the viewer.
Name the vertices on the diagram as:
On the 'near' rectangle, the lower left is 'xmin' 'ymin'
the upper left is 'xmin' 'ymax'
the lower right is 'xmax' 'ymin'
the upper right is 'xmax' 'ymax'
The distance from the eye to near is 'near' a positive number
The distance from the eye to far is 'far' a positive number
The 4 by 4 perspective matrix is
|2*near/(xmax-xmin) 0.0 (xmax+xmin)/(xmax-xmin) 0.0 |
| |
| 0.0 2*near/(ymax-ymin) (ymax+ymin)/(ymax-ymin) 0.0 |
| |
| 0.0 0.0 -(far+near)/(far-near) -2*far*near/(far-near)|
| |
| 0.0 0.0 -1.0 0.0 |
The OpenGL call to create this perspective matrix is:
glFrustum(xmin, xmax, ymin, ymax, near, far);
An alternate call uses the vertical the eye position, looking at
the center of interest, + on 'far', and Y up=1, X up=0, Z up=0 is:
gluLookAt(eyex, eyey, eyez, coix, coiy, coiz, Xup, Yup, Zup);
Yet another alternative using the angle, field of view, and
w/h aspect ratio is:
gluPerspective(angle, w/h, near, far);
The model view matrix begins as the identity matrix and is multiplied
by the users rotations, scaling and translations. The world coordinates
may be in any system of physical units, yet all coordinates must
be in the same units. The six degrees of freedom for a solid 3D object
are to to translate in three dimensions and rotate about three axis.
The translation matrix to translate 0,0,0 to x,y,z is
| 1.0 0.0 0.0 x |
| 0.0 1.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 z |
| 0.0 0.0 0.0 1.0 |
glTranslatef(x, y, z);
The scaling matrix to scale x by sx, y by sy and z by sz is
| sx 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 |
| 0.0 0.0 0.0 1.0 |
glScalef(sx, sy, sz);
The rotation matrix by angle a about the X axis is
| 1.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 |
| 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 1.0, 0.0, 0.0);
The rotation matrix by angle a about the Y axis is
| cos a 0.0 sin a 0.0 |
| 0.0 1.0 0.0 0.0 |
| -sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 1.0, 0.0);
The rotation matrix by angle a about the Z axis is
| cos a -sin a 0.0 0.0 |
| sin a cos a 0.0 0.0 |
| 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 0.0, 1.0);
A user world coordinate vertex p = x, y, z, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.z)-xmin)/(xmax-xmin)
screen y = h * ((pp.y/pp.z)-ymin)/(ymax-ymin)
Trying to check that the equations are correct,
the program demo_mat.c writes out OpenGL matrices.
The output is demo_mat.out
The equations are coded in check_mat.c
The output is check_mat.out
It seems that OpenGL stores the matrix column major (Fortran style)
while the "C" program stores the matrix row major, causing the
printout to appear to be the transpose.
Row Major, first row first: C, Java, Python
{[0][0], [0][1], [0][2], [1][0], [1][1], [1][2], [2][0], [2][1], [2][2]}
Column Major, first column first: Fortran, Matlab
((1,1),(2,1),(3,1), (1,2),(2,2),(3,2), (1,3),(2,3),(3,3))
The same geometry and same data were used in both programs.
The final result from both is essentially the same.
output from demo_mat.c OpenGL
0.5, 1.5, 2.5 at win x=25.798641, y=345.927915, z=0.827098
output from check_mat.c
x scr, y scr=25.798841, 345.927778 at relative z=0.827098)
width, height =300.000000, 400.000000
In OpenGL or equivalently in your code, you can save the present matrix
and start with a new identity matrix, do transformations, cause actions,
then revert back the the prior matrix.
glPushMatrix();
glLoadIdentity();
glRotatef(theta[0], 1.0, 0.0, 0.0);
glRotatef(theta[1], 0.0, 1.0, 0.0);
glRotatef(theta[2], 0.0, 0.0, 1.0);
glTranslatef(pos[0], pos[1], pos[2]);
/* use the Model view matrix to do something */
glPopMatrix();
/* a possible Reshape, it happens on first expose and every change */
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(w <= h) /* e.g size = 2.0, x in -2.0 .. 2.0 */
glOrtho(-size, size, /* xmin, xmax */
-size*(GLfloat)h/(GLfloat)w, size*(GLfloat)h/(GLfloat)w,
/* ymin, ymax */
-10.0, 10.0); /* near in real Z value, far as real Z value */
else
glOrtho(-size*(GLfloat)w/(GLfloat)h, size*(GLfloat)w/(GLfloat)h,
-size, size, /* Y is size, w/h for X */
-10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
/* go do Display or something */
 The simplest equations for orthographic projection are given by:
Xs, Ys are 2D screen coordinates. Assume 0,0 at lower left.
X,Y,Z are 3D world coordinates. Assume 0,0,0 at lower left.
Xs = X + cos(theta)*Z
Ys = Y + sin(theta)*Z
Scaling and offsets may be provided as required.
Theta is the angle up from the Xp axis to the where the 3D Z axis is drawn
Doing your own 3D projection may be easiest as orthographic.
For example, in this simple 3D shape entry program, the entry is
in XY (front view), XZ (top view), or YZ (side view) plane then
shown in three views and as orthographic.
The source is draw3D3.java
with output:
The simplest equations for orthographic projection are given by:
Xs, Ys are 2D screen coordinates. Assume 0,0 at lower left.
X,Y,Z are 3D world coordinates. Assume 0,0,0 at lower left.
Xs = X + cos(theta)*Z
Ys = Y + sin(theta)*Z
Scaling and offsets may be provided as required.
Theta is the angle up from the Xp axis to the where the 3D Z axis is drawn
Doing your own 3D projection may be easiest as orthographic.
For example, in this simple 3D shape entry program, the entry is
in XY (front view), XZ (top view), or YZ (side view) plane then
shown in three views and as orthographic.
The source is draw3D3.java
with output:
 A first cut at 4D, four dimensional rendering, uses 5 by 5 matrices:
Note that there are now eight (8) degrees of freedom:
Move in X, Y, Z, T and rotations about each axis (split into 6 matrices)
A first cut at 4D, four dimensional rendering, uses 5 by 5 matrices:
Note that there are now eight (8) degrees of freedom:
Move in X, Y, Z, T and rotations about each axis (split into 6 matrices)
 Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
 Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, t
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, t
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
4D sphere
 4th dimension smaller
4th dimension smaller
User control for plotting any two of x, y, z, t
against the value of function u(x,y,z,t)
source code plot_4d.java
 source code plot4d_gl.c
plot4d data generator f4d.c
source code plot4d_gl.c
plot4d data generator f4d.c
 Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.
Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.
octrahedron in 3D and increased to 4D

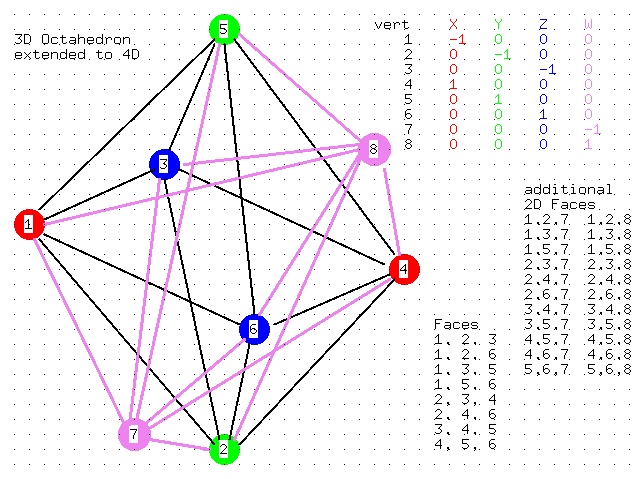

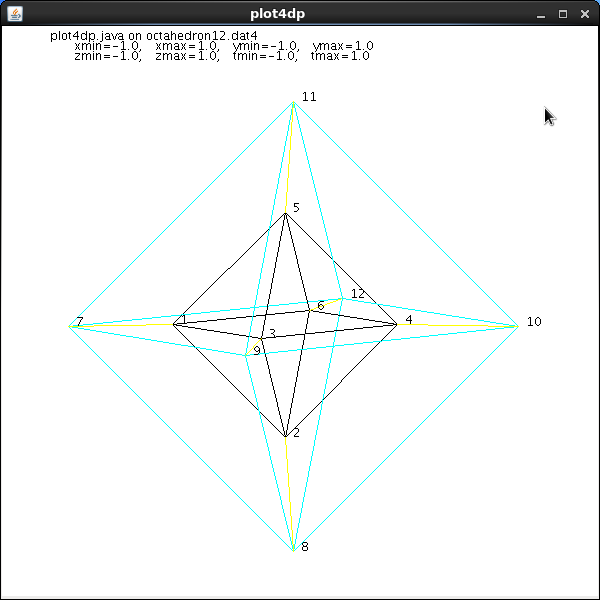 Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
Of course, this extends to 5D and 6D and 7D
source code plot5d_gl.c
source code plot6d_gl.c
source code plot7d_gl.c
source code plot5d.java
source code plot6d.java
source code plot7d.java
Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
Of course, this extends to 5D and 6D and 7D
source code plot5d_gl.c
source code plot6d_gl.c
source code plot7d_gl.c
source code plot5d.java
source code plot6d.java
source code plot7d.java

Some 5D data
5D cube data cube.dat5
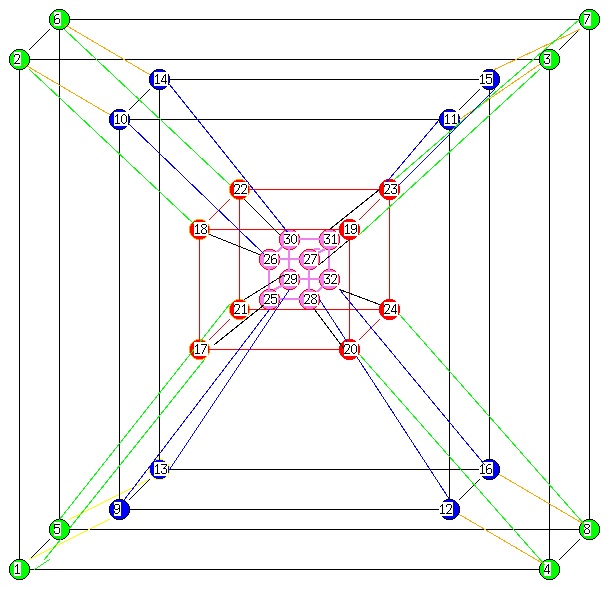
Cube and Sphere to higher dimensions
faces.c source
faces.out shown below
faces.c running, data for various n-cubes, n dimensions
0-cube point
vertices = 1
1-cube line
edges = 1
vertices = 2
2-cube square
2D faces = 1
edges = 4
vertices = 4
3-cube cube
cubes = 1
2D faces = 6
edges = 12
vertices = 8
n=4-cube
4-cubes = 1
cubes = 8
2D faces = 24
edges = 32
vertices = 16
n=5-cube
5-cubes = 1
4-cubes = 10
cubes = 40
2D faces = 80
edges = 80
vertices = 32
n=6-cube
6-cubes = 1
5-cubes = 12
4-cubes = 60
cubes = 160
2D faces = 240
edges = 192
vertices = 64
n=7-cube
7-cubes = 1
6-cubes = 14
5-cubes = 84
4-cubes = 280
cubes = 560
2D faces = 672
edges = 448
vertices = 128
n=8-cube
8-cubes = 1
7-cubes = 16
6-cubes = 112
5-cubes = 448
4-cubes = 1120
cubes = 1792
2D faces = 1792
edges = 1024
vertices = 256
D-1 surface D volume
2D circle 2 Pi R Pi R^2
3D sphere 4 Pi R^2 4/3 Pi R^3
4D 4-sphere 2 Pi^2 R^3 1/2 Pi^2 R^4
5D 5-sphere 8/3 Pi^2 R^4 8/15 Pi^2 R^5
6D 6-sphere Pi^3 R^5 1/6 Pi^3 R^6
7D 7-sphere 16/15 Pi^3 R^6 16/105 Pi^3 R^7
8D 8-sphere 1/3 Pi^4 R^7 1/24 Pi^4 R^8
9D 9-sphere 32/105 Pi^4 R^8 32/945 Pi^4 R^9
volume V_n(R)= Pi^(n/2) R^n / gamma(n/2+1)
gamma(integer) = factorial(integer-1) gamma(5) = 24
gamma(1/2) = sqrt(Pi), gamma(n/2+1) = (2n)! sqrt(Pi)/(4^n n!)
or V_2k(R) = Pi^k R^2k/k! , V_2k+1 = 2 k! (4Pi)^k R^(2k+1)/(2k+1)!
surface area A_n(R) = d/dR V_n(R)
10D 10-sphere volume 1/120 Pi^5 R^10
10D 10-sphere area 1/12 Pi^5 R^9
one definition of sequence of n-spheres
for n=8
a1, a2, a3, a4, a5, a6, a7 are angles, typ: theta, phi, ...
x1, x2, x3, x4, x5, x6, x7, x8 are orthogonal coordinates
x1^2 + x2^2 + x3^2 + x4^2 + x5^2 + x6^2 + x7^2 +x8^2 = R^2
Radius R = sqrt(R^2)
2D circle
x1 = R sin(a1) typ: y theta
x2 = R cos(a1) typ: x theta
a1 = arctan(x1/x2)
3D sphere
x1 = R sin(a2) sin(a1) typ: y phi theta
x2 = R sin(a2) cos(a1) typ: x phi theta
x3 = R cos(a2) typ: z phi
a1 = arctan(sqrt(x1^2+x2^2)/x3)
a2 = arctan(x1/x2)
4D 4-sphere
x1 = R sin(a3) sin(a2) sin(a1)
x2 = R sin(a3) sin(a2) cos(a1)
x3 = R sin(a3) cos(a2)
x4 = R cos(a3)
a1 = arctan(sqrt(x1^2+x2^2+x3^2)/x4)
a2 = arctan(sqrt(x1^2+x2^2)/x3)
a3 = arctan(x1/x2)
5D 5-sphere
x1 = R sin(a4) sin(a3) sin(a2) sin(a1)
x2 = R sin(a4) sin(a3) sin(a2) cos(a1)
x3 = R sin(a4) sin(a3) cos(a2)
x4 = R sin(a4) cos(a3)
x5 = R cos(a4)
6D 6-sphere
x1 = R sin(a5) sin(a4) sin(a3) sin(a2) sin(a1)
x2 = R sin(a5) sin(a4) sin(a3) sin(a2) cos(a1)
x3 = R sin(a5) sin(a4) sin(a3) cos(a2)
x4 = R sin(a5) sin(a4) cos(a3)
x5 = R sin(a5) cos(a4)
x6 = R cos(a5)
7D 7-sphere
x1 = R sin(a6) sin(a5) sin(a4) sin(a3) sin(a2) sin(a1)
x2 = R sin(a6) sin(a5) sin(a4) sin(a3) sin(a2) cos(a1)
x3 = R sin(a6) sin(a5) sin(a4) sin(a3) cos(a2)
x4 = R sin(a6) sin(a5) sin(a4) cos(a3)
x5 = R sin(a6) sin(a5) cos(a4)
x6 = R sin(a6) cos(a5)
x7 = R cos(a6)
8D 8-sphere
x1 = R sin(a7) sin(a6) sin(a5) sin(a4) sin(a3) sin(a2) sin(a1)
x2 = R sin(a7) sin(a6) sin(a5) sin(a4) sin(a3) sin(a2) cos(a1)
x3 = R sin(a7) sin(a6) sin(a5) sin(a4) sin(a3) cos(a2)
x4 = R sin(a7) sin(a6) sin(a5) sin(a4) cos(a3)
x5 = R sin(a7) sin(a6) sin(a5) cos(a4)
x6 = R sin(a7) sin(a6) cos(a5)
x7 = R sin(a7) cos(a6)
x8 = R cos(a7)
faces.c finished
If you have not seen it yet:
flatland clip
www.flatlandthemovie.com
<- previous index next ->
Many web sites on Java GUI, AWT, Swing, etc.
Many web sites on Python wx, tk, qt, etc.
 Shows the frustum that contains the 3D "World" that is to be
presented to the user. Any objects with more positive Z than "near"
are clipped, any objects with more negative values of Z than "far"
are clipped. Any objects outside of the X or Y of the frustum
are clipped. The positive Z axis is considered to come
out of the screen toward the viewer.
Name the vertices on the diagram as:
On the 'near' rectangle, the lower left is 'xmin' 'ymin'
the upper left is 'xmin' 'ymax'
the lower right is 'xmax' 'ymin'
the upper right is 'xmax' 'ymax'
The distance from the eye to near is 'near' a positive number
The distance from the eye to far is 'far' a positive number
The 4 by 4 perspective matrix is
|2*near/(xmax-xmin) 0.0 (xmax+xmin)/(xmax-xmin) 0.0 |
| |
| 0.0 2*near/(ymax-ymin) (ymax+ymin)/(ymax-ymin) 0.0 |
| |
| 0.0 0.0 -(far+near)/(far-near) -2*far*near/(far-near)|
| |
| 0.0 0.0 -1.0 0.0 |
The OpenGL call to create this perspective matrix is:
glFrustum(xmin, xmax, ymin, ymax, near, far);
An alternate call uses the vertical the eye position, looking at
the center of interest, + on 'far', and Y up=1, X up=0, Z up=0 is:
gluLookAt(eyex, eyey, eyez, coix, coiy, coiz, Xup, Yup, Zup);
Yet another alternative using the angle, field of view, and
w/h aspect ratio is:
gluPerspective(angle, w/h, near, far);
The model view matrix begins as the identity matrix and is multiplied
by the users rotations, scaling and translations. The world coordinates
may be in any system of physical units, yet all coordinates must
be in the same units. The six degrees of freedom for a solid 3D object
are to to translate in three dimensions and rotate about three axis.
The translation matrix to translate 0,0,0 to x,y,z is
| 1.0 0.0 0.0 x |
| 0.0 1.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 z |
| 0.0 0.0 0.0 1.0 |
glTranslatef(x, y, z);
The scaling matrix to scale x by sx, y by sy and z by sz is
| sx 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 |
| 0.0 0.0 0.0 1.0 |
glScalef(sx, sy, sz);
The rotation matrix by angle a about the X axis is
| 1.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 |
| 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 1.0, 0.0, 0.0);
The rotation matrix by angle a about the Y axis is
| cos a 0.0 sin a 0.0 |
| 0.0 1.0 0.0 0.0 |
| -sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 1.0, 0.0);
The rotation matrix by angle a about the Z axis is
| cos a -sin a 0.0 0.0 |
| sin a cos a 0.0 0.0 |
| 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 0.0, 1.0);
A user world coordinate vertex p = x, y, z, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.z)-xmin)/(xmax-xmin)
screen y = h * ((pp.y/pp.z)-ymin)/(ymax-ymin)
Trying to check that the equations are correct,
the program demo_mat.c writes out OpenGL matrices.
The output is demo_mat.out
The equations are coded in check_mat.c
The output is check_mat.out
It seems that OpenGL stores the matrix column major (Fortran style)
while the "C" program stores the matrix row major, causing the
printout to appear to be the transpose.
Row Major, first row first: C, Java, Python
{[0][0], [0][1], [0][2], [1][0], [1][1], [1][2], [2][0], [2][1], [2][2]}
Column Major, first column first: Fortran, Matlab
((1,1),(2,1),(3,1), (1,2),(2,2),(3,2), (1,3),(2,3),(3,3))
The same geometry and same data were used in both programs.
The final result from both is essentially the same.
output from demo_mat.c OpenGL
0.5, 1.5, 2.5 at win x=25.798641, y=345.927915, z=0.827098
output from check_mat.c
x scr, y scr=25.798841, 345.927778 at relative z=0.827098)
width, height =300.000000, 400.000000
In OpenGL or equivalently in your code, you can save the present matrix
and start with a new identity matrix, do transformations, cause actions,
then revert back the the prior matrix.
glPushMatrix();
glLoadIdentity();
glRotatef(theta[0], 1.0, 0.0, 0.0);
glRotatef(theta[1], 0.0, 1.0, 0.0);
glRotatef(theta[2], 0.0, 0.0, 1.0);
glTranslatef(pos[0], pos[1], pos[2]);
/* use the Model view matrix to do something */
glPopMatrix();
/* a possible Reshape, it happens on first expose and every change */
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(w <= h) /* e.g size = 2.0, x in -2.0 .. 2.0 */
glOrtho(-size, size, /* xmin, xmax */
-size*(GLfloat)h/(GLfloat)w, size*(GLfloat)h/(GLfloat)w,
/* ymin, ymax */
-10.0, 10.0); /* near in real Z value, far as real Z value */
else
glOrtho(-size*(GLfloat)w/(GLfloat)h, size*(GLfloat)w/(GLfloat)h,
-size, size, /* Y is size, w/h for X */
-10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
/* go do Display or something */
Shows the frustum that contains the 3D "World" that is to be
presented to the user. Any objects with more positive Z than "near"
are clipped, any objects with more negative values of Z than "far"
are clipped. Any objects outside of the X or Y of the frustum
are clipped. The positive Z axis is considered to come
out of the screen toward the viewer.
Name the vertices on the diagram as:
On the 'near' rectangle, the lower left is 'xmin' 'ymin'
the upper left is 'xmin' 'ymax'
the lower right is 'xmax' 'ymin'
the upper right is 'xmax' 'ymax'
The distance from the eye to near is 'near' a positive number
The distance from the eye to far is 'far' a positive number
The 4 by 4 perspective matrix is
|2*near/(xmax-xmin) 0.0 (xmax+xmin)/(xmax-xmin) 0.0 |
| |
| 0.0 2*near/(ymax-ymin) (ymax+ymin)/(ymax-ymin) 0.0 |
| |
| 0.0 0.0 -(far+near)/(far-near) -2*far*near/(far-near)|
| |
| 0.0 0.0 -1.0 0.0 |
The OpenGL call to create this perspective matrix is:
glFrustum(xmin, xmax, ymin, ymax, near, far);
An alternate call uses the vertical the eye position, looking at
the center of interest, + on 'far', and Y up=1, X up=0, Z up=0 is:
gluLookAt(eyex, eyey, eyez, coix, coiy, coiz, Xup, Yup, Zup);
Yet another alternative using the angle, field of view, and
w/h aspect ratio is:
gluPerspective(angle, w/h, near, far);
The model view matrix begins as the identity matrix and is multiplied
by the users rotations, scaling and translations. The world coordinates
may be in any system of physical units, yet all coordinates must
be in the same units. The six degrees of freedom for a solid 3D object
are to to translate in three dimensions and rotate about three axis.
The translation matrix to translate 0,0,0 to x,y,z is
| 1.0 0.0 0.0 x |
| 0.0 1.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 z |
| 0.0 0.0 0.0 1.0 |
glTranslatef(x, y, z);
The scaling matrix to scale x by sx, y by sy and z by sz is
| sx 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 |
| 0.0 0.0 0.0 1.0 |
glScalef(sx, sy, sz);
The rotation matrix by angle a about the X axis is
| 1.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 |
| 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 1.0, 0.0, 0.0);
The rotation matrix by angle a about the Y axis is
| cos a 0.0 sin a 0.0 |
| 0.0 1.0 0.0 0.0 |
| -sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 1.0, 0.0);
The rotation matrix by angle a about the Z axis is
| cos a -sin a 0.0 0.0 |
| sin a cos a 0.0 0.0 |
| 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 1.0 |
glRotatef(a, 0.0, 0.0, 1.0);
A user world coordinate vertex p = x, y, z, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.z)-xmin)/(xmax-xmin)
screen y = h * ((pp.y/pp.z)-ymin)/(ymax-ymin)
Trying to check that the equations are correct,
the program demo_mat.c writes out OpenGL matrices.
The output is demo_mat.out
The equations are coded in check_mat.c
The output is check_mat.out
It seems that OpenGL stores the matrix column major (Fortran style)
while the "C" program stores the matrix row major, causing the
printout to appear to be the transpose.
Row Major, first row first: C, Java, Python
{[0][0], [0][1], [0][2], [1][0], [1][1], [1][2], [2][0], [2][1], [2][2]}
Column Major, first column first: Fortran, Matlab
((1,1),(2,1),(3,1), (1,2),(2,2),(3,2), (1,3),(2,3),(3,3))
The same geometry and same data were used in both programs.
The final result from both is essentially the same.
output from demo_mat.c OpenGL
0.5, 1.5, 2.5 at win x=25.798641, y=345.927915, z=0.827098
output from check_mat.c
x scr, y scr=25.798841, 345.927778 at relative z=0.827098)
width, height =300.000000, 400.000000
In OpenGL or equivalently in your code, you can save the present matrix
and start with a new identity matrix, do transformations, cause actions,
then revert back the the prior matrix.
glPushMatrix();
glLoadIdentity();
glRotatef(theta[0], 1.0, 0.0, 0.0);
glRotatef(theta[1], 0.0, 1.0, 0.0);
glRotatef(theta[2], 0.0, 0.0, 1.0);
glTranslatef(pos[0], pos[1], pos[2]);
/* use the Model view matrix to do something */
glPopMatrix();
/* a possible Reshape, it happens on first expose and every change */
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(w <= h) /* e.g size = 2.0, x in -2.0 .. 2.0 */
glOrtho(-size, size, /* xmin, xmax */
-size*(GLfloat)h/(GLfloat)w, size*(GLfloat)h/(GLfloat)w,
/* ymin, ymax */
-10.0, 10.0); /* near in real Z value, far as real Z value */
else
glOrtho(-size*(GLfloat)w/(GLfloat)h, size*(GLfloat)w/(GLfloat)h,
-size, size, /* Y is size, w/h for X */
-10.0, 10.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
/* go do Display or something */
 The simplest equations for orthographic projection are given by:
Xs, Ys are 2D screen coordinates. Assume 0,0 at lower left.
X,Y,Z are 3D world coordinates. Assume 0,0,0 at lower left.
Xs = X + cos(theta)*Z
Ys = Y + sin(theta)*Z
Scaling and offsets may be provided as required.
Theta is the angle up from the Xp axis to the where the 3D Z axis is drawn
Doing your own 3D projection may be easiest as orthographic.
For example, in this simple 3D shape entry program, the entry is
in XY (front view), XZ (top view), or YZ (side view) plane then
shown in three views and as orthographic.
The source is draw3D3.java
with output:
The simplest equations for orthographic projection are given by:
Xs, Ys are 2D screen coordinates. Assume 0,0 at lower left.
X,Y,Z are 3D world coordinates. Assume 0,0,0 at lower left.
Xs = X + cos(theta)*Z
Ys = Y + sin(theta)*Z
Scaling and offsets may be provided as required.
Theta is the angle up from the Xp axis to the where the 3D Z axis is drawn
Doing your own 3D projection may be easiest as orthographic.
For example, in this simple 3D shape entry program, the entry is
in XY (front view), XZ (top view), or YZ (side view) plane then
shown in three views and as orthographic.
The source is draw3D3.java
with output:
 A first cut at 4D, four dimensional rendering, uses 5 by 5 matrices:
Note that there are now eight (8) degrees of freedom:
Move in X, Y, Z, T and rotations about each axis (split into 6 matrices)
A first cut at 4D, four dimensional rendering, uses 5 by 5 matrices:
Note that there are now eight (8) degrees of freedom:
Move in X, Y, Z, T and rotations about each axis (split into 6 matrices)
 Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
The 8 "3D faces" are:
1 2 3 4 5 6 7 8 inside
1 2 3 4 9 10 11 12 front
1 2 6 5 9 10 14 13 left
1 4 8 5 9 12 16 13 bottom
2 3 7 6 10 11 15 14 top
3 4 7 8 11 12 16 15 right
5 6 7 8 13 14 15 16 back
9 10 11 12 13 14 15 16 outside
as a check, every vertex must appear on exactly 8 faces.
There are 24 "2D faces" shown in cube.dat4
cube.dat4 unit hypercube data
The 5 by 5 perspective matrix is
|2*near 0.0 0.0 xmax+xmin 0.0 |
|--------- --------- |
|xmax-xmin xmax-xmin |
| |
| 0.0 2*near 0.0 ymax+ymin 0.0 |
| -------- --------- |
| ymax-ymin ymax-ymin |
| |
| 0.0 0.0 2*near zmax+zmin 0.0 |
| ------- ----------- |
| zmax-zmin zmax-zmin |
| |
| 0.0 0.0 0.0 -(far+near) -2*far*near |
| ----------- ----------- |
| far-near far-near |
| |
| 0.0 0.0 0.0 -1.0 0.0 |
The model view matrix is the product of the needed matrices below.
The translation matrix to translate 0,0,0,0 to x,y,z,t is
| 1.0 0.0 0.0 0.0 x |
| 0.0 1.0 0.0 0.0 y | unused translations are 0.0
| 0.0 0.0 1.0 0.0 z |
| 0.0 0.0 0.0 1.0 t |
| 0.0 0.0 0.0 0.0 1.0 |
translate(x, y, z, t)
The scaling matrix to scale x by sx, y by sy, z by sz, t by st is
| sx 0.0 0.0 0.0 0.0 |
| 0.0 sy 0.0 0.0 0.0 | unused scales are 1.0
| 0.0 0.0 sz 0.0 0.0 |
| 0.0 0.0 0.0 st 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
scale(sx, sy, sz, st)
The six rotation matrices are combined to make the four rotations:
The rotation matrix by angle a about the X,T axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a -sin a 0.0 0.0 |
| 0.0 sin a cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 0.0, 1.0)
The rotation matrix by angle a about the Y,T axis is
| cos a 0.0 -sin a 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| sin a 0.0 cos a 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 0.0, 1.0)
The rotation matrix by angle a about the Z,T axis is
| cos a -sin a 0.0 0.0 0.0 |
| sin a cos a 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 0.0 0.0 1.0 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 0.0, 1.0, 1.0)
The rotation matrix by angle a about the X,Y axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 cos a -sin a 0.0 |
| 0.0 0.0 sin a cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 1.0, 0.0, 0.0)
The rotation matrix by angle a about the X,Z axis is
| 1.0 0.0 0.0 0.0 0.0 |
| 0.0 cos a 0.0 -sin a 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| 0.0 sin a 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 1.0, 0.0, 1.0, 0.0)
The rotation matrix by angle a about the Y,Z axis is
| cos a 0.0 0.0 -sin a 0.0 |
| 0.0 1.0 0.0 0.0 0.0 |
| 0.0 0.0 1.0 0.0 0.0 |
| sin a 0.0 0.0 cos a 0.0 |
| 0.0 0.0 0.0 0.0 1.0 |
rotate(a, 0.0, 1.0, 1.0, 0.0)
To get a rotation about only the X axis,
use the matrix product of X,Y X,Z X,T
To get a rotation about only the Y axis,
use the matrix product of X,Y Y,Z Y,T
To get a rotation about only the Z axis,
use the matrix product of X,Z Y,Z Z,T
To get a rotation about only the T axis,
use the matrix product of X,T Y,T Z,T
A user world coordinate vertex p = x, y, z, t, w (w=1.0)
is transformed into pp by
perspective matrix times model view matrix times p is pp
To get screen coordinates, given the screen width w, and
screen height h,
screen x = w * ((pp.x/pp.t)-xmin)/(xmax-xmin) ?
screen y = h * ((pp.y/pp.t)-ymin)/(ymax-ymin) ?
 Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, t
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
Notation: x is left and right.
y is up and down
z is forward and back
t is in and out (a fourth spacial dimension)
Vertices x, y, z, t
1 0, 0, 0, 0
2 1, 0, 0, 0
3 1, 1, 0, 0
4 1, 1, 1, 0
5 0, 0, 0, 1
6 1, 0, 0, 1
7 1, 1, 0, 1
8 1, 1, 1, 1
as a check, every vertex must appear on exactly 6 faces.
There are 14 "2D faces" shown in tetra.dat4
tetra.dat4 unit 4D Tetrahedron data
This is possible, yet really difficult, another approach is
to use a dynamic display and allow the user to select
the independent variables to be changed.
 4th dimension smaller
4th dimension smaller
 source code plot4d_gl.c
plot4d data generator f4d.c
source code plot4d_gl.c
plot4d data generator f4d.c
 Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.
Front and side display can be any pair.
The right side shows the other two variables.
Step for looking at individual values,
"run" for moving display.



 Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
Of course, this extends to 5D and 6D and 7D
source code plot5d_gl.c
source code plot6d_gl.c
source code plot7d_gl.c
source code plot5d.java
source code plot6d.java
source code plot7d.java
Data file for light_dat3
octahedron3.dat
Data file for plot4dp (java)
octahedron4.dat4
Data file for plot4dp (java)
octahedron12.dat4
source code plot4dp.java
Of course, this extends to 5D and 6D and 7D
source code plot5d_gl.c
source code plot6d_gl.c
source code plot7d_gl.c
source code plot5d.java
source code plot6d.java
source code plot7d.java

