MATH 481, Project 4: Population Models
Due Thursday April 18
Malthus' model
Verhulst's model
Verhulst's model with quota harvesting
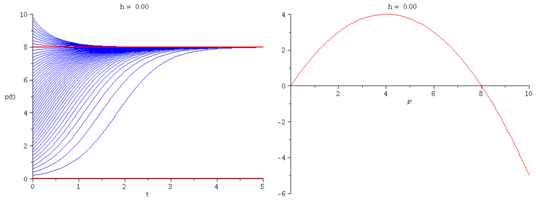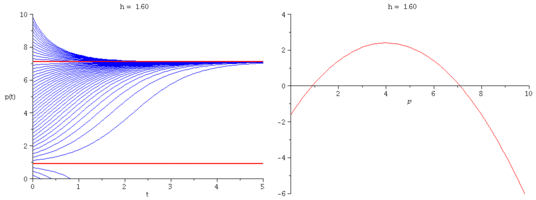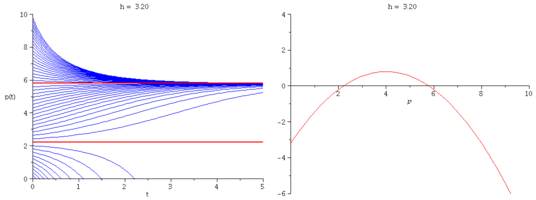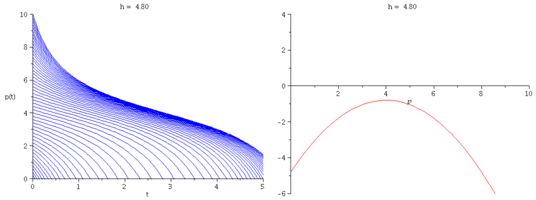
We modify Verhulst's model by introducing a constant harvesting rate $h$:
\[
\frac{dp}{dt} = r\Big(1-\frac{p}{k}\Big)p - h.
\]
- What is the critical harvesting value $h_c$ so that
the population has no chance of survival when $h > h_c$?
Express $h_c$ in terms of $r$ and $k$.
- Plot representative solution curves for several values of $h$.
- This animation can give you ideas for your article:
The predator-prey model
- Explain the derivation of the predator-prey model
\begin{align*}
\frac{dx}{dt} &= ( a_1 - b_{11} x - b_{12} y)x, \\
\frac{dy}{dt} &= (-a_2 + b_{21} x - b_{22} y)y.
\end{align*}
- Describe the essential features of the system's
phase portrait and its equilibria. Qualitatively,
there are two distinct cases, depending on whether
$a_1/b_{11} < a_2/b_{21}$ or $a_1/b_{11} > a_2/b_{21}$.
Show a sample phase portrait for each case.
- Introduce harvesting proportional to the population of
each species. If the system has a nontrivial equilibrium
(i.e., an equilibrium where both populations are positive),
how does harvesting affect it? This relates to Volterra's
explanation of the increase of the fraction of selachians in
the fish caught in the Adriatic Sea during the WWI.
The Lotka and Volterra exchange
Reference:
An extract from Martin Braun's book
Vito Volterra published a summary of his analysis of
the surge in the fraction of the Adriatic selachian population in the
October 16, 1926 issue of Nature. The full account was published in a 1927 report titled
Variazioni e Fluttuazioni del numero d'individui in specie animali conviventi.
In a Letter to the Editor in the
January 1, 1927, Alfred Lotka pointed out that
the October article duplicates parts of the analysis in his book
that was published in Baltimore in 1925.
Volterra responded in
the same issue, acknowledging Lotka's remark, and wrote:
“In this I recognize his priority,
and am sorry not to have known his work,
and therefore not to have been able to mention it.”
Their predator-prey
model is now known as the Lotka–Volterra model,
although most commonly the model is presented without the overcrowding
effects, that is, with $b_{11} = b_{22} = 0$.


