Skew Heaps
A skew heap is a type of heap data structure that, like a standard max-heap, has efficient insert(), max(), and removeMax() operations, but also allows for efficient merging of heaps. Unlike a standard heap, it is not space-efficient to implement a skew heap in an array or vector &ldash; we will have to use a linked binary tree structure.
Your skew heap must satisfy the Max-heap Property, which you were introduced to in Project 3: for any node \(w\) in the tree, the priority of \(w\) must be greater than the priorities of its two children. This property guarantees that the element with highest priority is always in the root node of the tree, and so reading the highest priority element is just a matter of accessing the data in the root node.
The special feature of a skew heap is the merge operation which combines two skew heaps into a single, valid skew heap. Let p1 and p2 be positions in two skew heaps (e.g. pointers to nodes). Further, suppose the methods left() and right() return positions of the left and right children, and priority() returns the priority of a position. The merge operation is defined recursively:
The following figure shows two skew heaps (blue and green) and the result of merging the two. All the steps of the merge procedure are described below the figure.
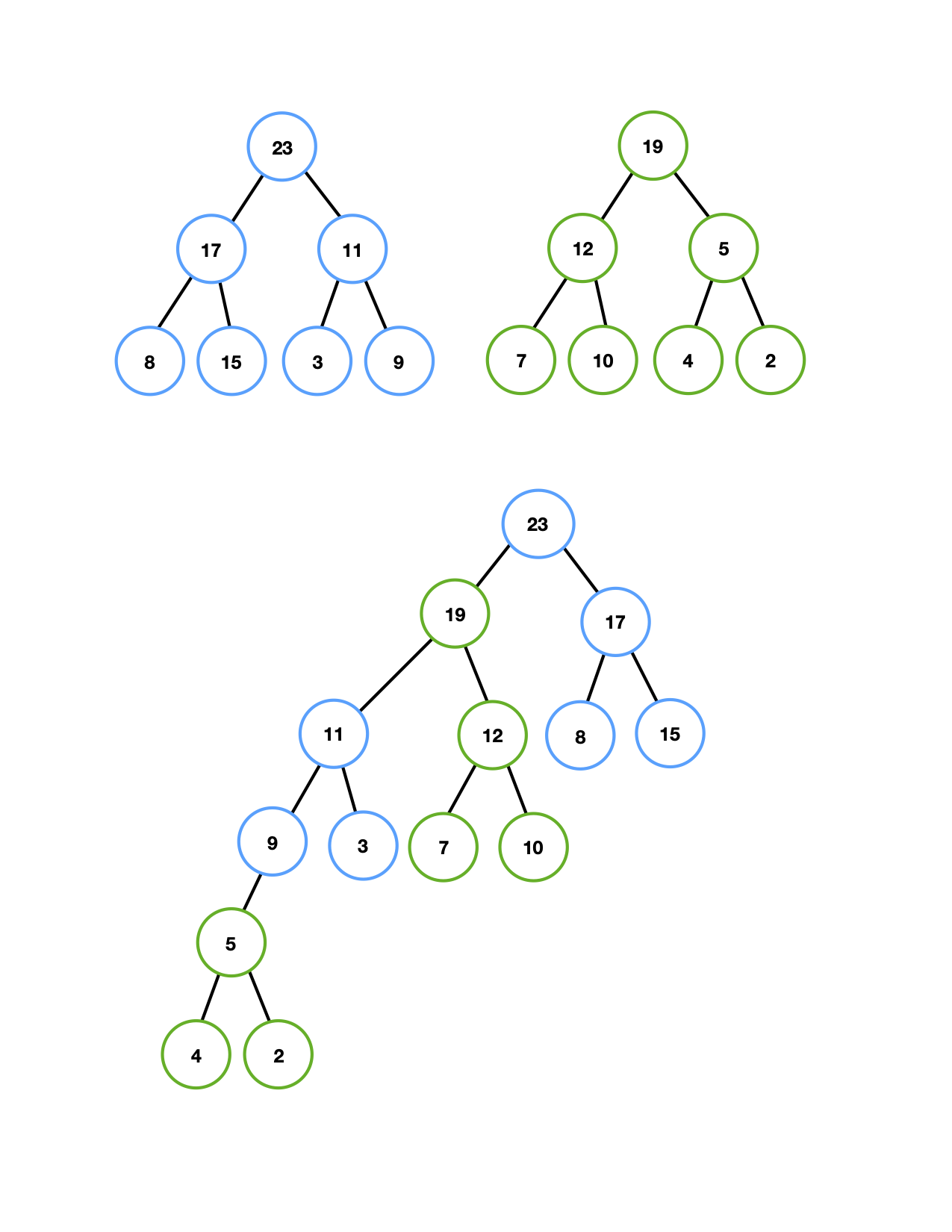
-
First Merge
- Make (23) the new root since 23 > 19.
- Swap (23)'s left and right subtrees.
- Recursively Merge (23)'s left subtree, which is the blue subtree rooted at (11), with the other skew heap; replace (23)'s left subtree with the merged subtree.
-
Second Merge
Merge the green heap with the blue subtree rooted at (11).- Make (19) the root since 19 > 11.
- Swap (19)'s left and right subtrees.
- Recursively Merge (19)'s left subtree (rooted at (5)) with the subtree rooted at (11); replace (19)'s left subtree with the merged tree.
-
Third Merge
Merge the green subtree rooted at (5) with the blue subtree rooted at (11).- Make (11) the root since 11 > 5.
- Swap (11)'s left and right subtrees.
- Recursively Merge (11)'s left subtree (the single node (9)) with the green subtree rooted at (5); replace (11)'s left subtree with the merged tree.
-
Fourth Merge
Merge the green subtree rooted at (5) with the single node (9).- Make (9) the root sinc 9 > 5.
- (9) has no children, so we don't have to swap anything.
- Recursively Merge (9)'s left subtree (which is empty!) with the green subtree rooted at (5); replace (9)'s left subtree with the merged tree.
-
Fifth Merge
This is a trivial merge since one of the two trees is empty. We simply return the non-empty tree, which in this case is the green subtree rooted at (5).
Other Operations
The major operations supported by a max-skew heap are insertion of elements, reading the highest priority element, and removing the highest priority element. Reading the highest priority element is just a matter of reading the root node of the heap. The other two operations, insertion and removal, are applications of the merge function:
- To insert a new node x into an exiting skew heap H, we treat x as a single-node skew heap and merge it with H.
- To remove the maximum priority value, we delete the root node and then merge the root's left and right sub-heaps.
We see, then, that the merge function is key to all of the major skew heap operations. If we can implement merge correctly, insertion and removal are simple.