Project 3: Treaps
Due: Tuesday, November 5, before 9:00 pm
Addenda
- The original version of treap.h included my declarations of private helper functions, some of which are not relevant to the project. It has been corrected. The original version is still available and has been renamed treap_old.h.
- The original version of treap.h was missing #include <limits>. It has been corrected.
Objectives
The objectives of this programming assignment are:
- Practice constructing and using binary search trees.
- Practice writing basic rebalancing routines (single rotations).
Introduction
A treap is a combination of a binary search tree (BST) and a heap. You should be very familiar with BSTs at this point in the semester, but you probably haven't encountered heaps yet. For this project, you only need two concepts from heaps:
- Each node of the tree, in addition to holding a data value, will also store an integer priority value. Priority values should be unique; that is, no two nodes should have the same priority.
- The tree must have the Max-Heap Property: for any node \(w\) in the tree, the priority of \(w\) must be greater than the priorities of its two children.
The following figure shows a treap in which the data are letters (or strings) and the priorities are integers.
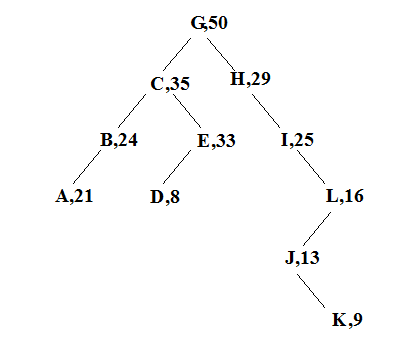
(Image source: http://cseweb.ucsd.edu/~kube/cls/100/Lectures/lec5/lec5-2.html#pgfId-955731)
A treap must be both a BST and have the max-heap property, which means insertions and deletions must check that the max-heap property holds and fix the tree if it does not. It will turn out that this is not as bad as it sounds. The max-heap property can always be repaired by applying single rotations.
Tree Rotations
Single tree rotations are local modification to a tree that can be used to repair violations of the max-heap property while maintaining the BST structure. The restructurings that can be achieved using single rotations are a subset of those possible with trinode restructuring. The figure below illustrates left and right single rotations.
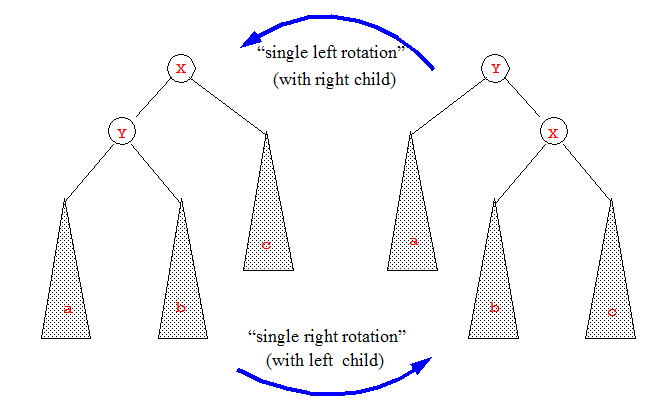
(Image source: http://cseweb.ucsd.edu/~kube/cls/100/Lectures/lec5/lec5-5.html#pgfId-955859)
It is not difficult to see that rotations preserve the BST ordering: in both images, we have \(a < Y < b < X < c\), and we assume that the subtrees \(a\), \(b\), and \(c\) were constructed correctly before the rotation occured. How dow we use rotations to make local fixes to the max-heap property? Suppose that in the left picture, the priority of \(Y\) were higher than the priority of \(X\), violating the max-heap property; then a right rotation would make \(Y\) the parent of \(X\), correcting the error.
We can use single rotations, along with standard BST operations, to maintain a treap.
-
Insertion: suppose we have a value-priority pair \((v, p)\) that we wish to insert into a treap. Assume that \(p\) is unique. We first perform a normal BST insertion, which creates a new leaf node. Then, if \(p\) is greater than the priority of the parent, we do a left or right single roation to move \((v, p)\) up in the tree.
Now \((v,p)\) will have a new parent, and it is possible that \(p\) is still larger than the new parent's priority, in which case we perform another rotation; repeat, moving \((v,p)\) up the tree, until the max-heap property is satisfied at each node.
-
Deletion: suppose we wish to remove the node with value \(v\). We begin with a normal BST search to see if \(v\) is in fact in the tree; if not, do nothing.
If we find \(v\) and it is a leaf node, we can simply delete the node. If it is not a leaf node, perform a sequence of left and right rotations to move \(v\) down the tree until it is a leaf, and then delete it. When performing the rotations, you should choose the direction (left or right) that moves the child with largest priority higher in the tree.
So why bother with treaps? One interesting fact is that if we build a treap using random priorities it will almost always be balanced (meaning, balanced with high probability); at the same time, treaps are easier to implement than balanced trees such as AVL or red-black trees. Also, there are other operations that can be performed efficiently on treaps, such as joining two treaps to create a single combined treap, or splitting a treap into two treaps.
A good reference for additional information is this lecture on treaps from UCSD.
Assignment
Your assignment is to implement the Treap class using single rotation method described in the Introduction to maintain the treap properties. You must use the provided treap.h and treap.cpp files. You may not modify the public function declarations or private data, but you may add private helper functions.
Although several test programs are provided, you are responsible for thoroughly testing your program. It is particularly important that your code run without segmentation faults, memory leaks, or memory errors. Memory leaks are considered as bad as segmentation fault since many segmentation faults are caused by poorly written destructors. A program with a poorly written destructor might avoid some segmentation faults but will leak memory horribly. Memory leaks will incur a penalty similar to that of a segmentation fault.
Following is a alist of member functions that must be implemented. Some of these functions are already implemented (or partially implemented) in treap.cpp; others will need to be written from scratch. Any helper functions that you write must be private and must be declared in treap.h.
-
A default constructor with the signature:
Treap::Treap() ;
Note: An implementation of this methods is provided in treap.cpp.
The default constructor must create a Treap object that is ready for treap operations such insertion, removal, search, and inorder traversal. Even an empty tree should behave properly when its methods are called.
-
A copy constructor with the signature:
Treap::Treap(const Treap& other) ;
The copy constructor must make a deep copy and create a new object that has its own allocated memory.
-
A destructor with the signature:
Treap::~Treap() ;
The destructor must completely free all memory allocated for the object. (Use valgrind on GL to check for memory leaks.)
-
An overloaded assignment operator with the signature:
const Treap& Treap::operator=(const Treap& rhs) ;
The assignment operator must deallocate memory used by the host object and then make deep copy of rhs.
-
A function that deterimes if the treap is empty having the following signature:
bool Treap::empty() const;
Note: An implementation of this methods is provided in treap.cpp.
The empty() function should return true if the tree is empty and false otherwise.
-
A function that returns the height of the tree. It should have the following signature:
int Treap::height() const;
Note: An implementation of this methods is provided in treap.cpp.
The height() function should return the height of the tree. The height is stored in the TreapNode pointed to by the treap object and must be maintained by the node insertion and removal methods.
-
A function that returns the priority of the node. The priority function should should have the signature:
priority_t Treap::priority() const;
Note: An implementation of this methods is provided in treap.cpp.
The priority() function should return the priority stored in the TreapNode object.
-
An insertion function that adds a data-priority pair to Treap and has the following signature:
void Treap::insert( data_t data, priority_t pri ) ;
The insert() function must maintain the treap properties (BST with max-heap property) and run in time proportional to the height of the treap. Your implementation must not allow duplicate data values. If the insert() function is invoked with a data value that already stored in the Treap, your insert() function should do nothing.
-
A treap removal function that finds and removes an item with the given data value. The remove() function should return a boolean value that indicates whether the data value was found; it should not abort or throw an exception when the key is not stored in the BST. The remove() member function must have the following signature:
bool Treap::remove(data_t data) ;
For full credit, your remove() method must run in time proportional to the height of the tree.
-
A find function that reports whether the given data value is stored in the tree. The signature of the find() method must be:
const data_t* Treap::find(const data_t& x) ;
If the data value x is found, find() returns a pointer to the corresponding data value; otherwise it returns nullptr. Your find() method must run in time proportional to the height of the tree.
-
A member function inorder() that performs an inorder traversal and prints the data in a specified format. It must have the following signature:
void Treap::inorder() ;
Note: An implementation of this methods is provided in treap.cpp.
The inorder() methods visits each node using an inorder traversal, prints out the data, followed by a :, followed by the priority, then another :, and then the height of the node. It also prints an open parenthesis before visiting the left subtree and a close parenthesis after visiting the right subtree. Nothing is printed when inorder() is called on an empty tree, not even parentheses. This function will be used for grading and is useful for debugging.
For example, calling inorder() on the sample treap from the introduction should produce the string:
((((A:21:0)B:24:1)C:35:2((D:8:0)E:33:1))G:50:5(H:29:4(I:25:3((J:13:1(K:9:0))L:16:2))))

Sample Treap with String Data and Integer Priorities
(Image source: http://cseweb.ucsd.edu/~kube/cls/100/Lectures/lec5/lec5-2.html#pgfId-955731)Here, the G:50:5 indicates that the node with data “G” and priority 50 has height 5. The output before G:50:5 is produced by visiting the left subtree, and everything after G:50:5 is produced by visiting the right subtree.
-
A function locate() that returns whether there is a node in a particular position of the Treap and stores the data, priority, and height in reference parameters. The function must have the signature:
bool Treap::locate(const char position[], data_t& x, priority_t& p, int& h, int offset=0) ;
Note: An implementation of this methods is provided in treap.cpp.
The position is given by a constant C-string, where a character L indicates left and a character R indicates right.
For example in the treap above:
- A call to locate("LRL", data) should return true and store D in data.
- A call to locate("RRRL", data) should return true and store J in data.
-
A call to locate("RLR", data) should return
false and not make any changes to data
since there is no node in that
position.
Note: locate() must not abort and must not throw an exception in this situation. - A call to locate("", data) should return true and store G in data, since the empty string indicates the root of tree.
The grading programs will use locate() to check if your treap is correct.
-
A dump function that prints information about all the nodes in the tree. The function must have the signature:
void Treap::dump() ;
Note: An implementation of this methods is provided in treap.cpp.
Sample output from the dump() called on the sample treap is provided in dump_sample.txt.
Additional Requirements
Requirement: You must use the supplied treap.h and treap.cpp files. You may not modify any of the public method prototypes or private data, although you may add private functions.
Requirement: Your find(), insert() and remove() methods must all run in time proportional to the height of the treap.
Requirement: Your implementation must not permit duplicate data values. If an attempt is made to insert a duplicate value, insert() should leave the treap unchanged; it should not throw an exception or cause the program to crash.
Requirement: The treap properties must hold after any call to insert() or remove(). These commands must produce a valid treap.
Requirement: Your code must use single rotations as described in the Introduction to maintain the treap properties.
Requirement: Except for insert(), the provided function implementations should not be modified.
Provided Programs
The provided class files, treap.h and treap.cpp, comprise a partial implementation of a BST, providing a constructor, insert() function, and inorder() traversal, and it is possible to create and print a BST with no additional code. The following driver is provided:
- driver.cpp — simple driver for the basic BST implementation.
Several sample test programs for the Treap class are provided below. However, it is your responsibility to write additional tests to ensure that your implementation is correct.
-
Builds the treap from the
Introduction.
test0.cpp
Sample output: test0.txt -
Builds the treap from the Introduction and
then deletes “K” and “C”.
test1.cpp
Sample outptu: test1.txt -
Test of the copy constructor.
test2.cpp
Sample output: test2.txt -
Test of the assignment operator.
test3.cpp
Sample output: test3.txt -
Test of the locate() function.
test4.cpp
Sample output: test4.txt
What to Submit
You must submit the following files to the proj3 directory.
- treap.h
- treap.cpp
If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.