<- previous index next ->
Some mathematical techniques have multiple uses in graphics.
The understanding of the development may be more important
than a specific chunk of code because your specific need may
be slightly different.
In order to not loose everyone in notation, we start with one
dimension, then we wave our hands and say it now should be obvious
in three dimensions. :)
Our goal is to do interesting manipulations of 3D patches.
The smallest useful patch is 16 3D points forming a 4 by 4 mesh.
Starting easy, consider four values of x, e.g. x0, x1, x2, x3
that can also be represented as a vector X.
Given that the x's are evenly spaced, we want to find an easy and
efficient way to compute intermediate values. This is called
interpolation.
The solution is to create a polynomial, P(u), with an independent
variable u that goes from 0.0 to 1.0 such that:
P(0) = x0
P(1/3) = x1
P(2/3) = x2
P(1) = x3
and any value of u between 0.0 and 1.0 gives a reasonable value for x.
(Note the equal spacing, 0 to 1/3, 1/3 to 2/3, 2/3 to 1)
There are various approximations that can be used if we do not need
exact equality at every point. For example, see the GUI tutorial on
spline fit. For the purpose of understanding, we use the exact fit by
a third order polynomial.
P(u) = c0 + c1*u + c2*u^2 + c3*u^3
A side note is that we use Horner's rule for the actual computation
P(u) = c0 +u*(c1 + u*(c2 + u*c3))
using three multiplications and three additions.
In vector notation, C represents the four values c0, c1, c2, c3.
Now, combining what we have so far, e.g. p(1/3) = x1 and P(u), in a
neat form we can see the matrix-vector version of our problem.
P(0) = c0 + c1*(0) + c2*(0)^2 + c3*(0)^3 = x0
P(1/3) = c0 + c1*(1/3) + c2*(1/3)^2 + c3*(1/3)^3 = x1
P(2/3) = c0 + c1*(2/3) + c2*(2/3)^2 + c3*(2/3)^3 = x2
P(1) = c0 + c1*(1) + c2*(1)^2 + c3*(1)^3 = x3
Noting that this is a set of simultaneous equations,
define the constant matrix A from the equations above
| 1 0 0 0 |
A = | 1 1/3 1/9 1/27 |
| 1 2/3 4/9 8/27 |
| 1 1 1 1 |
and writing the matrix vector equation (ignoring row vs column vectors)
C * A = X
We know the values of X and A, thus we directly compute C using
C = A^(-1) * X
compute the inverse of matrix A and multiply by vector X to get vector C.
For computational efficiency, the inverse of A is computed at most once
and can be used for many different X vectors. Having the C vector,
Horner's method is used to compute the intermediate values at the
u needed by our graphics application.
simeq.c Solves simultaneous equations and computes inverse.
Now for the hand waving. Using the method described above and considering
a 3D point having x,y and z, we can compute three C vectors, Cx, Cy and Cz
by using X, Y, and Z vectors, thus getting three polynomials
Px(u), Py(u) and Pz(u) that interpolate and produce an x, y and z for
each value of u in the range 0.0 to 1.0. 'u' is known as the parameter
and the equations are called parametric equations for x, y, z.
What is usually needed is interpolation in two dimensions, say u and v,
for a two dimensional mesh of three dimensional points. Thus we have
16 points and this would need 16 c's for an exact fit, needing
16 by 16 matrices. In order to get better computational speed, smoothing
is applied and Bezier or cubic B-Splines are typically used.
To really get deep into surface patches, check out Non Uniform Rational
B-Splines, NURBS.
The use of "patches" allows complex surfaces to be drawn with a few
pixels when far away and many pixels when close up. Thus uniformly
good quality images may be displayed with only as many computations
as are needed.
For example, bteapot.c displays the wireframe.
bteapot uses vertices.h
teapot.c has the data internal, and has a
bug in the data that creates a crack in the pot. Cracked pot?
Modeling techniques.
Suppose you want to model characters that are going to move and perform
actions. In 2D the character would be drawn by the creative artist in
a number of situations. An author would create the story line. An
animator would draw the character at various stages in the story.
Other people would fill in the frames between the stages. Other people
would "ink and paint" the frames so that every 1/24 of a second a
frame could be displayed and the viewer would see smooth natural
motion as the character went about doing the story line. This is
still being performed and computers are helping some, but it is still
a lot of work.
In 3D modeling such as the movies Toy Story and Finding Nemo the
effort is even greater. Typically each frame must exists in terms
of geometry of objects, texture mapping, coloring, materials and
lighting. Out takes of many animations have been shown. One from
Shrek presented a dress moving one way and the princess moving
the other way, oops, the texture mapping coordinates were wrong.
In movies such as Madagascar and Over The Hedge there was a
line of code for every hair in some closeups.
Thus additional math is needed and more is being used. Once the
character is modeled in 3D, the motion can be computed for
actions such as walking and running. Once the motion is computable
then all the joint movements can be computed. Some of the motion
is captured by placing "dots" on human subjects and recording the
position and angle of body parts. Using human motions can make the
characters more "life like", more pleasing to the eye.
Complex figures, such as The Incredibles and Robots, seem to be using
a technique where the body is modeled by limbs as lines, then
ellipsoids are placed on the limbs. The actual appearance of skin is
computed based on an elastic mesh that covers the ellipsoids.
Not quite the exact physics of skin because the tension on the
mesh has to be adjusted on various parts of the body. Actions
such as taking a punch in the stomach are computed by deformation
of the mesh.
The creative talent of artists, authors and animators
is still needed. Much of the other work may be assisted by
mathematical computations.
over the hedge trailer
UMBC Game Club:
gain.umbc.edu
Or, record massive amounts of data, such as Internet traffic
over 24 hours over the globe and present a time moving display.
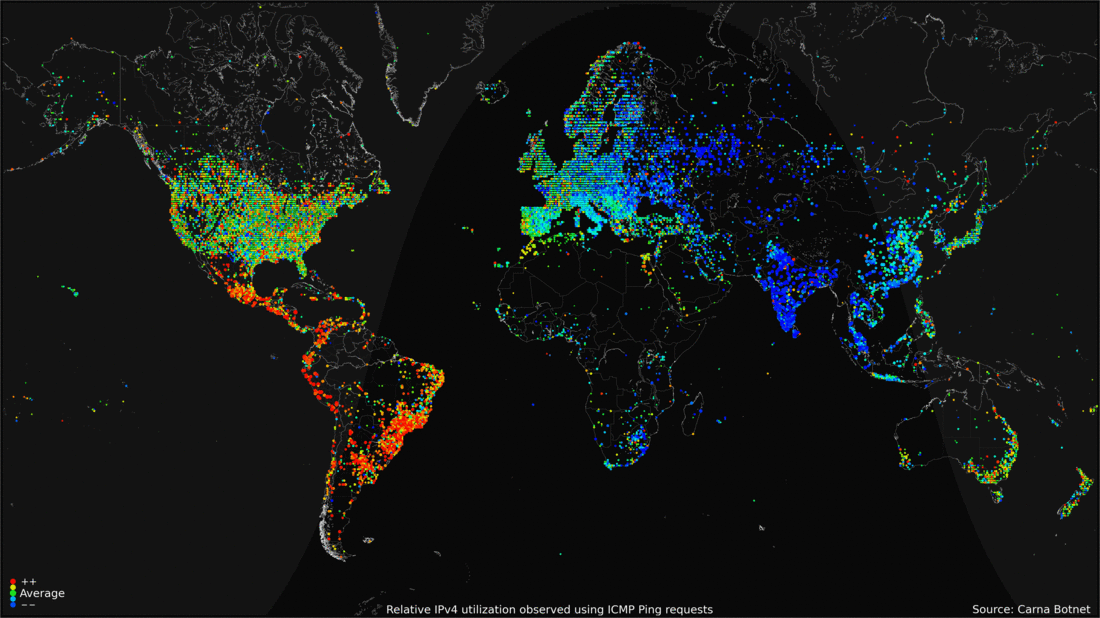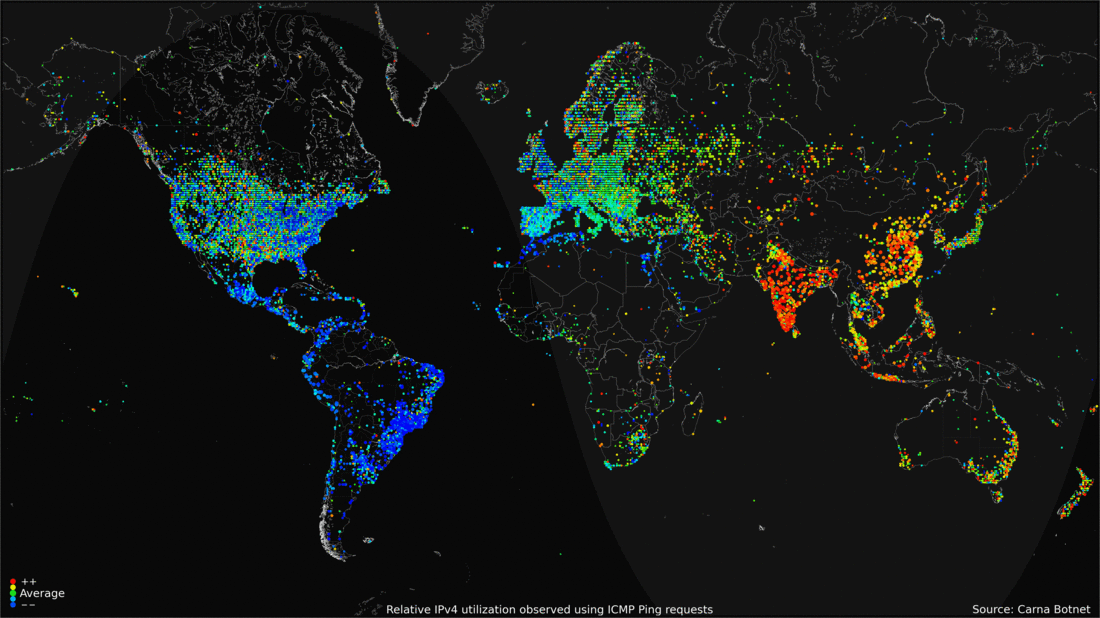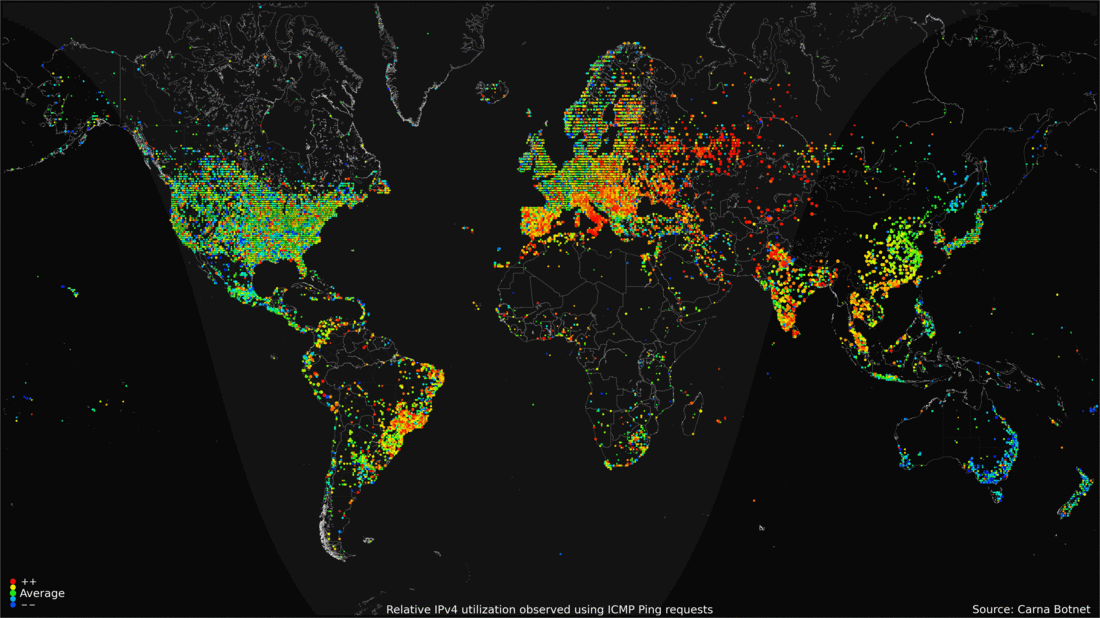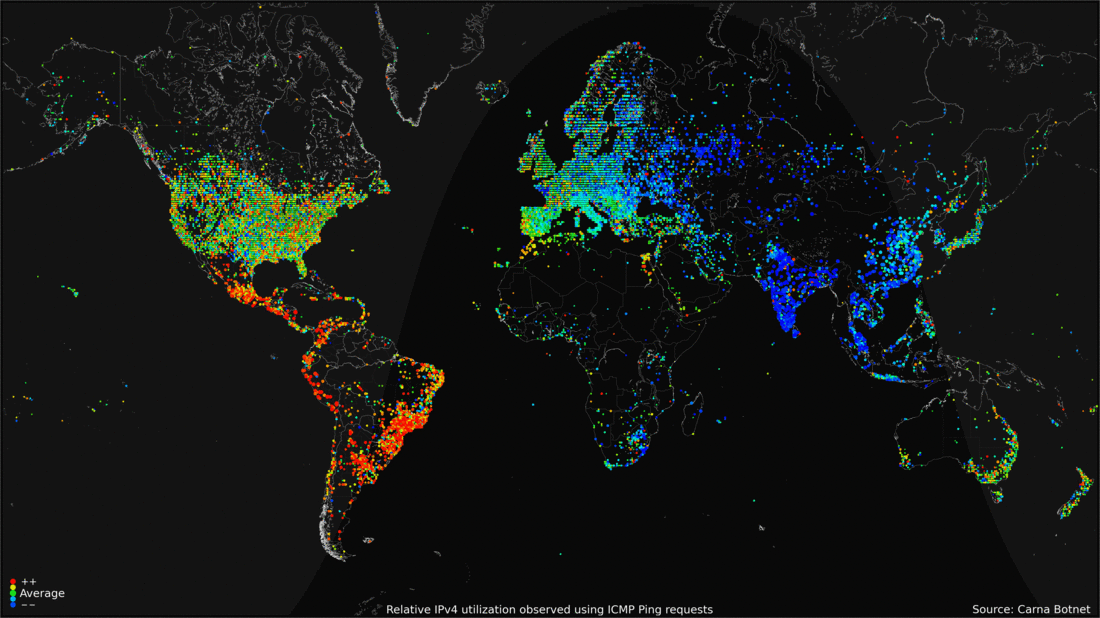
<- previous index next ->
Many web sites on Java GUI, AWT, Swing, etc.
Many web sites on Python wx, tk, qt, etc.

