<- previous index next ->
"Pan" means move the viewport left, right, up, or down. The image
stays in the same place in world coordinates.
"Zoom" in or out by moving the viewer closer to, or farther from the
object or scene. The object or scene stays in the same place in world
coordinates.
To get an idea about "Zoom" ;)
landing simulation
The implementations vary depending on the toolkit being used.
The basic user interface is usually called a "slider". The user
places the mouse on the slide bar and drags the slide bar to
get the desired movement (pan, zoom, scroll, etc).
The GUI programmer must keep the object or scene world coordinates
unmoved and compute the new display requested by the user.
The Motif toolkit provides an option when a drawing area is created
to add horizontal and/or vertical scroll bars. When the user changes
the position of the slider in the scroll bar, the program gets an
event and receives a value that indicates the latest position of
the slide bar. The program must compute the display based on the input.
The computation is not automatic. Java provides a slider that can
be used for a scroll bar. OpenGL can be programmed to display and sense
the position of a slider.
The "look and feel" of Motif scroll bars and zoom slider are shown
in the following screen capture. The user drawing area is empty.
draw_gui.c Motif window setup, big!
May demo ../gui/proj5/draw
Assume the values are from 'smin' to 'smax' on all the slide bars with
the user placing the slide bar at 'spos'. The actual values of 'smin'
and 'smax' are usually settable by the application program.
Consider some point in 2D world coordinates x,y that is mapped to
screen pixel coordinates i,j by:
i = a*x + b*y + c (any complex mapping could be reduced to
j = d*x + e*y + f the six values a, b, c, d, e, and f)
This would be the nominal with all slide bars centered.
Assume all quantities floating point even though pixel coordinates
must eventually rounded to integers (or the intensity of the pixel
is computed based on the pixel coordinates).
The case where the user indicates scroll left, assume 'spos' as a value,
would result in:
new_i = i + (width*(spos-smin)/(smax-smin)-width/2)
More scrolling can be provided by an additional multiplicative constant
times the width. Generally there must be a fixed limit to how far the
user can scroll. Using this simple equation gives the user a double width
working area. To get a four width and height working area:
new_i = i + 2 * (width*(sposx-sminx)/(smaxx-sminx)-width/2)
new_j = j + 2 * (height*(sposy-sminy)/(smaxy-sminy)-height/2)
The case where the user can zoom in to see a larger version of
a smaller part of the working area, assume 'smin', 'smax' and 'spos'
are the slider values and the zoom factor is to be from 'zmin' to 'zmax'.
(you must limit both largest and smallest zoom, always positive)
The 'zval' zoom value is then:
zval = (zmax-zmin)*(spos-smin)/(smax-smin)+zmin
new_new_i = (new_i-width/2) *zval + width/2
new_new_j = (new_j-height/2)*zval + height/2
Note: In order to zoom, the i,j is translated to the center of
the screen, scaled, then translated back. If this is not performed,
then the zooming would also move the screen up and to the left.
The simple equations shown above become much more complex in 3D.
Yet, with a graphics tool kit, it reduces to the following:
To scroll left, move the position of the eye left while keeping
the direction vector unchanged.
To zoom in, move the eye closer to the object or scene.
The next lecture will cover the perspective and model transformations
in more detail, but for now it is sufficient to know that there
are two distinct transformations to get a point on a object in
world coordinates onto the display screen.
There is a perspective matrix that implements the frustum shown
in a previous lecture. This matrix is based on the location of the
eye relative to the scene, the direction the eye is looking, the
field of view, angle, the eye is viewing. The pan and zoom can
be accomplished in this matrix.
The model matrix implements the rotations, scaling and translations
of world coordinates into how the user views the scene. This does
not need to change with pan and zoom.
The scene itself is constructed in world coordinates. Any units of
measure may be used as long as all distances are in the same units.
e.g. microns, feet, kilometers, etc.
The example pilot.c is the basic
demonstration of moving the eye, pilot in this case, through all
six degrees of freedom. X, Y, Z, roll, pitch, heading.
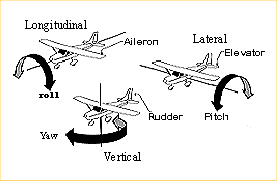Typically users are not given roll, pitch and heading so that
the horizontal scroll is X, the vertical scroll is Y and zoom is Z.
My "draw" program is not fully converted to Java. Starting with
draw.java main prog
Names.java selections
Rectangle.java one selection, rectangle
The Java program PaletteFrame.java calls
MyColorChooser.java that uses JSliders and looks like the image below.
python program to find r,g,b, for your color
color_chooser.py3 that uses mouse and looks like the image below.
ScrollDemo2.java looks like the image below.
Java automatic pop-into-existence scroll bars is demonstrated by
ScrollDemo2.java looks like the image below.
I personally prefer the scroll bars to be displayed all the time.
It is distracting to me when widgets such as scroll bars pop into
existence then pop out of existence.
My "draw" program is not converted to Python.
Are these good, average or poor examples of pan and zoom?
HW3 is assigned, select an object with mouse.
Possibly change color of selected object.
Example of mouse use in w2 series of examples.
Select.java simple color change
Best to use the language and tool kit you will use for your project.
<- previous index next ->
Many web sites on Java GUI, AWT, Swing, etc.
Many web sites on Python wx, tk, qt, etc.