MATH 481, Project 4: Population Models
Due on Friday November 8
Malthus' model
Verhulst's model
Verhulst's population model
Explain the idea behind Verhulst's population model:
\[
\frac{dp}{dt} = r\Big(1-\frac{p}{k}\Big)p.
\]
That is best done by starting from the idea of
a population's per capita rate of growth.
Show that the change of variable $q(t)=1/p(t)$ reduces
Verhulst's equation to a linear differential equation in $q$.
Solve that linear differential equation (hint: integrating factor)
with the initial condition $p_0 = p(0)$ and conclude that
\[
q(t) = \frac{1}{k}
+ \Bigl( \frac{1}{p_0} - \frac{1}{k} \Bigr) e^{-rk},
\]
whereby
\[
p(t) = \frac{1}{
\frac{1}{k}
+ \Bigl( \frac{1}{p_0} - \frac{1}{k} \Bigr) e^{-rk}}.
\]
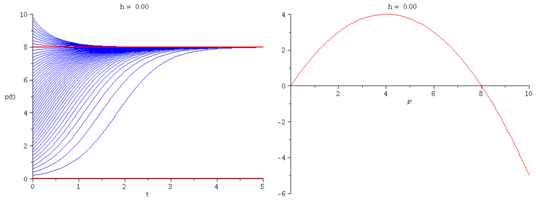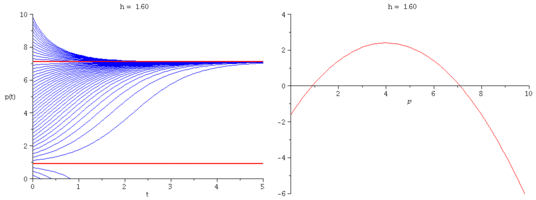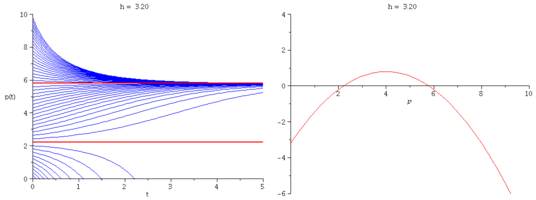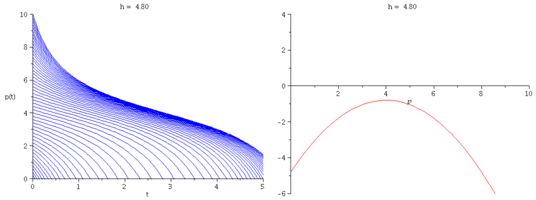
Verhulst's model with added quota harvesting
We modify Verhulst's model by imposing a constant harvesting rate $h$:
\[
\frac{dp}{dt} = r\Big(1-\frac{p}{k}\Big)p - h.
\]
- Plot representative solution curves for several values of $h$.
- Explain how one can tell what the solution curves look like
without solving the differential equation.
- What are the equation's equilibria? Are they stable or unstable?
- If the harvesting rate is increased beyond a critical value $h_c$,
the population is guaranteed to go extinct.
Find an expression for $h_c$ in terms of $r$ and $k$.
- This animation can give you ideas for your article:
Bibliography
Add bibliographic items (in your *.bib file) as needed.
Here are a couple of items to get you started.
-
Thomas Robert Malthus. Essay on the Principle of Population as it affects
the future improvement of society. With Remarks on the Speculations
of Mr. Goodwin, M. Condorcet and other writers.
1st ed. (Printed anonymously and ascribed to J. Johnson
in St. Paul’s Church-yard). London, 1798.
-
Pierre-François Verhulst, Notice sur la loi que la
population suit dans son accroissement,
Correspondance Mathématique et Physique, 10, 1838, 113–121.
Note: LaTeX code for the French character ç is \c{c} and é is \'{e}.
These (and more!) are on page 38 of Lamport's LaTeX manual.


