MATH 481, Project 4: Population Models
Due Wednesday April 26
Malthus' model
Verhulst's model
Verhulst's model with quota harvesting
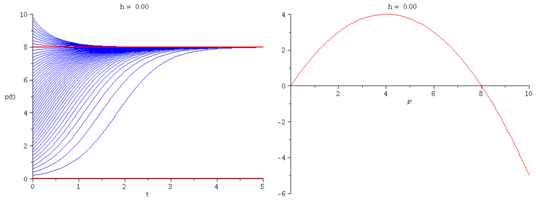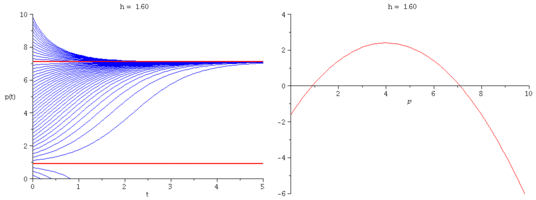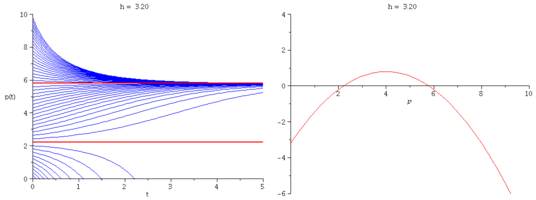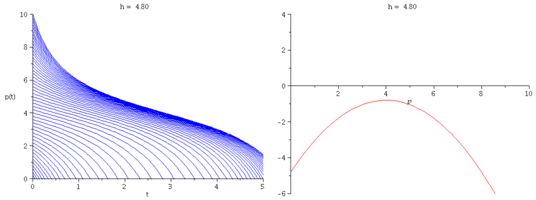
We modify Verhulst's model by introducing a constant harvesting rate $h$:
\[
\frac{dp}{dt} = r\Big(1-\frac{p}{k}\Big)p - h.
\]
- What is the critical harvesting value $h_c$ so that
the population has no chance of survival when $h > h_c$?
Express $h_c$ in terms of $r$ and $k$.
- Plot representative solution curves for several values of $h$.
- This animation can give you ideas for your article:
The predator-prey model
- Explain the logic behind the derivation of the predator-prey model
\begin{align*}
\frac{dx}{dt} &= ( a_1 - b_{11} x - b_{12} y)x, \\
\frac{dy}{dt} &= (-a_2 + b_{21} x - b_{22} y)y.
\end{align*}
- Describe the essential features of the system's
phase portrait and its equilibria. Qualitatively,
there are two distinct cases, depending on whether
$a_1/b_{11} < a_2/b_{21}$ or $a_1/b_{11} > a_2/b_{21}$.
Explain what that is so, and
show a sample phase portrait for each case.


