Project 3: QuadTrees: a Compact View

Due: Tuesday, April 10, 8:59:59pm

Links: [Project Submission] [Late Submissions] [Project Grading] [Grading Guidelines] [Academic Conduct]

Change Log

[Sunday Apr 1, 11:30am] The project description has been updated to include figures of quadtrees, as well as additions to the "Implementation Notes" section at the end. The only other part that has changed is an added parameter to the QTNode::remove() function, and a backwards-compatible modification to the declaration of QTNode::iterator::operator*(). The modifications to the function signatures are highlighted in orange.

Some of the provided files have been updated. Specifically:

Note: The project has been simplified to fit the 2-day delay in release, by providing complete implementations of the Point and BBox classes, as well as the class declarations for the QTNode iterator. The project description has been modified to reflect this. --JYP

Objectives

The objective of this programming assignment is to give you your first intensive taste of a tree-based data structure.

Introduction

For this project, you will implement a version of what is known as a quadtree. (Please read the Wikipedia page's intro section, then the sections on region quadtrees and point-region quadtrees; skip the rest.) One common application for quadtrees is in computer graphics, where it is used to encode a bitmap at varying resolutions while taking advantage of regions of homogeneity to save space. A bitmap is a m x n rectangular matrix of pixels, representing a picture with intensity or color values at each pixel. For simplicity of explanation, let use as an example a 512 x 512 pixel image, although you should be able to easily figure out how to handle arbitrarily-sized images. We will also assume that our sample image is black and white, with each pixel storing the value 0 for black or 1 for white. Now, imagine if the 512 x 512 image were all white, or all black: we could represent the image with a 262,144-element array, but that would be wasteful: we could instead somehow represent our image by summarizing it with some succinct, symbolic, data structure-y version of the statement "one giant 512 x 512-unit white pixel". How could we do that? And what if it isn't one giant white (or black) block--can we still take at least partial advantage of this summarizing technique? For example, be able to say: "the entire left half is black, but the upper right has some splotches of white in the following places"?

The answer is "yes", using something called a quadtree. Being a tree, it consists of nodes, each of which has up to 4 child nodes, all starting from a single root node. In the case of a uniform 512 x 512 white region, we would represent that as a single root node representing the region covering the X dimension from 0 thru 511, and the Y dimension from 0 thru 511, also, with a value of "1".

Now, what if the image wasn't a single uniform value? What if the pixels in the bottom-left quadrant--i,e. X and Y both in the range from 0 thru 255--were black, while the rest were white? We would then subdivide the original region into four equal-sized square quadrants, by taking our original root and giving it four child nodes. The root no longer technically holds a pixel value-- its children do. The child representing the bottom-left quadrant has a pixel value of "0" for black, while the other three child nodes have a value of "1" for white.

What about a more extreme case: an all-white image with a single black pixel at x=0/Y=0? Then the root node would be "empty" (i.e., not directly holding a value), but would have four child nodes. The three covering the top-left, top-right and bottom-right quadrants, would all hold the value "1", but the bottom-left would again be a non-value node, since the region it covers--{0-255, 0-255} would have a mix of 0's and 1's. So again, this level-1 node would have 4 kids, 3 of them holding values, but one child (again, the bottom-left) non-value because it covers both 0 and 1's. This pattern repeats down to level 9, where nodes/quadrants have shrunk to representing single pixels, and finally, even the bottom-left is all one color (trivially, since it contains only 1 pixel!). The idea is that you keep splitting nodes into smaller quadrants until a given quadrant contains only pixels of a uniform value.

Note that the above descriptions implies two additional properties: First, the tree must be full: every node has exactly 0 or 4 child nodes. Second, the splitting process implies that all squares at every level are aligned to a whole multiple of the square size at that level. For example, at a level where a square is 16x16 in size, it must start at some multiple of 16 in both X and Y dimensions.

The above is a called a region quadtree, since each node represents all the pixels in a square region of some size, and a value can be ascribed to any and every pixel. What if, however, you just wanted to store values associated with a small subset of the individual pixels (hereafter equivalently referred to as "points")? In that case, you would use another variant called a point-region quadtree.

The basic structure of a point-region quadtree is very similar to a region quadtree: every node still covers some square region of a power-of-2 dimension. However, what it represents is quite different. If it is an internal node, it does not implicitly store any information representative of values stored in any of points covered by that region. Instead internal nodes are merely subroots that each hold under it a sparse set of explicitly added points. So, if the user added the point {24, 53} to the tree, it would be at some node under the internal node covering the region {x = 0..63, y = 0..63}.

Next, actual data points are only stored at leaf nodes. However, we are not building a perfect tree: we do not split every node down to the very bottom level where every node represents a 1x1 square. Also, instead of subdividing into quadrants when a region contains more than one different pixel value, a point-region quadtree subdivides a node if it covers more than 1 stored point. As you add additional points, if it falls into a leaf node occupied by another point, that node must be split into 4 quadrants.

An aside here on numbering quadrants: in the rest of this document, in referring to the four quadrants (and therefore, the four potential children) of a node, we will refer to them using Roman numerals, numbering the quadrants I to IV in the order bottom-left, bottom-right, top-left, top-right.

So, let us say our current root node is an internal node representing the region {x = 0..63, y = 0..63}. If we added the point (50, 20), that would go into quadrant II (i.e., bottom-right) under that node, which would have bounds {x = 32..63, y = 0..31}. If there were no other points previously added into that quadrant, the current node would have no child for that quadrant (and the pointer would be NULL; we don't use dummy nodes). We would see the null pointer, create a new leaf node for that quadrant with bounds {x = 32..63, y = 0..31}, and store the point coordinates (50, 20) along with the user-provided associated data, in that leaf node. (Note that this implies leaf nodes have both a bounds as well as a specific point coordinate.)

Now, what happens if the user then adds the point (60, 20)? Starting again at the root, with bounds {x = 0..63, y = 0..63}, we would quickly calculate that {60, 20} also goes into quadrant II. What we find there is the leaf node we created when we inserted {50, 20}. Since we can hold only a single data point per node, we need to take the leaf node at quadrant II and turn it into an internal node. Then, both the previous point that was in that quadrant--(50, 20)--as well as the new point--(60, 20) must be moved into new child nodes of that node. However, they both map into the same 16x16 sub-quadrant IV: {48..63, 16..31}, So, we must once again convert that branch from a leaf to an internal node, and subdivide again: we finally end up with (50, 20) ending up in the 8x8 sub-sub-quadrant {48..55, 16..23}, while (60, 20) ends up in its sister sub-sub-quadrant {56..63, 16..23}, and we are done. Whew. Thank goodness we have computers to do this for us.

The above design creates as compact a quadtree as possible while still being a classic quadtree. (There are additional techniques that allow us to make it even more compact, such as compressed quadtrees, but that is way beyond the scope of this project.) The basic properties of our compact quadtree are:

  • points are stored at as high a level in our tree as possible, i.e., in the largest quad, that still does not cause it to have to share that quad with any other point.
    • That last two rules requires explanation. For the "leaf node cannot be an only child" rule, fixing that by effectively moving the leaf up a level is desireable because it is almost universally our goal with trees (I'm looking at you, splay trees!) to decrease the depth of nodes, and if we have a leaf node that is an only child, its point can be migrated up to the parent node and the node deleted, making the parent a new leaf node. (Note that this is not the same thing as moving up all "only children"! We only move up "only child" nodes that are leaves.)

    In an analogous manner, if a root node has exactly one child, that imples that (1) the tree is storing more than one point; and (2) all the points are in the same quadrant of the root node. In this case, the root node serves no purpose in facilitating search, unnecessarily increasing the height by one. We should just cut it off and make its solo child the new root. We should repetitively do this until we hit a new root that has multiple active child nodes. Note that a root node with 2 or more children, or even no children, or a tree with no root node at all, are all legal. [Diagrams to be added.]

    The CMSC 341 Twist

    No CMSC 341 project would be complete without a twist that renders it pointless to "re-purpose" code from other sources. Here's the Project 3 twist: Most quadtree implementations assume that the range of the X and Y dimensions are set a priori, and the root node's bounds cover this entire area. For example, for a graphics-oriented region quadtree, you know in advance that your quadtree needs to cover a 1024x1024 pixel area. If you have a 1920x1080 video frame, you would just increase your frame to 2048x2048 and waste some space.

    For this project, you cannot presume any particular maximum dimension. This, by the way, is why we can have the rule about pruning the root of the tree, since the root does not have to a priori cover any particular sized region. This, however, raises the complication of what to set the bounding box to for the very first node: the first root node that is created when the user adds the first point? Actually, the consequences of your choice of initial bounding box do not kick in until you add the second point. Think through for yourself why this is a complex issue.

    A second complication from not having a preset maximum range is that whatever bounding box the current root covers, the user might ask to add a new point that is outside that area. The extreme solution--to set the root's bounding box to the largest possible legal square-- won't work because as soon as you have added multiple points, it is likely that those points are in the same general area, which will be one particular sub-sub-sub-sub-...-sub-quadrant of the huge root. The root-pruning rule will immediately remove most of the path leading from the root, leaving a new root that has a much smaller bounding box. This again leaves you with a situation where you will likely be adding a new point outside the root's current area. This means you must be ready to grow a tree at the top no matter what. This is not terribly complicated: just requires some careful thought and work.

    Compact Quadtree Maintenance

    The quadtree you design for this project must be kept as compact as possible. By "compact", we mean every point must be stored at a node as close to the root as possible while still obeying the rules of a proper quadtree (i.e., points stored only at leaf nodes, all nodes having bounding boxes, boxes at any given level being a quadrant of its parent's bounding box). The following trees would therefore be illegal: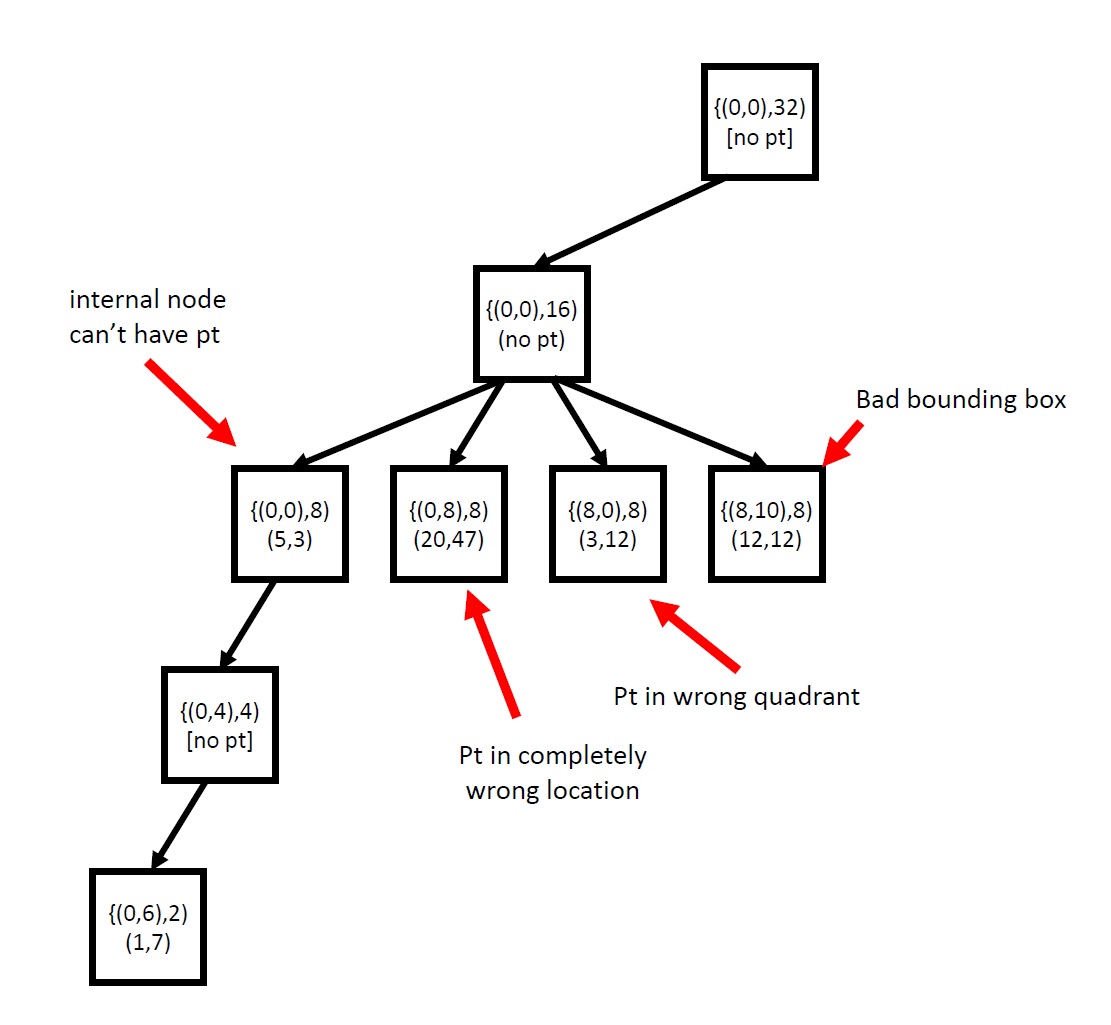

    Fig. 2: An illegal quadtree

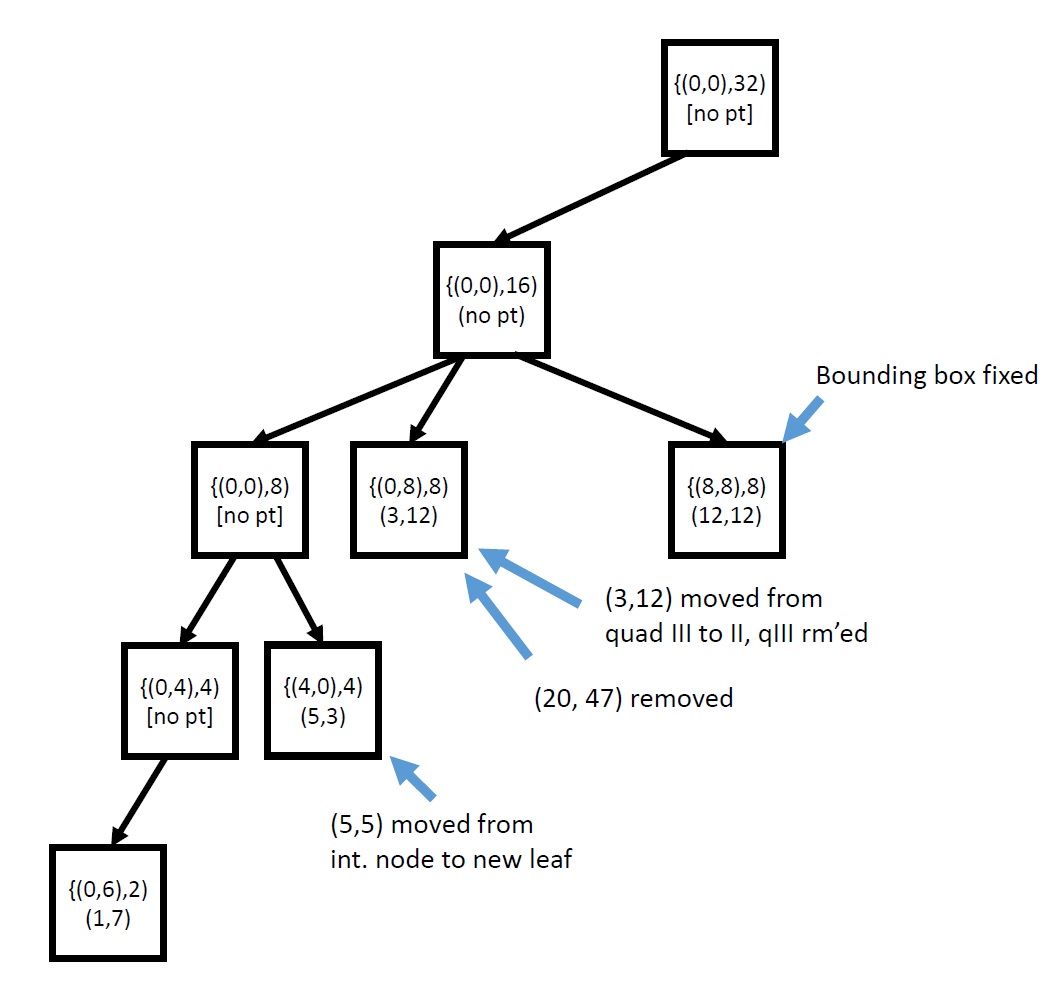
    This tree would be legal, but not as compact as possible, so not acceptable for this project:

    Fig. 3: A legal but not fully compact quadtree

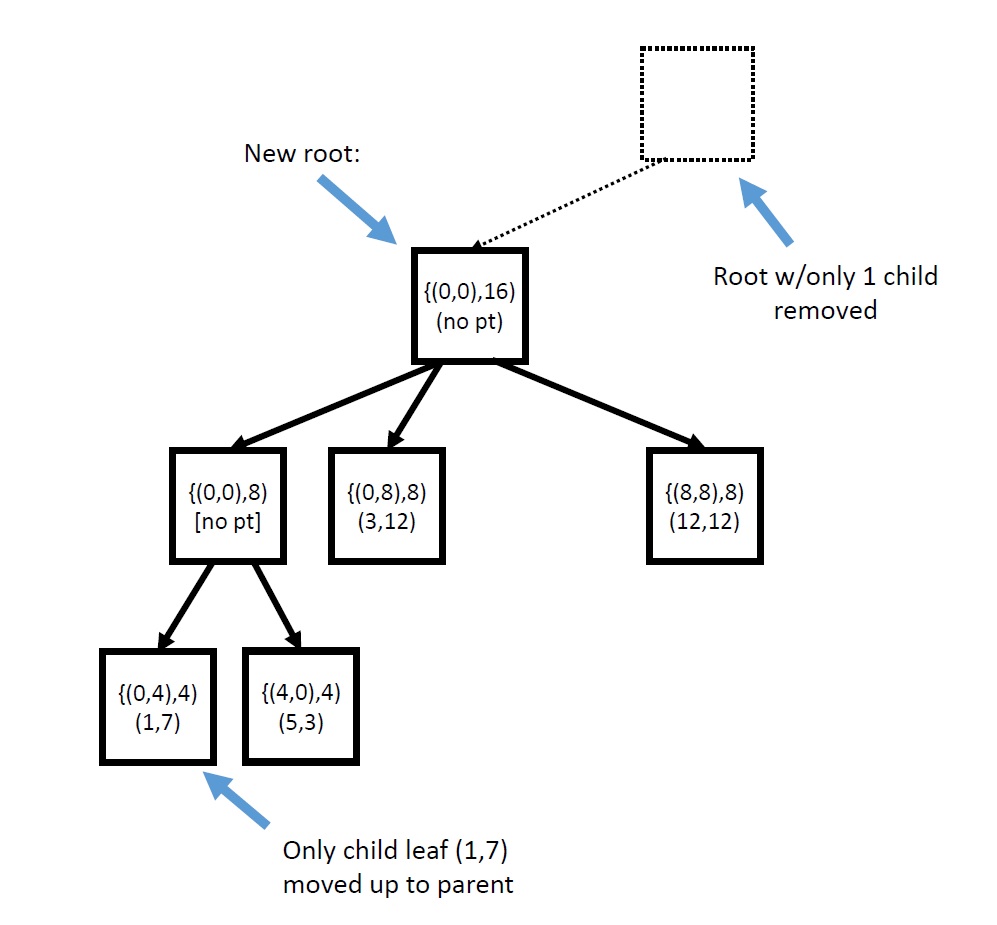
    This modified tree would be more compact because the leaf nodes have been brought up as far as possible while still being legal; and

    Fig. 4: An optimally compact quadtree

    would be the most compact, since pruning the root kept the tree legal, but decreased the depth of all nodes. This shows that the root-pruning is an implied indirect requirement of the compactness rule. The last tree above would get you a good grade on the project (assuming your code looks good, of course).

    These properties must be maintained by the operations that modify the tree. For example, when adding a new point, you just drop the point into the first empty quadrant you find as you search down the tree. If you do this correctly, no property will be violated.

    Removing points is another matter. This can trigger violations of one or more of the compactness properties. It is your job to think about what kinds of deletions might cause what kinds of violations, and then test for and handle those scenarios. (For example, the point that was removed must have been stored at a leaf node (requirement). If it had a sibling leaf node, that node might now be the sole child of their parent, which means it needs to be moved up, again to maintain compactness. Think about any other scenarios. This project requires less coding, but more thinking and design. First, removing a node requires that you removed the leaf node it was stored in. However, that would make it's parent potentially a leaf. You should either test for and handle this, or prove to yourself this cannot occur.

    Assignment

    Note: Running time is one of the most important considerations in the implementation of a data structure. Programs that produce the desired output but do so in an excessively inefficient manner are considered substandard implementations and will receive deductions during grading.

    Your assignment is to implement a point-region quadtree data structure as described above, for holding a collection of distinct 2-D points (consisting of X and Y coordinates), each point carrying associated data (for this project, just a simple int, although real-world applications would typically store something more complex). You must implement the two primary classes QTree and QTNode yourself. You are allowed to use simple STL classes like pair and vector inside your own class implementations to handle simple lower-level needs. At the top, you will design a QTree class (short for "QuadTree") that has definitions for all of the member functions described later in this section. Functionally, it implements the upper half of all of the quadtreee functionality, but data-wise, it is primarily a holder for a pointer to the root node, which is of type QTNode. You are free to add other function and data members to support the operations and runtimes required by this project.

    The QTree object will point to the root node of a quadtree constructed of instances of the QTNode class (for "QuadTree Node"). You will be also be defining this class almost from scratch. You have a lot of freedom in designing this class, as long as it implements the required functionality. For instance, it must hold pointers to the nodes that represent its four child quadrants, but how you store and represent those is up to you. You may also add other data members as necessary to implement the necessary functionality.

    One additional element of the project is that since we give you freedom to implement your pointers-to-child-quadrant-nodes any way you please, it becomes difficult to write a grading program that analyzes your quadtree. So, you must write an iterator nested class for the QTNode class that allows us to iterate over the 4 child pointers. The class should be QTNode::iterator, and QTNode should have functions QTNode::begin() and QTNotde::end() that act as such functions should for a typical iterator implementation. Code like the following: 

        QTNode *qtnode;

    ... // code that makes qtnode point to some QTNode

    for (QTNode::iterator it = qtnode->begin(); it != qtnode->end(); qtn++) {
        QTNode *kid_qtnode = *it;
        if (kid_qtnode != NULL) {
            // Code here to do stuff with that child node ptr
        }
    }
    Note that the above loop should always run exactly four times, and return the child QTNode pointers for the four quadrants in the order specified earlier, some possibly NULL.

    At the lowest level, you will use two classes we are providing to let you represent 2-D X/Y points (the Point class), as well as the bounding boxes (the BBox class). You will use the Point class to store the point in leaf nodes, and will use the BBox class to represent the bounding box for all nodes. (In fact, the BBox class itself uses the Point class internally for one of its data members.) Since all nodes--internal as well as leaf-- are of type QTNode, the data members m_point and m_data of a node will simply go unused when it is acting as an internal node; we won't worry about wasting that space.

    This assignment specifies the interface between the main program and your QTree implementation, and also specifies a set of required functions for the QTNode implementation, but you are free to design the internals of the class as you wish, subject to some requirements below. In particular, you are not provided with a only a very partial header file for the QTree and QTNode classes. You are provided complete implementations for the Point and BBox classes.

    Note that design is part of the grading criteria, so you do need to apply good design principles to your data structures. However, in your design, you must adhere strictly to each and every requirement and specification listed below, or the grading process will fail and you will get significant deductions.

    Requirement: At the end of any and all QTree operations, the resulting quadtree should always be a valid compact quadtree (see properties above).

    Requirement: You must complete the class definition for the QTree class, as provided in the file QTree.h. You cannot modify any of the existing data members, including their names, types, and public visibility, but you can add any additional data members as needed. You cannot modify or remove any of the existing member function declarations, but you can add additional helper functions to facilitate your implementation. The class definition must be modified in-place in the provided skeletal file QTree.h and the member functions must be implemented in a file called QTree.cpp, which is not provided and which you must create in its entirety.

    Requirement: Your QTree class must use the field named m_root to store the pointer to the QTNode that is the root of the entire quadtree. In other words, you must leave the following declaration as-is and use it:

    QTNode *m_root;

    Requirement: You must complete the class definition for the QTNode class, as provided in the file QTNode.h. You cannot modify any of the existing data members, including their names and types, and public visibility, but you can add any addtional data members as needed. You cannot modify or remove any of the existing member function declarations, but you can add additional helper functions to facilitate your implementation. The class definition must be modified in-place in the provided skeletal file QTNode.h and the member functions must be implemented in a file called QTNode.cpp, which is not provided and which you must create in its entirety.

    Requirement: The QTNode class will define the data stored in each node of your quadtree, both internal and leaf. You must leave the following data member declarations as-is:

    BBox m_bounds; // The bounding box for this node Point m_point; // If leaf node (i.e., no kids), m_point, m_data hold the int m_data; // actual point and data value the user inserted.

    Requirement: You must add one or more data members to the QTNode class to support storing the 4 pointers to child QTNodes, one for each quadrant. The child nodes must be position-specific.

    Requirement: You must add one or more data members to the nested class QTNode::iterator (we provided a skeletal version in QTNode.h) to support iterating over the pointers to the four child nodes in the exact order specified earlier. The iterator should return NULL for children that do not exist.

    Requirement: You are given the class definition and implementation of the utility classes Point and BBox to assist you in your implementation. The are provided in four files:

    You may not change these files in any way, nor should you submit them. We will replace them with our own versions in any case.

    Requirement: You must leave the pre-existing public data members of both QTree and QTNode classes as public. We will be using this to poke around in your implementations and validate them for grading purposes. We will also be using your iterator implementation heavily for grading, so it is essential that it work correctly!

    Requirement: Your code must not have any memory leaks. When you run your code under valgrind on GL, it must report:

    All heap blocks were freed -- no leaks are possible

    Requirement: Your implementation must be efficient. Since quadtrees are worst-case O(n) for most operations, what we are looking for are unnecessarily expensive design choices. One specific example: we pointed out in the description above that when you insert the first point, and therefore first node, into an empty tree, you must decide what to set its bounding box to. If you set its dimension to be the largest possible size (i.e., largest power-of-2 value you can store in an unsigned int), then if you insert another point right next to it (e.g., you first insert (x,y), then (x,y+1)), then what might happen, depending on your implementation, is that you initially create a very long single-child-all-the-way-down branch from the root to the bottom-most level. This would not be compact, so you must then prune the root all the way back down to almost the very bottom. This will result in a large number of unnecessary operations, as a more efficient implementation would figure out a way to directly create most compact tree on the second insertion (HINT!). In other words, for this project, efficiency is less O() and more good design.


    Specifications

    In addition to the requirements above, your QTree class must have the following member functions with the specified functionality and running times:

    1. A default constructor that initializes a QTree properly. It should run in O(1) time.

    2. A destructor that cleans up the entire tree, recovering all dynamically allocated space. Your implementation must not leak memory.

    3. A member function to insert a 2-D data point with associated value into the appropriate position in a QTree. If the point already exists, replaces the associated value. Returns true if a new point was added.

      bool add(const point &pt, int data);

    4. A member function to remove a point from a QTree, returning true if the point was actually found and removed.

      bool remove(const Point &pt);

    5. A member function to search for a given point in a QTree, returning a boolean, true if an item was found, passing back its associated data value in the by-reference parameter data. If not found, returns false, and does not modify data

      bool find(const Point &pt, int &data);

    6. A member function to search for all points in a given range in a QTree. The range is specified by the bounding box passed in the parameter region, where all points with X-values between region.m_bL.x and region.m_bL.x + region.m_dim - 1, inclusive, and similarly defined range for Y-values are searched for. All matching Point's are returned by being added to the end of the vector parameter found. Note: the data associated with each point is not returned: a call to findPoints() would be followed up with a series of calls to find() to then fetch the associated data. The number of Points found and added to found on just this call is returned. Note that this allows us to create an empty vector, call findPoints() on several different regions, and create a single long vector of the concatenated results. YOu do not have to check for duplicates in found which might result from searching overlapping regions on successive calls.

      int findPoints(const BBox &region, std::vector<Point> &found);

    7. A debugging member function:

      void dump() ;

      The dump() member function should print out the contents of the entire quadtree, exactly in the format shown in the sample output (see "Provided Files" section below). You should implement dump() in the most reliable manner possible (i.e., avoid calls to member functions which might themselves be buggy). The format we chose will allow us to provide a script that will allow the output to be reformatted in a nice nested indented format that will make analysis easier for your debugging, and will also allow us to analyze the structure for grading, so it is critical that you get it exactly right..
    Then, your QTNode class must have the following member functions with the specified functionality and running times:

    1. A default constructor that initializes a QTNode properly. It should run in O(1) time.

    2. A destructor that cleans up the entire (sub)quadtree rooted at the node, recovering all dynamically allocated space. Your implementation must not leak memory.

    3. A member function to insert a 2-D data point with associated value into the appropriate position under the sub-quadtree. If the point already exists, replaces the associated value. Returns true if a new point was added.

      bool add(const point &pt, int data);

    4. A member function to remove a point from a (sub)quadtree, returning true if the point was actually found and removed. Note that remove() is recursive, and is a member function invoked on a node. That means a node cannot delete itself before returning. This implies a parent must wait until a recursive call to remove() returns, then examine the child node to determine whether it should be deleted. Since it is easier for the child to know it just became empty than for the parent to assess this after the fact, we have modified the function signature by adding a "bool &empty" param to allow a recursive call to remove() to inform the caller the child node just became empty, and should be deleted. This is a feature you are not in any way obligated to use: the caller can just pass in a dummy int variable, and your remove() implementation can ignore it.

      bool remove(const Point &pt, bool &empty);

    5. A member function to search for a given point in a (sub)quadtree, returning a boolean, true if an item was found, passing back its associated data value in the by-reference parameter data. If not found, returns false, and does not modify data

      bool find(const Point &pt, int &data);

    6. A member function to search for all points in a given range in a QTree. The range is specified by the bounding box passed in the parameter region, where all points with X-values between region.m_bL.x and region.m_bL.x + region.m_dim - 1, inclusive, and similarly defined range for Y-values are searched for. All matching Point's are returned by being added to the end of the vector parameter found. Note: the data associated with each point is not returned: a call to findPoints() would be followed up with a series of calls to find() to then fetch the associated data. The number of Points found and added to found on just this call is returned. Note that this allows us to create an empty vector, call findPoints() on several different regions, and create a single long vector of the concatenated results. YOu do not have to check for duplicates in found which might result from searching overlapping regions on successive calls.

      int findPoints(const BBox &region, std::vector<Point> &found);

    7. A debugging member function:

      void dump();

      The dump() member function should print out the contents of the entire (sub)quadtree rooted at current node, exactly in the format shown in the sample output. Note that dump() can easily be designed to be recursive, so you only have to print out the node-specific info, then recursively call dump() on each non-NULL child. (Note: same warnings about the importance of this function as for QTree::dump() above.)

    8. The iterator support functions for performing iteration over the list of child QTNodes:

      iterator begin(); iterator end(); iterator::iterator(); bool operator==(const QTNode::iterator &other); bool operator!=(const QTNode::iterator &other); iterator &operator++(); // Prefix: e.g. "++it" iterator operator++(int dummy); // Postfix: "it++" QTNode * &operator*();

      These are all the standard iterator-related support functions, and should not need to be further described. The operator*() function's declaration was updated to return by-reference, to allow use on left-hand side of assignment. (e.g.: "*it = new QNode;") This update is Backwards-compatible: no changes are required to any code you've already written other than modifying the signature.

    Provided Files

    In the directory 00Proj3 under the submission directory, copies of all of the necessary files have been made available:

    Implementation Notes

    We list some recommendations and point out some traps and pitfalls (note much of this is duplicated from previous projects):

    Testing

    Again, we are provided fairly simple test programs to get you started. To fully test your classes, you will have to write your own additional test programs. The test program we will provide is just to make sure that your code will compile with the grading programs. Rest assured that the grading programs will exercise your code vigorously.

    Test programs:

    It also might be useful, and fairly simple, for you to adapt the interactive test code we provided for Project 1 to help you debug this project, by allowing you to add pts, remove pts, etc. interactively and test the results.

    How to Submit

    You need to submit the following files: