Project 2: Square Lists, Round 2
Due: Monday, March 12, 8:59:59pm
Links: [Project Submission] [Late Submissions] [Project Grading] [Grading Guidelines] [Academic Conduct]Change Log
[Monday Mar 5, 17:50pm] There was a typo in the runtime for the indexOf() function: it originally read "O(m√n"; it has been fixed to say: "O(√n) time. for the DNode class had a typo in it: the field m_data should be of type Int341 and not of type Int341 *; i.e., it should be an actual Int341 object and not a pointer to one. Also, a corrected version of the test file p2comptest.cpp has been posted, which fixes the "Int32" typo as well as a missing variable declaration and the lines which use it. The logic/functionality has not changed.
[Wednesday Feb 28, 09:59pm] The required data member declarations for the DNode class had a typo in it: the field m_data should be of type Int341 and not of type Int341 *; i.e., it should be an actual Int341 object and not a pointer to one.
Objectives
The objective of this programming assignment is to give you significant hands-on practice implementing linked lists, and with thinking about O() runtimes of algorithms on complex data structures.Introduction
For this project, you will implement another variant of the square list data structure, thematically similar to the square list you implemented for Project 1. However, for this project, our square list will be implemented using multiple linked lists combined in an interesting new way.
As mentioned before in the intro to Project 1, a square list is usually implemented as a linked list of linked lists where each sublist is guaranteed to have O(√n) items: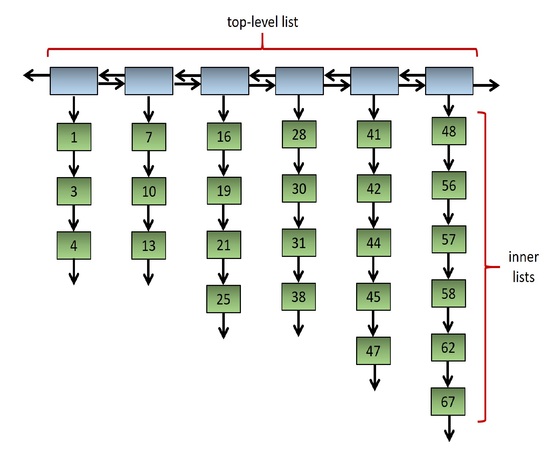
Fig. 1: A typical square list.
Figure 1 shows a typical square list of 25 integer values. The positions of the items are important. The ordering of the items in this example is: 1, 3, 4, 7, 10, 13, 16, 19, 21, 25, 28, ..., 58, 62, 67.
The idea of a square list is that we want to keep the length of the top-level and of all the inner lists bounded by O(√n). That way we can find the ith item of the list in O(√n) time. Additionally, most square lists are kept sorted, so that the same O(√n) time applies to finding items by their value. For example, if we want to find the 9th item in the list, we can progress down the top-level list and check the length of the inner lists. We know the 9th item cannot be in the first inner list, since it only has 3 items. It also cannot be in the second inner list, since the first two lists combined only has 6 items. Instead, we can find the 9th item of the square list by looking for the 3rd item of the third inner list, which turns out to be 41.
Similarly, if we are looking for the value X in a sorted square list, we can walk down the top-level list and check the first item in each sublist, and when we hit a head value that is greater than X, we know we should search the immediately preceeding sublist.
To accomplish either of these searches in O(√n) time, we need to be able to determine either the length of each inner list, or whether the inner list contains the range of values our searched-for datum is in, respectively, in O(1) time. Now, we still have to walk linearly over elements in the top-level list. In the worst case, we have to search through O(√n) items of the top-level list before we find the inner list that potentially holds the item of interest. An additional O(√n) steps will allow us to find the desired item in that inner list, since the length of each inner list is also O(√n).
The main difficulty in maintaining a square list is that as we add items to and remove items from a square list, the length of the inner lists can change. This can happen in two ways. First, obviously, when we add items to or remove items from an inner list, the length of that inner list changes. Secondly, the length of an inner list relative to O(√n) can also change when we add or remove items elsewhere in the square list because doing so changes the value of n. For example, the 5th inner list in Figure 1 has 5 items. This happens to be exactly √25. If we removed all 10 items from the first 3 inner lists, that would leave us with only 15 items in the entire square list. After the removals, the length of the last inner list becomes bigger than √n even though the length of that list didn't change. The length becomes bigger than √n because √n dropped from √25 to √15, and 5 > √15.
Square List Maintenance
Our goal is to make sure that the top-level list and all the inner lists have lengths bounded by O(√n). It is too expensive to require that our square list always has √n inner lists, each with √n items. Instead, we maintain the following two conditions:
- Condition 1:
- Every inner list has ≤ 2 √n items.
- Condition 2:
- There are no adjacent short inner lists, where short is defined as having ≤ √n/2 items.
Notice that neither condition says anything about the length of the top-level list. Instead, we claim that if Condition 2 holds, then the top-level list cannot have more than 4 √n items. Too see this, suppose the contrary. That is, suppose that the top-level list has more than 4 √n items. (Yes, this is the beginning of a proof by contradiction.) Then, there must be more than 2 √n inner lists that are not short (otherwise, two of the short inner lists would be adjacent). Thus, the total number of items in these non-short lists must exceed 2 √n × √n/2 = n. This is a contradiction because n is the number of items (by definition) and cannot exceed itself. Therefore, the number of inner lists (and thus the length of the top-level list) must be bounded by 4 √n.
These observations allow us to maintain the O(√n) bounds on the lengths of the top-level list and the inner lists using the following procedure:
Consolidate:
- Traverse the top-level list.
- Whenever an empty inner list is encountered, remove that inner list.
- Whenever two adjacent short inner lists are encountered, merge them into a single inner list. (See Figures 2 and 3.)
- Whenever an inner list is found to have more than 2 √n items, split them into two lists of equal length. (See Figure 4.)
Some notes on the Consolidate procedure:
- Our strategy for this project is to run Consolidate after every operation that adds an item to or removes an item from the square list.
- When two short lists are merged into one, the order of the items in the square list must not change. Since our entire list is in sorted order, the elements in each inner list must have been in order, and the same must be true of the resulting merged list.
- We need the data structure for the inner list to support a merge operation in constant time. We can merge two singly-linked lists in constant time if we maintain a tail pointer. However, for this project, we have something better in mind, to be revealed shortly.
- In Figure 4, the inner list that is too long has an even number of items. If a long list has an odd number of items, then after the split, one list will have one more item than the other. This does not affect the asymptotic running time.
- When a long list is split, the order of the items must be preserved. (See Figure 4.)
- Without any splits, the total running time for the Consolidate procedure is O(√n), because we can merge short lists in constant time.
- The split step can be costly because it takes O(t) time to split an inner list in half, where t is the length of the inner list. We can show using amortized analysis that splits do not happen very often. The proof is not hard but is beyond the scope of this course. The amortized analysis gives an amortized running time of O(√n) for most of the list operations. The amortized analysis shows that any mix of m list operations will take a total running time of O(m√n). Thus, the amortized time for each of the m square list operations is O(√n). Although, it is tempting to think of the amortized running time as an "average" running time, this is not accurate because the amortized analysis does not depend on the sequence of operations being "nice" or "average" in any way. Even when an adversary chooses the nastiest sequence of operations which results in the maximum number of splits, the total running time for that sequence of m operations will still be bounded by O(m√n).
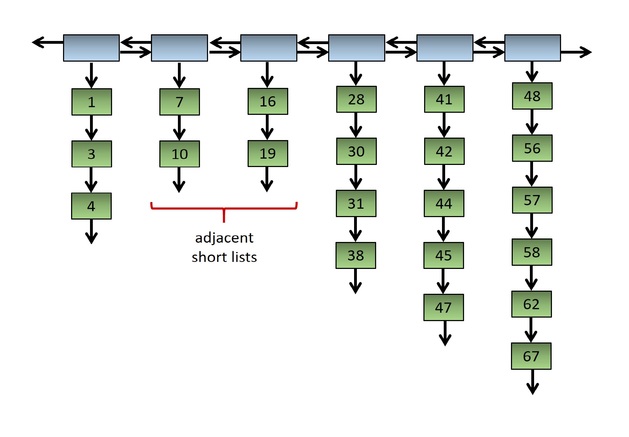
Fig. 2: A square list with adjacent short inner lists. Note that 2 < √22/2 ≈ 2.345.
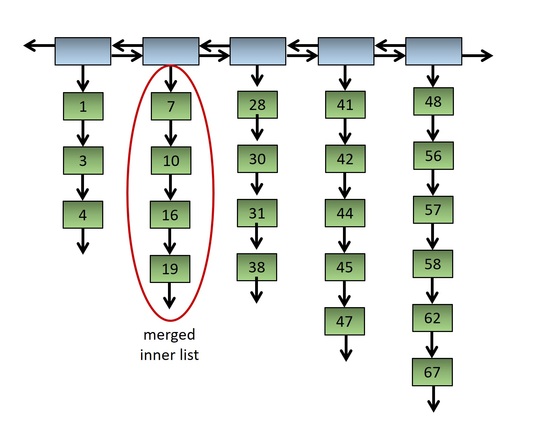
Fig. 3: Adjacent short lists merged.
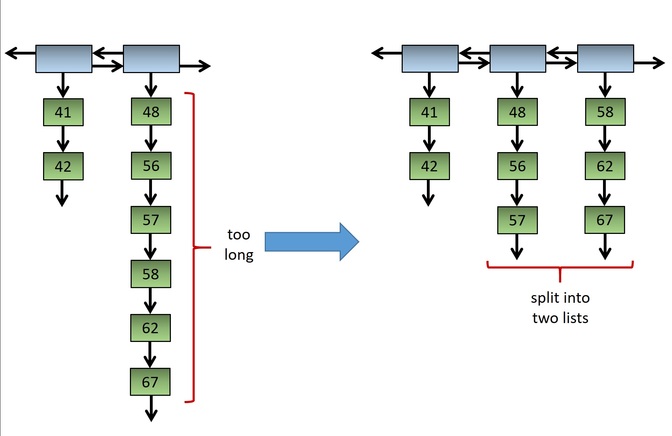
Fig. 4: A long inner list split into two lists. Note that 6 > 2 √8 ≈ 5.657.
Our Twist on the List-of-Lists
The purpose of the square list is increased efficiency: improving the O(n) time of traditional straight linked list to O(m√n for many of the operations. The externally visible interface is still that of a simple sorted sequence. You insert items into the sequence without regard to specifying the position to insert it into. You retrieve items by value, or by position within the entire list. There is no external indication that the shape of the internal implementation is 2-dimensional or square.
In the usual implementation, as described in the earlier section of this document, a top-level linked list acts as a container for contiguous pieces of the sequence, each stored in a separate sublist. (see Fig. 1)
However, an alternative way to think about what the top-level list is providing is to think of the sequence as a single, continuous linked list. Starting with the conventionally structured square list shown in Figure 5:
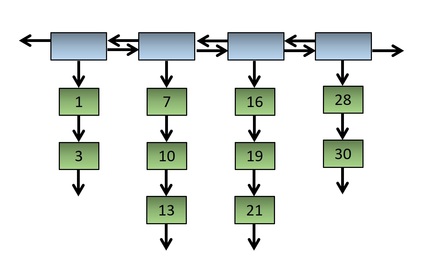
Fig. 5: Another typical square list.
if for each inner list, instead of terminating with a NULL pointer, we chained it to the next inner list by making the last node point to the first node of the next inner list, we would get the arrangement shown in Figure 6:
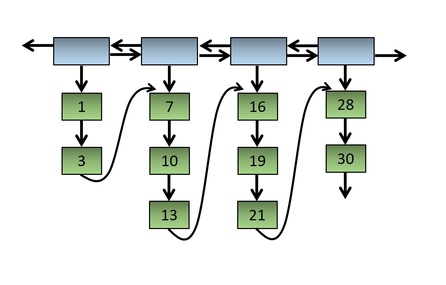
Fig. 6: Chaining the inner lists
If we were now to redraw the diagram "pulling the inner list chain taut", as it were, we would end up with Figure 7:
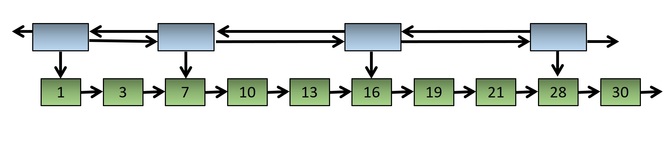
Fig. 5: Chained square list: another perspective
This last figure makes it clear that the top-level list elements are there to give us faster access to specific, approximately evenly-spaced markers along the ordered sequence of values, so that we can skip past whole chunks of the sequence and zero in on one particular subsequence of values (i.e., one particular inner list) in our sequence quickly, as opposed to serially examining, or counting, each and every item in our sequence.
So if the main benefit of the square list is to establish these evenly spaced markers, why not actually implement them that way? That is what we will do. In this project, we will implement our primary sequence of values not as a collection of separate inner lists, but rather as one long, sorted singly-linked list of data nodes. Then, on top of this, we will build another, top-level linked list, where each node will have as its "data" member a pointer to one of the nodes in the main data list. The top-level list will be implemented as a doubly-linked list.
It's worth pausing here to define some terminology. We will refer to the singly-linked list that contains all the actual data as the data-level list. Similarly, we will refer to the top-level list--the doubly-linked list that holds the pointers to interspersed points along data-level list--as the index-level list. Also, when we talk about an "inner list" and "inner list length" in the following sections, we are talking about those elements in the data-level list that are in the range from a node pointed to by one index-level pointer to the next, and the physical count of the nodes in that range, respectively.
With the above structure in mind, the operations previously defined for the Consolidate procedure are conceptually the same, but the implementation is different, and arguably, simpler. Traversing the top-level list is the same as before. However, the definition of an empty inner list has changed: it is when an index-level node is pointing to the exact same data-level node as its neightbor index-level node. Merging two inner lists consists of simply removing the second index-level node from the index-level list. Lastly, splitting is implemented by just inserting a new index-level node pointing to a data-level node halfway down the original inner list. So, there is no actual splitting or merging of discrete sublists: there is just inserting or removing nodes in the index-level list. The data-level linked list is only modified when actual data is added or removed.
Assignment
Note: Running time is one of the most important considerations in the implementation of a data structure. Programs that produce the desired output but exceed the required running times are considered wrong implementations and will receive substantial deductions during grading.
Your assignment is to implement a square list data structure as described above that hold integer values (more on "integer" later). You will be using a combination of self-implemented and STL classes. At the very top, you will design a SqList class that has definitions forall of the member functions described later in this section. Its primary data member will be the index-level list, stored in a data member named "m_iList" (for "index list"). This data member is the doubly-linked list that comprises the index-level list, and must be an instance of the C++ STL list templated container class. Other data members will definitely be necessary to support the operations and runtimes required by this project.
Each element in the index-level list will be an object of the INode class (for "Index-list Node"). You will be defining this class from scratch. You may design this as you wish, but you a mandatory member is a pointer to the data-level node it is indexing into. That data member must be named m_dNode and be of type DNode*. Additionally, you will definitely need to define various supporting data members to help achieve the required runtimes.
At the lowest level, you will have the singly-linked list of actual data-level nodes. Each node will be an object of the DNode class (for "Data-list Node"), which you will define from scratch. The actual data, of type Int341, will be stored in this object, in a field named m_data. Additionally, you will define the link to the next node as m_next. You may add any additional member data and functions as desired.
This assignment specifies the interface between the main program and your square list implementation, but you are free to design the class as you wish, subject to some requirements below. In particular, you are not provided with a header file for the square list class. Note that design is part of the grading criteria, so you do need to apply good design principles to your inner list data structure. However, in your design, you must adhere strictly to each and every requirement and specification listed below, or the grading process will fail and you will get significant deductions.
Requirement: Your square list class must be called SqList. The class definition must be placed in a file called SqList.h and the member functions must be implemented in a file called SqList.cpp. File names are case-sensitive on GL.
Requirement: Your square list class must contain the index list defined as an instantiation of the templated std::list class. Your SqList class definition must have the declaration:
Requirement: The INode class will define the data stored in each node of your index-level list. The INode class definition must be placed in a file called INode.h and the member functions must be implemented in a file called INode.cpp. The class must have at least the following data declaration:
Requirement: Your data-level list must be implemented as a linked list of DNode instances. The DNode class definition must be placed in a file called DNode.h and the member functions must be implemented in a file called DNode.cpp. The class must have at least the following two data declarations:
Requirement: You are given the class definition and implementation of the Int341 class in Int341.h and Int341.cpp. You may not change these files in any way.
Requirement: You must have a member function named consolidate with the following signature in your SqList
Requirement: You must have a public member function named inspector with the following signature in your SqList class definition:
Requirement: Your code must not have any memory leaks. When you run your code under valgrind on GL, it must report:
Requirement: Your implementation must be efficient. The running time for n operations with n data items stored in the SqList must be O(n √n). (See "How to Submit" below.)
Specifications
In addition to the requirements above, your SqList class must have the following member functions with the specified function signatures and running times:Implementation Notes
Before we list some recommendations and point out some traps and pitfalls, let's discuss Int341 and why we have it. One of the pitfalls of using STL container classes (and object-oriented programming in general) is unintentional copying. The Int341 class has just an int for its payload data. Its purpose is to allow us to track the number of times that the constructor, copy constructor, destructor and assignment operators are called. Consider the following main program that uses 5 different methods for retrieving the last item of a list<Int341> list. The report() member function of Int341 prints out the number of times that Int341 objects were created, copied and destroyed. (See Int341.h and Int341.cpp.) Note that the last two methods, using a reference and a pointer respectively, do not increase the number of calls.
Output:
The main point here is that your consolidate() function should not copy any data items. In particular, when you split and merge inner lists, you should not increase the number of calls to the Int341 constructor, copy constructor, destructor or assignment operator. You can check this by calling Int341::report() before and after you call consolidate.
Now we list some recommendations and point out some traps and pitfalls:
- Apply the incremental programming methodology. Implement one or two member functions and fully debug them before writing more code.
- Carefully study the documentation for the STL list container class (e.g., here). Pay attention to the parameters, return values and the effect that a call would have on iterators. Make sure that you understand iterators and how to use them. There are often several ways to do the same thing with these member functions. You should choose the option that is more efficient and avoids copying.
- If you are not sure what a list member function does, write a small program that uses the function to test it.
- Review what the list destructor does and when it is invoked.
- The consolidate() function is the hardest. Think through the logic carefully before you code. For example, it is possible to have 3 short inner lists in a row. (How?) Would your consolidate() handle this case correctly? What are some other "weird" cases?
Testing
In Project 1, you were given an extensive suite of test programs. This is to provide you with an example of how you can test your code. For this project, you will have to write your own test program. The test program we provide below is just to make sure that your code will compile with the grading programs. Rest assured that the grading programs will exercise your code vigorously.
Test programs:
- Program that uses every required member function in the
SqList class. This includes an implementation of
inspector() that checks that your inner lists are not too
long and do not have adjacent short lists.
p2comptest.cpp
p2comptest.txt - Programs for timing trials
p2timetest1.cpp
p2timetest2.cpp
p2timetest3.cpp
How to Submit
You need to submit the following files:
- SqList.cpp and SqList.h
- INode.cpp and Inode.h
- DNode.cpp and Dnode.h If for some reason you want to define new classes and additional functions, put all the declarations in SqList.h and all the implementations in SqList.cpp.
- Suppose you start with an empty square list and keep inserting items in the front of the list. When does the first merge occur?
- What is the smallest number of items you can have in a square list that has 11 inner lists?
- Do we ever encounter long inner lists that have to be split (other than the first inner list) if we only allowed insertion and removal at the beginning of the list?
- After you split an inner list, is it possible that the same inner list has to be split again after the very next square list operation? after two operations? when could the next split occur?
- Can you ever encounter 3 short lists in a row during the Consolidate procedure? Does it matter? and should you write code whose correctness depends on the answer to these questions?
Do not submit Int341.h or Int341.cpp since those should not have changed.
We need a C++11 compiler to correctly perform the timing runs for this project. Instead of logging into the GL machines, log into one of fedora1.gl.umbc.edu, fedora2.gl.umbc.edu or fedora3.gl.umbc.edu. You can use the same username and password that you use on GL. The directory structure is the same as on GL. If you have customized your shell environment, some of your customizations might be broken, but you should still be able to run the g++ compiler. That is all we need. If you really cannot log into the fedora machines, then just use GL to record your timing runs.
If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command:
Do remember to exit from the script command. This creates a file called typescript that will record any compilation errors. Yes, we know you can edit this file, but the compilation errors will just show up when we compile the programs again and you will still get lots of points deducted. This step is to compel you to fix any changes needed to get your program to compile on GL without any errors.
Note: cd to the appropriate directory if you are submitting late.
Now you can delete the executable files with
Then you should just have 7 files in your submission directory (the 6 source files plus the typescript). Check using the ls command. You can also double check that you are in the correct directory using the pwd command. (You should see your username instead of xxxxx.)
A Note on Timing
The main programs for timing above ( p2timetest1.cpp, p2timetest2.cpp and p2timetest3.cpp) double the number of items and the number of calls to SqList member functions each time. Since we expect the total running time to be O(n √n), doubling the value of n should increase the total running time by a factor of approximately 2.82. This is because
2n √ 2n = 2 √2 n √n
and 2 √2 ≈ 2.82. On some systems (e.g., Mac OS X), the running times bear this out:
The ratios 2.814/0.978 ≈ 2.877 and 8.201/2.814 ≈ 2.914 are quite close to the predicted value of 2.82.
However, it turns out that the Standard Template Library is not so standard. (See note on GNU website.) In particular the running time of the size() function may be O(1), which is what we want, or O(n), which is what is on GL. So, timing the same programs on GL gives quadratic running time.
Each successive run gives roughly quadruples the running time: 1.122/0.292 ≈ 3.84 and 4.248/1.122 ≈ 3.786. Your implementation should assume that size() takes O(1) time.