CMSC 341 Data Structures — Projects & Support — Spring 2020

Project 4: Skew Heap Priority Queue

Due: Tuesday, April 28, before 9:00 pm

---

Addenda

• If getNextJob() is called on an empty queue, it should throw a domain_error exception.
• The mergeWithQueue() function takes a single parameter: const JQueue& rhs. The description of the function says that rhs should be empty when the function finishes, which is not possible if it is defined const (well, it can be left empty, but you can't set _heap = nullptr, so you end up with memory problems). The function headers in in jqueue.h and jqueue.cpp have been updated, removing const. The original version are still available as jqueue_v0.h and jqueue_v0.cpp

---

Objectives

The objectives of this programming assignment are:

• Implement a skew heap, an advanced heap data structure.
• Gain additional experience constructing and using binary trees.
• Learn to use function pointers.
• More practice with recursion!

---

Introduction

Job Queues

On High Performance Computing (HPC) clusters, there is typically greater demand for compute resources than can be met at any one time. The job management system maintains a queue of submitted compute jobs and determines which jobs can be run based on policy set by the administrators. For example, a compute job that requires a small number of processors, say 16, and is expected to run for only a few minutes, might be prioritized ahead of a job that requires many processors and hours or days to run. On the other hand, there may be times (e.g. times of lower demand such as nighttime or over school breaks) where the resource-intensive jobs are given priority. Therefore, the job queue must be very flexible and able to support a wide range of prioritization functions.

In this project, you will implement a job queue class (JQueue) based on a max-skew heap data structure; it will maintain a max-skew heap based on the computed priority of each job, where the priority function is provided to the JQueue constructor via a function pointer. Inserting to and extracting from the skew uses a simple skew heap merge function which guarantees that the max-heap property is maintained; the comparisons that are part of the merge process will be made on the computed priorities of jobs in the skew heap. The class allows for the priority function to be changed, in which case the skew heap must be rebuilt.

For the purposes of this project, compute jobs have the following attributes (defined in jqueue.h) that can be used by the prioritization function:

• Job Name
  A descriptive name; not useful for prioritization.
• Priority
  A user-specified priority in the range 1–100. This should not be confused with the computed priority, which takes the user-specified priority and other job attributes into account.
• User
  A user id in the range 0–100. The computed priority may depend on the user id.
• Group
  A group id in the range 0–100. Groups could represent different research groups or funding sources.
• Proc
  The number of processors required by the job, in the range 1–255.
• Mem
  Memory requirements per processor in number of Mb. The range is 1–65536 (1 Mb - 64 Gb).
• Time
  Maximum wallclock time required, in seconds. The range is 1–172,800 (1 second - 48 hours).

A particularly simple prioritization function would be to just use the user-specified priority. However, the function can be much more complicated. The following function is implemented in the sample driver:

1. Let pri be the computed priority. Initialize pri to the user-specified priority.
2. If the user id is 7 or 23, add 300 to pri; otherwise, add 100 to pri.
3. If the group id is 0 or 11, add 200 to pri; otherwise, add 100 to pri.
4. Subtract the number of processors requested from pri.
5. Subtract 1/100 of the requested memory size from pri.
6. Subtract 1/3600 of the requested time from pri.
7. The computed priority is the integer value of pri.

Skew Heaps

A skew heap is a type of heap data structure that, like a standard max-heap, has efficient insert(), max(), and removeMax() operations, but also allows for efficient merging of heaps. Unlike a standard heap, it is not space-efficient to implement a skew heap in an array or vector &ldash; we will have to use a linked binary tree structure.

Your skew heap must satisfy the Max-heap Property: for any node \(w\) in the tree, the priority of \(w\) must be greater than the priorities of its two children. This property guarantees that the element with highest priority is always in the root node of the tree, and so reading the highest priority element is just a matter of accessing the data in the root node.

The special feature of a skew heap is the merge operation which combines two skew heaps into a single, valid skew heap. Let p1 and p2 be positions in two skew heaps (e.g. pointers to nodes). The merge operation is defined recursively:

• If p1 is Null, return p2; similarly, if p2 is Null, return p1.
• Assume that p1 has higher priority than p2; if not, swap, p1 and p2.
• Swap the left and right subtrees of p1.
• Recursively merge p2 and the left subtree of p1, replacing the left subtree of p1 with the result of the recursive merge.

The following figure shows two skew heaps (blue and green) and the result of merging the two. All the steps of the merge procedure are described below the figure.

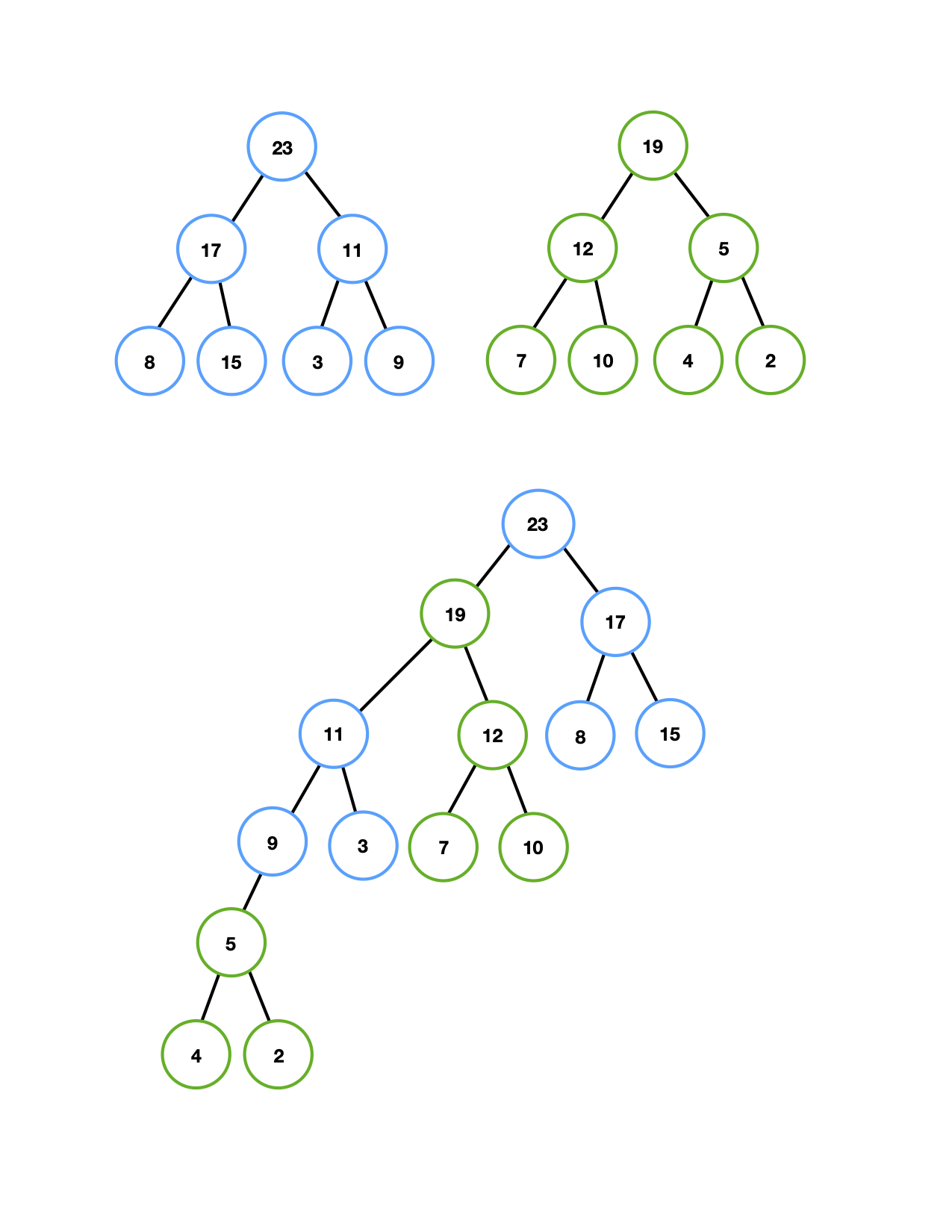
1. First Merge
   1. Make (23) the new root since 23 > 19.
   2. Swap (23)'s left and right subtrees.
   3. Recursively Merge (23)'s left subtree, which is the blue subtree rooted at (11), with the other skew heap; replace (23)'s left subtree with the merged subtree.
2. Second Merge
   Merge the green heap with the blue subtree rooted at (11).
   1. Make (19) the root since 19 > 11.
   2. Swap (19)'s left and right subtrees.
   3. Recursively Merge (19)'s left subtree (rooted at (5)) with the subtree rooted at (11); replace (19)'s left subtree with the merged tree.
3. Third Merge
   Merge the green subtree rooted at (5) with the blue subtree rooted at (11).
   1. Make (11) the root since 11 > 5.
   2. Swap (11)'s left and right subtrees.
   3. Recursively Merge (11)'s left subtree (the single node (9)) with the green subtree rooted at (5); replace (11)'s left subtree with the merged tree.
4. Fourth Merge
   Merge the green subtree rooted at (5) with the single node (9).
   1. Make (9) the root sinc 9 > 5.
   2. (9) has no children, so we don't have to swap anything.
   3. Recursively Merge (9)'s left subtree (which is empty!) with the green subtree rooted at (5); replace (9)'s left subtree with the merged tree.
5. Fifth Merge
   This is a trivial merge since one of the two trees is empty. We simply return the non-empty tree, which in this case is the green subtree rooted at (5).

Other Operations

The major operations supported by a max-skew heap are insertion of elements, reading the highest priority element, and removing the highest priority element. Reading the highest priority element is just a matter of reading the root node of the heap. The other two operations, insertion and removal, are applications of the merge function:

• To insert a new node x into an existing skew heap H, we treat x as a single-node skew heap and merge it with H.
• To remove the maximum priority value, we delete the root node and then merge the root's left and right sub-heaps.

We see, then, that the merge function is key to all of the major skew heap operations. If we can implement merge correctly, insertion and removal are simple.

Function Pointers

You're going to build a skew heap that can accepts a prioritization function from the user; this is accomplished by passing a function pointer to the constructor. The function pointer is the address of a function that will be used to compute the priority of a compute job. The function must take a job structure as input and return an integer priority.

A typedef for the function pointer is provided for you in jqueue.h:

typedef int (*prifn_t)(const job_t&);

This says that prifn_t is a pointer to a function that takes a job_t& argument. It must compute the priority from the contents of the job structure and return an integer. Sample priority functions and examples of their use are provided in the sample driver program.

---

Assignment

Your assignment is to complete the JQueue class, testing it thoroughly with a variety of job data and prioritization functions. To get started, you are provided with the following files:

• jqueue.h — declarations for the JQueue class.
• jqueue.cpp — JQueue implementation file. Empty except for overloaded insertion operators for the job and node structures.
• driver.cpp — a simple driver for the JQueue class.
• driver.txt — sample output from driver.cpp.

First, you must implement the methods of the JQueue class. The methods are described in the requirements section, below. Then, you must write your own, extensive test driver called mytest.cpp; your test driver should check at least the following properties of your JQueue implementation:

• Basic correctness. Creating a queue, inserting jobs, and reading them out in priority order functions correctly.
• Correctness of copy constructor, assignment operator.
• Can change the prioritization function using the setter method and the max-heap is rebuilt correctly.
• Efficiency with large queues. Insertion and extraction with a large queue operates in logarithmic time.

---

Specifications

These are the member functions of the jqueue class.

• JQueue(prifn_t priFn);

  This is the constructor for the JQueue class. It must be provided with a pointer to the prioritization function.

• ~JQueue();

  Destructor for the JQueue class. All dynamically-allocated data must be deallocated.

• JQueue(const JQueue& rhs);

  Copy constructor for the JQueue class. Must make a deep copy of the rhs object. Must function correctly if rhs is empty.

• JQueue& operator=(const JQueue& rhs);

  Assignment operator for the JQueue class. Remember to check for self-assignment and to free all dynamically allocated data members of the host. You should not use the copy constructor in the implementation of the assignment operator.

• void insertJob(const job_t input);

  Insert a job into the job queue. Must maintain the max-heap property.

• job_t getNextJob();

  Extract and return the highest priority job from the job queue. Must maintain the max-heap property. Should throw a domain_error exception if the queue is empty when the function is called.

• void mergeWithQueue(JQueue& rhs);

  Merge the host queue with the rhs; leaves rhs empty. Two skew heaps can only be merged if they have the same priority function. If the user attempts to merge queues with different priority functions, a domain_error exception should be thrown.

• void clear();

  Clear the job queue. Must delete all the nodes in the skew heap, leaving the skew heap empty.

• int numJobs() const;

  Return the current number of jobs in the queue.

• void printJobQueue() const;

  Print the contents of the queue using preorder traversal. Although the first job printed should have the highest priority, the remaining jobs will not necessarily be in priority order.

• prifn_t getPriorityFn() const;

  Get the current priority function.

• void setPriorityFn(prifn_t priFn);

  Set a new priority function. Must rebuild the heap!

• void dump() const;

  Use an inorder traversal to dump the heap an indicate the tree structure (as in the previous project). Represent a node in the tree by its integer priority as computed using the priority function.

---

Additional Requirements

Requirement: Private helper functions must be declared in jqueue.h. No other modifications to jqueue.h are permitted!

Requirement: You must use a max-skew heap data structure to store the job queue. The skew heap must be ordered according to the prioritization function priority declared in jqueue.h and set by the constructor or setter method. If the prioritization function is changed using the setter method, then the max-heap must be rebuilt using the new prioritization function.

Requirement: Computed priority values may not be pre-computed and stored with the jobs in the queue. They must be computed as needed using the priority function.

Requirement: Insertion to and extraction from the max-heap must run in amortized logarithmic time.

Requirement: You must use the provided operator<< to output job_t and Node objects.

---

What to Submit

You must submit the following files to the proj4 directory.

• jqueue.h
• jqueue.cpp
• mytest.cpp

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.

cp jqueue.h jqueue.cpp mytest.cpp ~/cs341proj/proj4/