Project 3: Chestnut Trees

Due: Tuesday, April 9, before 9:00 pm

Addenda

Objectives

The objectives of this programming assignment are:

Introduction

With AVL trees and Red-Black Trees, we maintain a balance condition to guarantee that the tree has O(log n) height. Are there other balance conditions that we can use to efficiently maintain a balanced tree?

In in a Chestnut Tree (CTree), a node is imbalanced if the difference of the sizes of the left and right subtrees exceeds two. We call this the size-balance property (analagous to the height-balance property for AVL trees). Insertion and deletion proceed as for an unbalanced binary search tree until we notice that the balance condition is violated; then we must rebalance the subtree of the CTree rooted at this node.

There is one method that we can always use to rebalance a subtree of a CTree: convert the entire subtree into a sorted array and then convert the array back into a perfectly balanced BST. Rebuilding is easy because the array is sorted. We can find the middle element of the array in constant time and make it the root of the new subtree. Then, we recursively build the left subtree and the right subtree using, respectively, the portion of the array that has keys smaller than the root and the portion of the array that has keys larger than the root. The result is a binary search tree that is as balanced as possible. (See Project 3 Examples.) The rebalance procedure takes O(t) on a BST subtree with t elements, so it is relatively inefficient. However, we don't have to rebalance very often.

Note: It is possible for a CTree to be imbalanced at two nodes x and y where x is an ancestor of y. In this situation, rebalance at x since this will also rebalance the subtree rooted at y. If you rebalance at y first, the time spent rebalancing at y is completely wasted since all that work is undone when you rebalance at x. (See Project 3 Examples.)

Is this really the best we can do to rebalance a CTree? Is there any way that we can used trinode restructuring from AVL trees? Unfortunately, there is no simple relationship between height-balanced and size-balanced BSTs: you can construct examples of BSTs that are height-balanced but not size-balanced, and vice versa. Nonetheless, there are some circumstances in which a trinode restructuring can be used to rebalance a CTree. (See Project 3 Examples for one example.)

Assignment

Your assignment is to implement a CTree. The high-level requirements and points distribution are as follows:

  1. [80 points] A correct and efficient implementation of CTree implementing the basic, array-based restructuring method. Full credit requires appropriate use of recursion and adherence to coding standards.
  2. [10 points] Analysis of special cases in which trinode restructuring could be applied for faster rebalancing; implementation of trinode restructuring for one or more of these cases.
  3. [10 points] A of the special cases from (2). Type your answers in the provided text file and submit it along with your code.

Since you will choose the design of the class definitions, no header files will be distributed with this project. Instead, the requirements are:

In order to implement CTree efficiently, your data structure must be able to determine the size and height of a subtree in constant time. You must have data members for the height and size of a subtree in the class representing the root of a subtree of a CTree. The height and size data members must be updated whenever the height or size of that subtree changes. The update must not affect the asymptotic running time of insert, delete and search. These must still run in time proportional to the height of the tree.

To keep things simple for this project, we will just store int values in CTree. Although, well-written code should allow you to easily change the type of data stored in the data structure.

Here are the member functions you must implement in your CTree class. You will need to implement others for your own coding needs.

  1. A default constructor with the signature 

       CTree::CTree() ;

    The default constructor must create a CTree object that is ready to have its member function invoked without any further processing.

  2. A copy constructor with the signature 

       CTree::CTree(const CTree& other) ;

    The copy constructor must make a deep copy and create a new object that has its own allocated memory.

  3. A destructor with the signature 

       CTree::~CTree() ;

    The destructor must completely free all memory allocated for the object. (Use valgrind on GL to check for memory leaks.)

  4. An overloaded assignment operator with the signature: 

       const CTree& CTree::operator=(const CTree& rhs) ;

    The assignment operator must deallocate memory used by the host object and then make deep copy of rhs.

  5. An insert() function that adds an item to CTree that has the following signature: 

       void CTree::insert (int key) ;

    The insert() function must run in time proportional to the height of the CTree, not counting time for rebalancing. Your CTree implementation must not allow duplicates. If the insert() function is invoked with a key value that already stored in the CTree, your insert() function should do nothing, except that it may rebalance the tree if an imbalance is detected.

  6. A remove() member function that finds and removes an item with the given key value. The remove() function should return a boolean value that indicates whether the key was found. Your remove() function should not abort or throw an exception when the key is not stored in the BST. The remove() member function must have the following signature: 

       bool CTree::remove(int key) ;

    For full credit, your remove() method must run in time proportional to the height of the tree, not counting time for rebalancing.

  7. A find() function that reports whether the given key is stored in the tree. The signature of the find() method should be: 

       bool CTree::find(int key) ;

    For full credit, your find() method must run in time proportional to the height of the tree.

  8. A member function rebalance() that rebalances a subtree of the CTree as described above. The running time of rebalance() must be proportional to the number of nodes in the subtree being rebalanced. Note that a proper implementation would require you the keep track of the size and height of the subtree. Read the description above.

  9. A member function inorder() that performs an inorder walk of the CTree and at each node, prints out the key followed by a : followed by the height of the node followed by another : followed by the size of the subtree rooted at that node. Furthermore, inorder() should print an open parenthesis before visiting the left subtree and a close parenthesis after visiting the right subtree. Nothing should be printed when inorder() is called on an empty tree, not even parentheses. This function will be used for grading, so make sure that it works correctly. The function must have the following signature: 

       void CTree::inorder() ;

    For example, calling inorder() on the following BST should produce the string:

    (((((3:0:1)7:2:4((9:0:1)11:1:2))14:3:8((15:1:2(17:0:1))20:2:3))22:4:13 (((24:0:1)26:1:2)30:2:4(37:0:1)))41:5:22((((50:0:1)54:1:3(59:0:1))60:2:4) 64:3:8((71:1:2(75:0:1))79:2:3)))

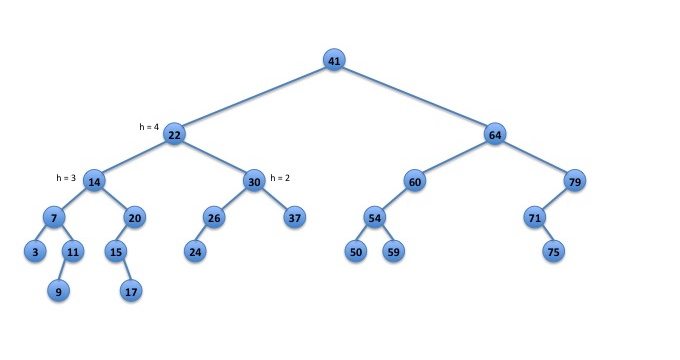
    Fig. 1: An unbalanced binary search tree.

    Here, the 41:5:22 indicates that the node with key 41 has height 5 and that there are 22 nodes in the tree. The output before 41:5:22 is produced by visiting the left subtree. Everything after 41:5:22 is produced by visiting the right subtree.

  10. A function locate() that returns whether there is a node in a position of the CTree and stores the key in the reference parameter. The position is given by a constant C string, where a character 'L' indicates left and a character 'R' indicates right. The locate() function must have the signature 

       bool CTree::locate(const char *position, int& key) ;

    For example in the BST above:
    • A call to locate("LRL",key) should return true and store 26 in key.
    • A call to locate("RRLR",key) should return true and store 75 in key.
    • A call to locate("RLR",key) should return false and not make any changes to key since there is not a node in that position.
      Note: locate() must not abort and must not throw an exception in this situation.
    • A call to locate("",key) should return true and store 41 in key, since the empty string indicates the root of tree.

    The grading programs will use locate() to check if your BST is balanced and that the keys are stored correctly. So, make sure locate() is correct.

Your code must run without segmentation fault and without memory leaks. For grading purposes, memory leaks are considered as bad as segmentation faults. This is because many segmentation faults are caused by poorly written destructors. A program with an empty destructor might avoid some segmentation faults but will leak memory horribly. Thus, not implementing a destructor or not deleting unused memory must incur a penalty similar to that of a segmentation fault.

Test Programs

Some sample driver programs to test your implementation are provided below. Passing these tests does not mean you will receive an 'A' on your project. It does not guarantee that you will pass tests used in grading. You should construct additional tests of your own!

Note: your output may differ from the sample out provided as there are various correct implementations of remove() and rebalance().

Implementation Notes

What to Submit

You must submit the following files to the proj3 directory.

The Driver.cpp program should include tests showing the parts of your project that work correctly.

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.

cp CTree.h CTree.cpp Driver.cpp analysis.txt ~/cs341proj/proj3/

Note: The written analysis in analysis.txt is optional. See the general requirements in the Assignment section.