Project 3: CTree Examples
Figure 1 shows an example of an unbalanced binary search tree. At node 22, the left subtree has 8 nodes and the right subtree only has 4 nodes. If we encountered node 22 during an insert, we would invoke rebalance() on the subtree rooted at node 22.
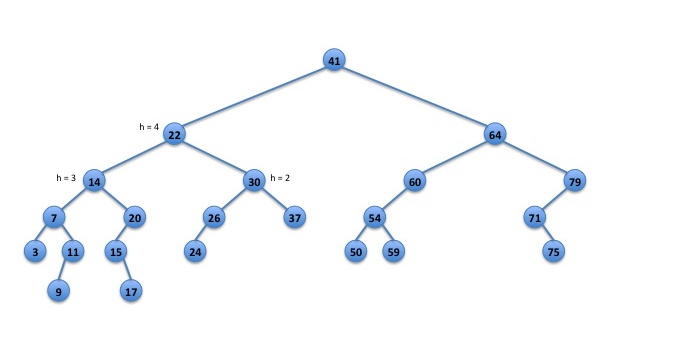
Fig. 1: An unbalanced binary search tree.
After the first step of the rebalance() procedure, the left subtree of node 41 has been converted into an array, as shown in Figure 2, below:
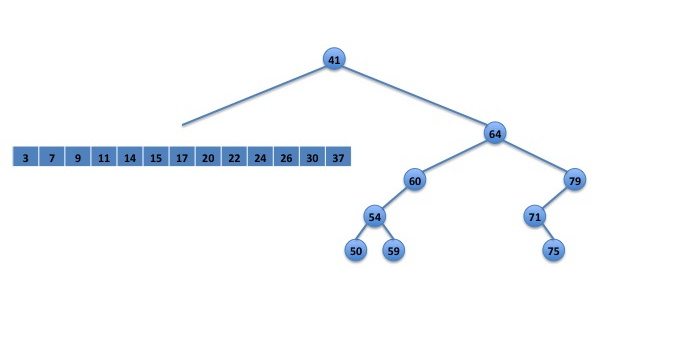
Fig. 2: Subtree converted to an array.
When we rebuild the BST, we pick the middle element of the array, 17 in this case, and make it the root of the new subtree.
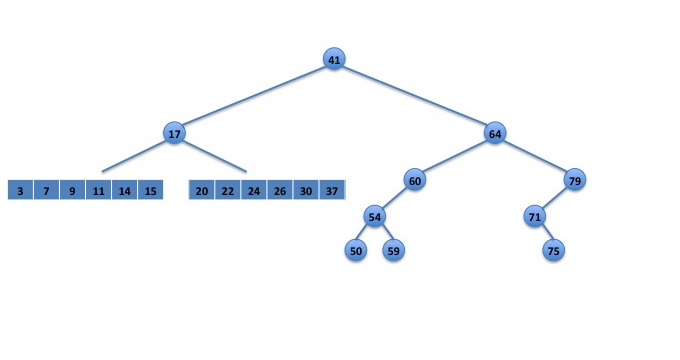
Fig. 3: 17 chosen as the root of the new subtree.
Items smaller than 17 are used to rebuild the left subtree of node 17. The items larger than 17 are used to rebuild the right subtree of node 17. The result is a BST that is as balanced as possible:
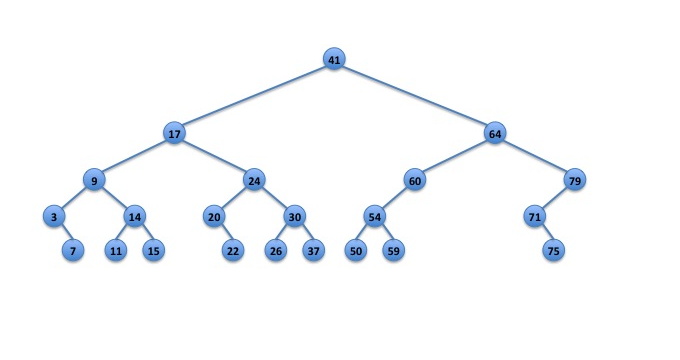
Fig. 4: Array converted back to a BST.
Note, however, that node 41 is also imbalanced with 13 nodes in the left subtree and 8 in the right subtree. In this case, it would have been better to restructure at node 41, correcting the imbalances at node 41 and node 22 with a single restructuring.
Another Example
In Figure 5, there are several imbalanced nodes: 20, 22, 60, and 41. As with the first example, it would be best to restructure at node 41, which will correct all the imbalanced nodes.
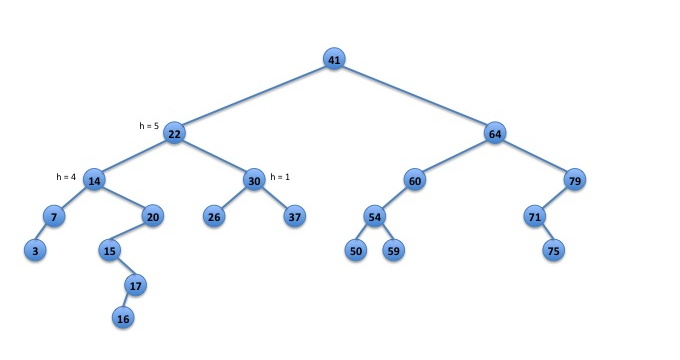
Fig. 5: An unbalanced binary search tree.
Trinode Restructure Example
Figure 6 shows a tree that, after insertion of node 3, is both height- and size-imbalanced at the root. In this case, a trinode restructure will fix the size-imbalance.
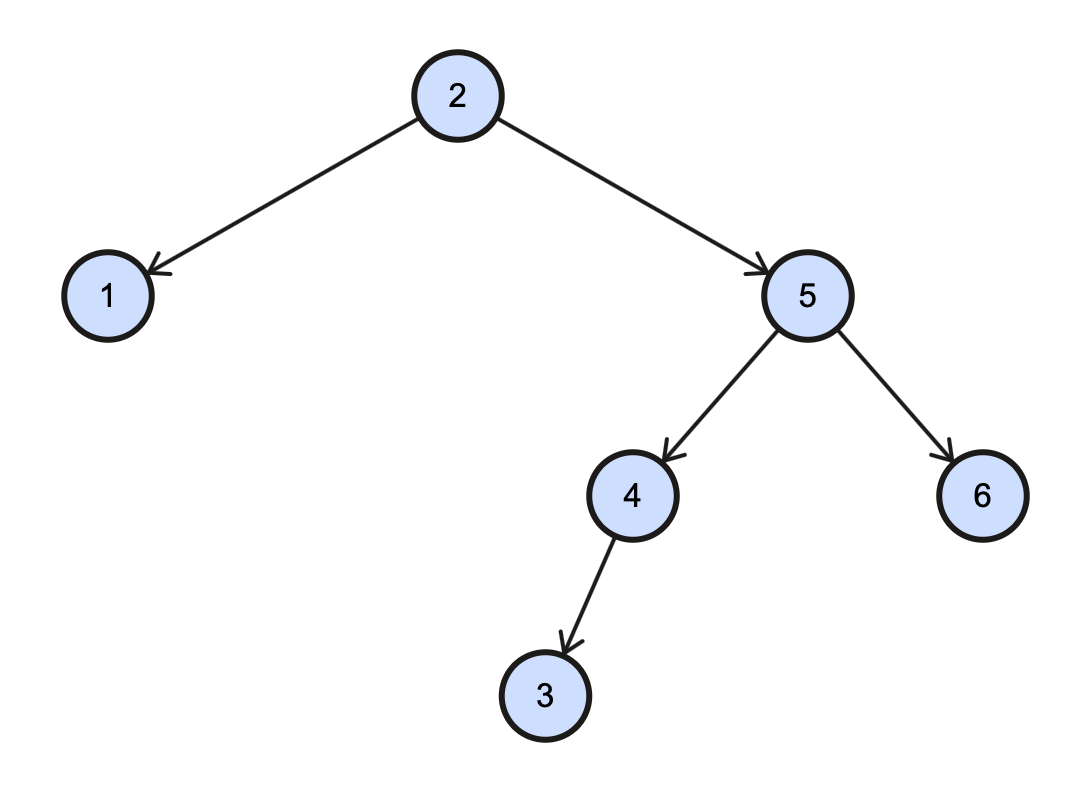
Fig. 6: Height- and size-imbalanced tree
Following the trinode restructure procedure, we would label node 2 as z, node 5 as y, and node 4 as x; the inorder listing would lable node 2 as a, node 4 as b, and node 5 as c. Then b becomes the new root, replacing z, a becomes the left child of b, b's left child becomes the right child of a, and c becomes the right child of b. The result is shown in Figure 7.
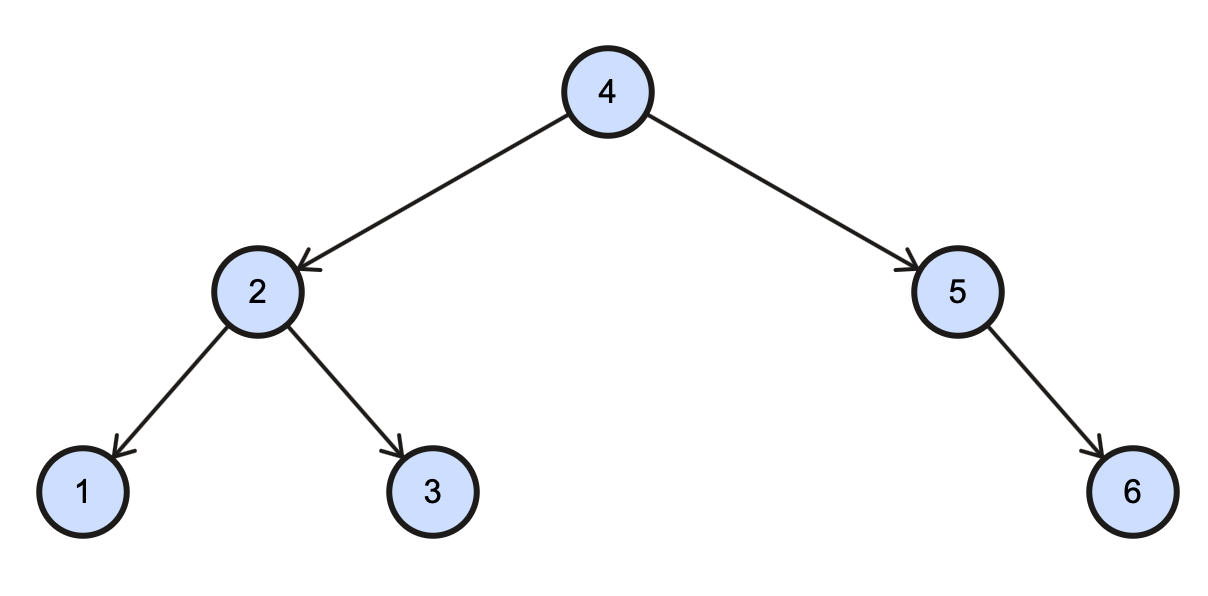
Fig. 6: Tree after trinode restructure
The trinode restructure runs in constant time, compared with O(t) for the array-based restructuring procedure (here t is the size of the subtree being restructured).