Thomas A. Anastasio
9 February 2000
As a programmer, you often have a choice of data structures and algorithms. Choosing the best one for a particular job involves, among other factors, two important measures:
You will sometimes seek a tradeoff between space and time complexity. For example, you might choose a data structure that requires a lot of storage in order to reduce the computation time. There is an element of art in making such tradeoffs, but you must make the choice from an informed point of view. You must have some verifiable basis on which to make the selection of a data structure or algorithm. Complexity analysis provides one such basis.
We would like to have a way of describing the inherent complexity of a program (or piece of a program), independent of machine/compiler considerations. This means that we must not try to describe the absolute time or storage needed. We must instead concentrate on a ``proportionality'' approach, expressing the complexity in terms of its relationship to some known function. This type of analysis is known as asymptotic analysis.
Speaking very roughly, ``Big Oh'' relates to an upper bound on complexity, ``Big Omega'' relates to a lower bound, and ``Big Theta'' relates to a tight bound. While the ``bound'' idea may help us develop an intuitive understanding of complexity, we really need formal and mathematically rigorous definitions. You will see that having such definitions will make working with complexity much easier. Besides, the ``bounds'' terminology is really not quite correct; it's just a handy mnemonic device for those who know what asymptotic analysis is really about.
![]() Definition:
Definition:
![]() if and only if there are constants
if and only if there are constants
![]() and
and ![]() such that
such that
![]() for all
for all ![]() .
.
The expression
![]() is read as ``T of n is in BigOh of f of
n,'' or ``T of n is in the set BigOh of f of n,'' or ``T of n is
BigOh of f of n.''
is read as ``T of n is in BigOh of f of
n,'' or ``T of n is in the set BigOh of f of n,'' or ``T of n is
BigOh of f of n.''
The definition may seem a bit daunting at first, but it's really just
a mathematical statement of the idea that eventually ![]() becomes
proportional to
becomes
proportional to ![]() . The ``eventually'' part is captured by
``
. The ``eventually'' part is captured by
``![]() ;''
;'' ![]() must be ``big enough'' for
must be ``big enough'' for ![]() to have settled
into its asymptotic growth rate. The ``proportionality'' part is
captured by
to have settled
into its asymptotic growth rate. The ``proportionality'' part is
captured by ![]() , the constant of proportionality.1
, the constant of proportionality.1
The definition is ``if and only if.'' If you can find the constants
![]() and
and ![]() such that
such that
![]() , then
, then
![]() .
Also, if
.
Also, if
![]() , then there are such constants. It works
both ways.
It may be helpful to recognize that
, then there are such constants. It works
both ways.
It may be helpful to recognize that ![]() is a set. It's the set
of all functions for which the constants exist and the inequality
holds.
is a set. It's the set
of all functions for which the constants exist and the inequality
holds.
If a function
![]() , then eventually the value
, then eventually the value ![]() will
exceed the value of
will
exceed the value of ![]() . ``Eventually'' means ``after
. ``Eventually'' means ``after ![]() exceeds some value.'' Does this really mean anything useful? We might
say (correctly) that
exceeds some value.'' Does this really mean anything useful? We might
say (correctly) that
![]() , but we don't get a lot of
information from that;
, but we don't get a lot of
information from that; ![]() is simply too big. When we use BigOh
analysis, we implicitly agree that the function
is simply too big. When we use BigOh
analysis, we implicitly agree that the function ![]() we choose is
the smallest one which still satisfies the definition. It is correct
and meaningful to say
we choose is
the smallest one which still satisfies the definition. It is correct
and meaningful to say
![]() ; this tells us
something about the growth pattern of the function
; this tells us
something about the growth pattern of the function ![]() , namely
that the
, namely
that the ![]() term will dominate the growth as
term will dominate the growth as ![]() increases.
increases.
While BigOh relates to upper bounds on growth, BigOmega relates to lower bounds. The definitions are similar, differing only in the direction of the inequality.
![]() Definition:
Definition:
![]() if and only if there are constants
if and only if there are constants
![]() and
and ![]() such that
such that
![]() for all
for all ![]() .
.
In this case, the function ![]() is proportional to
is proportional to ![]() when
when ![]() is big enough, but the bound is from below, not above.
As with BigOh, the expression
is big enough, but the bound is from below, not above.
As with BigOh, the expression
![]() is read as ``T of
n is BigOmega of f of n,'' or ``T of n is in BigOmega of f of n,'' or
``T of n is in the set BigOmega of f of n.''
is read as ``T of
n is BigOmega of f of n,'' or ``T of n is in BigOmega of f of n,'' or
``T of n is in the set BigOmega of f of n.''
![]() , like
, like ![]() , is the set of functions for which the
constants exist and the inequality holds.
, is the set of functions for which the
constants exist and the inequality holds.
Finally, we define BigTheta. It is defined in terms of BigOh and BigOmega. A function is in BigTheta if it's both in BigOh and in BigOmega.
![]() Definition:
Definition:
![]() if and only if
if and only if
![]() and
also
and
also
![]() .
.
Intuitively this means that ![]() forms both an upper- and
lower-bound on the function
forms both an upper- and
lower-bound on the function ![]() ; it is a ``tight'' bound.
; it is a ``tight'' bound.
The following functions are often encountered in computer science complexity analysis. We'll express them in terms of BigOh just to be specific. They apply equally to BigOmega and BigTheta.
A[i] takes the same number of
steps no matter how big A is.
The growth patterns above have been listed in order of increasing
``size.'' That is,
The best case for an algorithm is that property of the data that results in the algorithm performing as well as it can. The worst case is that property of the data that results in the algorithm performing as poorly as possible. The average case is determined by averaging algorithm performance over all possible data sets. It is often very difficult to define the average data set.
Note that the worst case and best case do not correspond to upper
bound and lower bound. A complete description of the complexity of an
algorithm might be ``the time to execute this algorithm is in ![]() in the average case.'' Both the complexity and the property of the
data must be stated. A famous example of this is given by the
quicksort algorithm for sorting an array of data. Quicksort is in
in the average case.'' Both the complexity and the property of the
data must be stated. A famous example of this is given by the
quicksort algorithm for sorting an array of data. Quicksort is in
![]() worst case, but is in
worst case, but is in ![]() best and average cases.
The worst case for quicksort occurs when the array is already sorted
( i.e., the data have the property of being sorted).
best and average cases.
The worst case for quicksort occurs when the array is already sorted
( i.e., the data have the property of being sorted).
One of the all-time great theoretical results of computer science is
that any sorting algorithm that uses comparisons must take at least
![]() steps. That means that any such sorting algorithm,
including quicksort, must be in
steps. That means that any such sorting algorithm,
including quicksort, must be in
![]() . Since quicksort
is in
. Since quicksort
is in ![]() in best and average cases, and also in
in best and average cases, and also in
![]() , it must be in
, it must be in
![]() in best and average
cases.
in best and average
cases.
enqueue operation requires traversing the entire list to find
the end, then ``attaching'' the new item at the end. What is the
asymptotic time complexity of this operation as a function of enqueue operation has
asymptotic complexity enqueue
You may object that the list is not ![]() long until all
long until all ![]() items have
been enqueued. Look at it this way; the first item takes one
operation, the second takes two operations, the third takes three
operations, etc. Therefore, the total number of operations to
items have
been enqueued. Look at it this way; the first item takes one
operation, the second takes two operations, the third takes three
operations, etc. Therefore, the total number of operations to
enqueue ![]() items is
items is
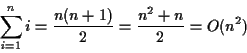
A better implementation would provide ![]() performance for each
performance for each
enqueue operation, thereby allowing ![]() items to be
items to be
enqueued in ![]() time. This is significantly better than
time. This is significantly better than
![]() (check the chart for
(check the chart for ![]() , for instance).
, for instance).
![]()
![]() Proof:
Proof:
![]() implies that there are constants
implies that there are constants ![]() and
and ![]() such that
such that
![]() when
when ![]()
Therefore,
![]() when
when ![]() where
where ![]()
Therefore,
![]()
![]()
![]()
![]() Proof: From the definition of Big Oh,
Proof: From the definition of Big Oh,
![]() for
for ![]() and
and
![]() for
for ![]()
Let
![]()
Then, for ![]() ,
,
![]()
Let
![]()
Then
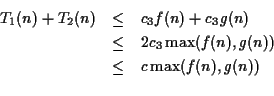
![]()
![]() Proof:
Proof:
![]() is a polynomial of degree
is a polynomial of degree ![]()
By the sum rule (Theorem ![[*]](cross_ref_motif.gif) ), the largest term dominates.
), the largest term dominates.
Therefore, ![]()
![]()
As an example, it can be shown that in BubbleSort, SelectionSort, and
InsertionSort, the worst case number of comparisons is
![]() . What is
. What is
![]() ?
Well,
?
Well,
![]() which is a polynomial.
Since constants don't matter (Theorem
which is a polynomial.
Since constants don't matter (Theorem ![[*]](cross_ref_motif.gif) ),
),
![]() .
By the sum rule (Theorem
.
By the sum rule (Theorem ![[*]](cross_ref_motif.gif) ),
),
![]() .
.
The proofs of Theorems ![[*]](cross_ref_motif.gif) and
and ![[*]](cross_ref_motif.gif) , below, use
L'Hospital's rule. Recall that this rule pertains to finding the
limit of a ratio of two functions as the independent variable
approaches some value. When the limit is infinity, the rule states that
, below, use
L'Hospital's rule. Recall that this rule pertains to finding the
limit of a ratio of two functions as the independent variable
approaches some value. When the limit is infinity, the rule states that
We use L'Hospital's rule to determine ![]() or
or ![]() ordering of
two functions.
ordering of
two functions.
![]()
![]() Proof: Note that
Proof: Note that ![]() means
means ![]()
We must show
![]() for
for ![]() . Equivalently, we can
show
. Equivalently, we can
show
![]() . Letting
. Letting
![]() , we will
show that
, we will
show that
![]() , for any positive constant
, for any positive constant ![]() . Use
L'Hospital's rule:
. Use
L'Hospital's rule:
As a really outrageous (but true) example,
![]() .
. ![]() grows very slowly!
grows very slowly!
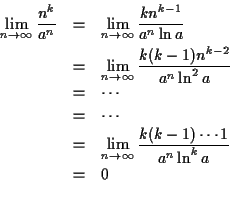
As a really outrageous (but true) example,
![]() . Exponentials grow very rapidly!
. Exponentials grow very rapidly!
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 asymptotic.tex
The translation was initiated by Thomas Anastasio on 2000-02-09