IFSM 300 – Class 5

February 11, 2002 

Preliminaries

·        Return homework 1.

·        Class Web site reminder: http://www.gl.umbc.edu/~rrobinso/

·        Assignment 5: for the next class, read chapter 5.

·        Homework 2 (in assignment 5): due Monday, February 18. 

Introduction to Bayesian Methods

·        Now we consider two different subjects, which may cause confusion if not separated.

·        First, when we gain new information pertinent to probabilities, how do we revise the probabilities we had originally? This is achieved by applying the definition of conditional probability, which may be rewritten algebraically into a form called Bayes’ Theorem.

·        Second, we use the same procedures to combine information pertinent to probabilities from two sources – historical data (leading to objective probabilities) and personal judgement (leading to subjective probabilities).

·        It’s not obvious that the usual mathematics of objective probabilities should be applied to subjective probabilities. For example, you might argue that personal judgements are shaky and should be revised more than objective probabilities in the event some objective data comes along. That treating them the same makes sense (and it does) is another cornerstone of DA.  

Decision Trees With Revising of Probabilities (Part 1)

·        Refer to New Product Marketing, situation 5.1, page 164.

·        Complete notes below. Summary here.

·        Draw the decision tree for Table 5.1, page 165.

·        Review sensitivity graph in Figure 5.1, page 167.

·        Calculate and interpret EV*, EVC, and EVPI. 

Decision Trees With Revising of Probabilities (Part 2)

Introduction Today, Continuing in Lecture 6

·        See notes below for topics covered in this class. 

Millionaire Q1

To revise probabilities with new information, we use:

A.     The same procedure we use to combine objective and subjective probabilities.

B.     The definition of conditional probability.

C.     Bayes’ Theorem.

D.    Any of the above.(!!) 

Millionaire Q2

The method (not covered in our book) by which DA balances expected gain against risk is:

A.     Utility theory. (!!)

B.     Theory of probability.

C.     Random walk theory.

D.    Risk-reward theory. 

Millionaire Q3

An analysis to show how much the recommended decision in a DA varies as we vary the values of inputs is called:

A.     Variation analysis.

B.     Stability analysis.

C.     Sensitivity analysis. (!!)

D.    Fluctuation analysis. 

Millionaire Q4

The maximum amount we should be willing to pay for information that removes all uncertainty is called:

A.     Expected value under uncertainty.

B.     Expected value under certainty.

C.     Expected value of imperfect information.

D.    Expected value of perfect information. (!!) 

Millionaire Q5

The probability that events A and B will happen together (that is, both A and B will happen) is called:

A.     Combined probability of A and B.

B.  Shared probability of A and B.

C.  Co-probability of A and B.

D.  Joint probability of A and B. (!!)

 Millionaire Q6

Bayes’ Theorem is an algebraic rewriting of:

A.     The definition of joint probability.

B.     The definition of marginal probability.

C.     The definition of conditional probability. (!!)

D.    The definition of fuzzy probability. 

Complete Notes

·        On the pages that follow.
 

Notes: Decision Trees with Revising of Probabilities (Part 1)

New Product Marketing

Example. We begin by analyzing the following problem, from pages 164 and 165: 

Situation 5.1 New Product Marketing 

Pucter and Simple is a consumer household goods manufacturer that wants to consider the introduction of a new toothpaste. The new product, which will be labeled Brite, could replace a relatively low-profit existing brand called Kist. Product profits would depend on sales volume, which could be low or high. The situation is depicted by Table 5.1, where entries represent potential profits. Based on available current data and experience with similar products, management believes there is a 45 percent chance of low sales. The company wants to select the alternative that results in the maximum expected profit.

            Table 5.1 Potential Profits

Decision Tree. The complete decision tree for this example is single-stage – one decision followed by uncertain outcomes that determine the payoffs:

Utility Revisited. Observe that action a₁ (market Brite), while it offers a higher EV, is more risky. That is, the possible profit outcomes for a₁ are spread more widely than for a_2;  moreover, we could lose 500 with a₁ while a₂ presents no chance of loss.  

To address this, we use the method called utility -- not covered in our book but reviewed briefly in the lecture of class 4. Utility enables us to adjust the profit values in the decision tree, keeping all solution procedures otherwise the same, so that the client’s personal attitude toward risk will determine whether or not to select a₁ despite its extra riskiness. 

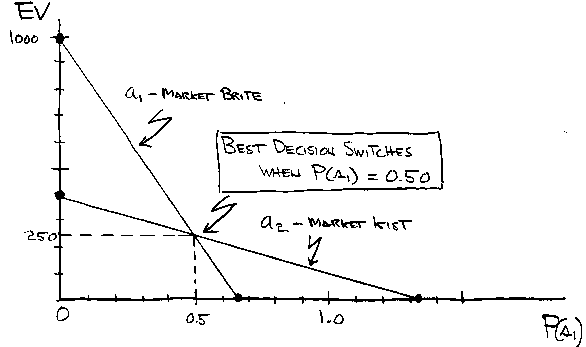
Sensitivity Analysis.  Question: How much would we have to revise our estimate of the probability P(s₁) before the analytically best decision changes from a₁ to a₂? If the answer is “Not much.”, we should study P(s₁) further to sharpen our estimate of its value. 

Because the EVs of  a₁ and a₂ depend, in this extremely simple example, only on P(s₁) rather than on several probabilities, we can plot a graph that shows the full story. On the graph we place one EV-versus-P(s₁) curve for choice a₁, a second EV-versus-P(s₁) curve for choice a₂. Where the two curves cross indicates what P(s₁) switches the best choice from a₁ to a₂.

To determine how to plot the curves on the graph, refer to the decision tree. Focus on choice a₁ (market Brite). Note that the EV of a₁ (call it EV₁) is P(s₁) times the profit –500 plus P(s₂) times the profit +1,000. We can write this relationship, substitute [1 – P(s₁)] for P(s₂), and simplify to obtain the equation of the curve:

EV₁ = - 500 P(s₁) + 1,000 P(s₂)

       = - 500 P(s₁) + 1,000 [1 – P(s₁)]

       = - 500 P(s₁) + 1,000 – 1,000 P(s₁)

EV₁ = 1,000 – 1,500 P(s₁). 

This is the equation of a straight line. To plot the corresponding line, we want to find the intercepts. Let P(s₁) be 0 and solve for the EV intercept; then let EV be 0 and solve for the P(s₁) intercept: 

P(s₁) = 0, EV = 1,000, which, stated in the form (x,y), is (0, 1000)

EV = 0, P(s₁) = 1000/1500 = 0.67, or                                (0.67, 0). 

Repeating this procedure for choice a₂ (market Kist), we find the equation of the line and then its intercepts: 

EV₂ = 100 P(s₁) + 400 [1 – P(s₁)]

       = 100 P(s₁) + 400 – 400 P(s₁)

EV2 = 400 – 300 P(s₁) 

Intercepts (0, 400) and (1.33, 0). 

By plotting both lines, we can see that the best choice (the higher EV) comes from a₁ when the value of P(s₁) is smaller than the value where the lines cross, and the best choice is a₂ when P(s₁) is larger than the crossover value.

From the graph, we could estimate the crossover value of P(s₁). But to get an exact value, we use the equations above and the fact that at crossover EV₁ = EV₂:

1000 – 1500 P(s₁) = 400 – 300 P(s₁)

           1000 – 400 = 1500 P(s₁) – 300 P(s₁)

                       600 = 1200 P(s₁)

                     P(s₁) = 600/1200 = 0.5

                        EV = 400 – 300 (0.5) = 250

Crossover point is (0.5, 250). 

Where We Are Headed. The conclusion we probably would reach from the sensitivity analysis just reviewed is that our current estimate P(s₁) = 0.45 is quite close to that critical value P(s₁) = 0.50 where the analytically best decision would change from a₁ to a₂. So we may well wish to sharpen our estimate of P(s₁).  

To do that, we could buy market research. Should we in fact buy the market research that’s available to us? In what follows, we’ll see how Bayesian methods enable us to answer that question. 

Expected Value Under Certainty. What is the most we should pay for market research? We’ll assess later whether it seems worthwhile to pay the price of market research that actually is available. Meanwhile, we can quickly estimate the maximum amount we ever would consider paying by calculating what perfect research would be worth. 

Real-world imperfect research would permit us to sharpen our P(s₁) but still leave us with some uncertainty. Hypothetical perfect research, in contrast, would remove uncertainty by telling us P(s₁) = 1.0 or P(s₁) = 0.

The general idea we shall put to work here is that the worth of perfect research is the amount by which the expected profit would improve if we in fact had perfect research. The procedure turns out to be simple. Yet the reasoning is slippery, and thus deserves careful attention.  

Our first step is to calculate the expected value under certainty, symbol EVC. The concept is to recalculate the EV* (= $325,000) of our original tree-diagram analysis, assuming now that we have hypothetical “perfect” market research, giving us the “perfect information” that removes uncertainty. We’ll first review how to do this, and then go over the reasoning.

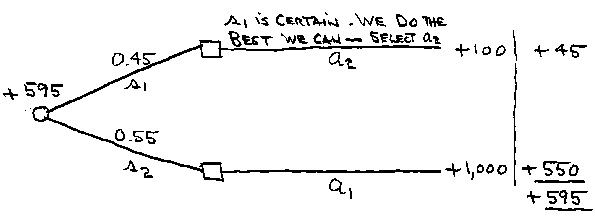
Draw a special tree diagram in which you reverse the usual order --  in this diagram, the chance node comes first:

EVC = $595,000                          s₂ is certain. We do the

   best we can – select a₁ 

In this special tree diagram, the basic idea is to choose the best action after you learn whether demand will be low (s₁) or high (s₂). In the original decision tree, for instance, you can see that if we had low demand s₁ we would get a profit of –500 from selecting a₁ but + 100 from selecting a₂. So the best action given s₁ is certain is a₂ with profit +100.  

In other words, you imagine you are consulting a forecaster who has a “crystal ball.”  The forecaster tells you that s₁ will happen. Knowing now that s₁ will happen, you then select the best action: a₂. 

Here’s the slippery part. Why are we calculating an expected value if we assume no future uncertainty? The answer is that we are making an assessment now, before obtaining the perfect information (before going to see the forecaster with the crystal ball). We don’t know at this time what the perfect information will be (what the forecaster will tell us). But we do know the probabilities of s₁ and s₂. Thus, we believe that P(s₁) is the probability the perfect information will be that s₁ will occur (the forecaster will say s₁). And we believe P(s₂) is the probability the perfect information will be that s₂ will occur (the forecaster will say s₂). Using those probabilities, we calculate the expected value now of the profit that would come from our taking the best action later, after we obtain the perfect information (after we learn what the forecaster says).

Expected Value of Perfect Information. Once we have calculated EVC, the next step is to calculate the expected value of perfect information, symbol EVPI. The EVPI shows the most that we ever would pay for information to sharpen the probability estimates. It’s the amount by which our EV* could improve if the information we plan to purchase would remove all uncertainty: 

EVPI º ½EVC – EV*½ = ½595 - 325½ = 270 = $270,000. 

The symbol  “º” means “is defined to be.” The vertical lines “½…½” mean “absolute value,”  indicating that we treat the result as positive whether or not EVC is larger than EV*. We want the absolute value because EV* will be larger than EVC with payoffs (like cost) that we minimize.

Notes: Decision Trees with Revising of Probabilities (Part 2)

Marketing Research

Conditional and Joint Probabilities. Before continuing to discuss the question of whether or not to purchase market research in the Brite-and-Kist example, we must review more about probability. 

Suppose you have two different wheels of fortune. One wheel contains 2 red spokes and 3 blue spokes, for a total of 5 equally likely spokes. The second wheel contains 4 red spokes and 1 blue spoke, for a total of 5 equally likely spokes.  

Imagine an experiment in which you first toss a fair coin and then select a wheel of fortune to spin:

A complete probability tree for this experiment is:         

Note that the probability 2/5 for red after heads is not the overall probability of red, because red also may occur after tails. Rather, 2/5 is the probability of red given that heads happened. The notation for this conditional probability is P(R½H), where the vertical line means given or assuming.

The symbol Ç (cap or intersection) represents together. So HÇR means we got heads and then red, a so-called joint outcome. The probability P(HÇR) is called a joint probability. 

How do you calculate a joint probability? Answer: Multiply together the probabilities on the associated tree branches. For instance,  

P(HÇR) = P(H) P(R½H) = (1/2) (2/5) = 2/10 

P(HÇB) = P(H) P(B½H) = (1/2) (3/5) = 3/10. 

Why does this make sense? What you are doing is starting with the probability of heads and then spreading it out over the subsequent possible red-blue outcomes in proportion to the red-blue probabilities: 

P(HÇR) = 2/5 of 1/2  = (2/5) (1/2) = 2/10 

P(HÇB) = 3/5 of 1/2  = (3/5) (1/2) = 3/10. 

Next we learn one more important fact: 

P(HÇR) = P(RÇH) – if and only if H is exactly the same event in both 

                                    expressions, and R is exactly the same event in both  

                                    expressions. 

In other words, suppose we reverse the process and select a wheel first, then toss the coin. If we still are working with the first of the two wheels, multiplying the probabilities on the branches of the reversed tree would give us: 

            P(R) P(H½R) = (2/5) (1/2) = 2/10. 

This is P(RÇH). We see that it gives the same result as the P(HÇR) we calculated before.   

Equipped with this last-discovered fact, we now derive a cornerstone of probability. Suppose A and B are different uncertain events where A happens and then B. We learned earlier that  

P(AÇB) = P(A) P(B½A).  

We also learned that if we keep A the same and B the same,  

P(AÇB) = P(BÇA). 

Substituting from the second expression into the first, we can write 

P(BÇA) = P(A) P(B½A). 

Solve this for P(B½A): 

P(B½A) º P(BÇA)/P(A).

 This is the famous definition of conditional probability. It is used in probability theory as a definition (thus the symbol “º”), or fundamental building block, rather than something derived from other facts.