ADVANCED LABORATORY I
FALL, 2000
GAS THERMOMETRY

Reference:  SG&N pgs. 90 - 97.

Objectives:

(1) To explore how a ideal gas thermometer can be used to measure temperature;

(2) Use measured p vs. T data to determine absolute zero when:

(a) The gas is assumed to be ideal and the vessel volume is constant with temperature;
(b) The gas is assumed to be ideal and the a temperature-dependent vessel volume is used;
(c) Non-ideality is introduced with the second virial coefficient.

(3) To critically compare the values of absolute zero, determined by modeling the results as described in 2(a) - 2(c)

Background:

    Equilibrium temperature can be defined by a physical variable that changes with temperature. This physical variable could be the height of a column of liquid mercury that increases as temperature increases, i.e. a common mercury thermometer.  Other thermometers also measure temperature by measuring the increase or decrease in volume, or other specific property of solids, liquids or gases as the temperature increases.  The physical variable whose change is fundamental to the measurement of temperature is the pressure of a fixed number of moles, n, and volume, V, of a perfect gas.  The equation of state of a perfect gas:

PV = nRT

expresses the variation of the pressure, p, with the Absolute or Kelvin temperature, T, defined by the second law of thermodynamics.  The original centigrade or Celsius temperature scale divided the temperature scale into 100 degrees from the freezing point of water at 0°C to the boiling point of water at 100°C.  The perfect gas equation of state implies that the Kelvin temperature is zero when the hypothetical perfect gas has zero pressure.  Kelvin, in defining his temperature scale kept the centigrade unit of degree, but found experimentally that the centigrade zero actually corresponded to 273.15 K and that the boiling point of water at one atmosphere pressure is 373.15 K. The two temperature scales are related by

T(Kelvin) = T(°Celsius) + 273.15.

Gas thermometry measurements must be made with real gases and the imperfect nature of these gases can be predicted using of equations of state that are adapted for real gases.  One such equation is the virial equation of state

where B, C, ... are the second, third, ... virial coefficients, is the molar volume of the gas at T and p.  The real gas in this experiment is helium whose behavior is close to ideal.  The virial expansion for He converges rapidly and only the second virial coefficient is necessary.  This experiment will use a mechanical pressure transducer to measure the pressure of a constant volume of helium immersed in various constant temperature baths defined by the co-existence of two or more phases of a substance.

Equipment and Apparatus (as pictured below):                                                               

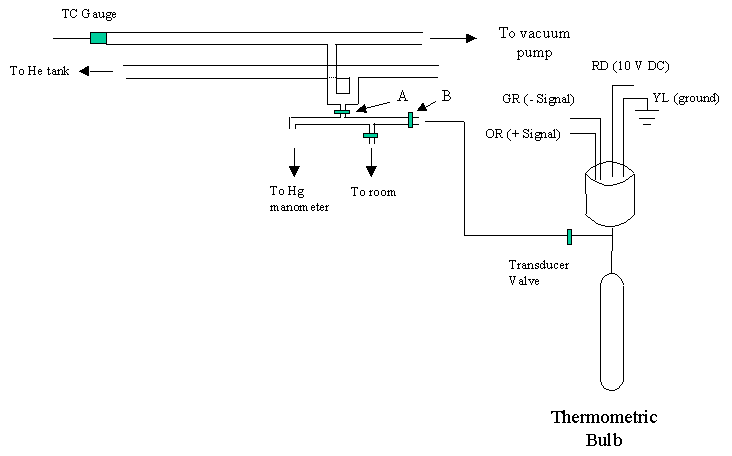
Procedures:

(1) Select one of the thermometric bulbs.  Place the bulb on the vacuum manifold and plug it in to the 6-pin ribbon cable connector (the TA will show you how to do this and assist you with use of the vacuum line).  Evacuate the entire system including both arms of the double vacuum manifold, the mercury manometer, and the thermometric bulb/pressure transducer assembly.

(2) Close valve "A" that isolates the manometer and thermometric bulb from the vacuum manifold and check that the vacuum is maintained.  Once you have ascertained this, re-open the manifold vacuum valve "A".

(3) The interfaced computer will be used to measure the pressure transducer voltage.  To begin making the readings, start the LabView computer program "Gas Thermometry" from the desktop.  Measure the voltage, V_init (corresponding to pressure) at the computer data acquisition station.  This reading will serve as the zero pressure voltage and should be subtracted from subsequent measured pressures (voltages).

(4)  Close vacuum valve "A" and flush the front arm of the vacuum manifold with helium by opening the helium valve to allow about one half an atmosphere of helium into the manifold.  The helium is evacuated and the process is repeated at least once more, leaving at most 170 mm Hg helium pressure in the manifold.  At this stage record the voltage at zero pressure. (It should still read the same as V_init.  If not, there may be a leak and you should inform your instructor.)

(5) Open the transducer valve "B" and allow sufficient time for equilibration (about 5 minutes).  You must now record the room temperature, atmospheric pressure, gauge pressure (manometer reading) and transducer voltage.  The difference in voltage (V_room minus V_init) divided by the pressure inside the bulb is the pressure calibration (volts/mm Hg) of your transducer.  Future temperature measurements will use the transducer voltage, V_T - V_init, as a measure of pressure.  Assume that the transducer voltage varies linearly with pressure.

(6) Close valves "A" and "B."  CAREFULLY, bleed up the pressure in the small manifold.  If done too rapidly, the Hg manometer will break.  Detach the thermometric bulb from the vacuum manifold.

(7) Measure the thermometric bulb temperature (pressure) at the temperature of various constant temperature baths composed of substances at phase transitions.  These should include

•  Liquid nitrogen, gaseous nitrogen

•  Solid carbon dioxide, gaseous carbon dioxide

•  Liquid water, solid water

•  Liquid water, gaseous water

(8) The pressure in atmospheres is given by the following expression:

(9) Make sure your record the bulb volume before leaving the lab.

Data Analysis: 

Note:  This is slightly different than the way your textbook treats the data.  Specifically, you will assume the temperatures of each bath and use this data to extrapolate absolute zero.

(1) Knowing the sublimation, freezing, or boiling points of the baths at standard pressure, calculate the corresponding temperatures at the actual barometric pressure of the experiment.  Do this for baths which have solid/vapor or liquid/vapor phases in equilibrium (LN2, carbon dioxide solid, and steam).  Use the Clausius-Clapyron equation, along with the temperature-independent enthalpies of vaporization or sublimation.   Reference the sources of any numbers you use.

(2) Tabulate your resultant raw data (voltages) and the resultant pressures you obtain.  Be sure that your text includes a reference to all tabulated data and equations that you use.   Assume that the dead-space volume for each of the bulbs is 3.6 mL. 

(3) Construct plots of eqs. (6) - (8) in your textbook using your data.  Analyze the data using the following successive "deviations" from ideality:

(a) Assume that He behaves like a "perfect" gas and that the vessel does not expand/contract with temperature.  Plot and fit your data according to eq. (6).

(b) Apply a volume correction to your results.  Plot and fit your data according to eq. (7).

(c) Separately apply the virial coefficient correction to your results.  Plot and fit your data accordingly.

(c) Assume that, at certain temperatures, He gas deviates from ideality AND has a temperature-dependent volume.  Plot and fit your data according to eq. (8).

           Present your data in a concise, flowing fashion.  For each model, tabulate the relevant parameters obtained from your linear regression (slopes, intercepts, errors on each).  Now, in your Discussion, compare and contrast each model by discussing goodness of fit, as determined from a inspection of your plotted residuals, the F-test and the magnitude of error associated with each absolute zero determination.  Draw conclusions about the statistical significance of using a more complex model.   Also, answer the questions given in the Discussion section of pg. 96 in your textbook.