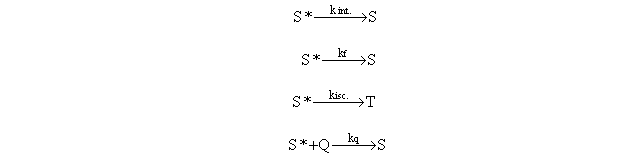Data Analysis Lab September 1

Before beginning this lab, you should have a minimum "working knowledge" of using the Excel spreadsheet program as described in your pre-lab assignment.

If you have never used Excel, you will need to spend time with the Excel tutorial and integrated help pages to learn the basics. You will also need to read S,G, & N Chapters 1, 2, 3, and 22 before beginning your assignment. While no preliminary abstract is required, a full report as described in SGN and as per instructions given in class, is expected.

Your report must include concise graphical and tabulated representations of your data and the results of your analysis. You must talk "around" ALL of your Figures, Tables, Schemes (if relevant), and Equations. Your text should be coherent, concise, and "flowing." Material that you deem to be of secondary or supplemental relevance to your arguments should be place in the Appendix.

TO DO: You are also expected to complete the Exercises in Chapter II (add these as an appendix to your final report).

Two sets of data are presented for data analysis. The first set is the vapor pressure of three substances at various temperatures. Clausius-Clapeyron theory relates the vapor pressure of a pure substance to temperature and quantities such as the heat of vaporization and the heat capacity. This theory provides an interpretation of the parameters derived by fitting to the appropriate mathematical function of the vapor pressure as it varies with temperature according to theory.

The next set of experimental data is a fluorescence decay curve obtained by the single-photon-counting method. In this case, similar to the example given in SGN, the need for appropriate weighting factors applied to the data will be demonstrated.

In both analyses, a mathematical expression is fit to the experimental data using the criterion of least squares as a measure of the goodness fit. That is, the sum of the squares of the differences of the experimental points and the mathematically predicted values is minimized with respect to a set of adjustable parameters. Theory attempts to justify the mathematical expression that is fitted to the data and allows for an interpretation of the parameters derived during the fitting process.

PART I

The Clausius Clapeyron equation may be derived by considering the Gibbs free energy of a pure substance between two phases at equilibrium. The equilibrium condition between two phases a,b is G_a(T, P) = G_b(T, P). If a temperature or pressure change perturbs the system, the condition for a new equilibrium is

The equation rearranges to the Clapyron eq.:

At equilibrium,

and, substituting in for DS from the above eq.:

For liquid to gas (vaporization) or solid to gas (sublimation) phase changes a simplification can be used. Since the molar volume of the condensed phase is much smaller than the molar volume of the gas, the molar volume of the solid (or liquid) may be ignored. Now molar volume of the gas closely approximates the volume change during the phase transition. Assuming ideal gas behavior we obtain the following relations.

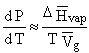
and, for an ideal gas:

using: DP/P = d(ln P). Using the above assumptions, the exact Clapyron eq. has been turned into the approximate Clausius-Clapyron equation.

If DH_vap is constant over a range of temperatures then we can directly integrate this relation to obtain equation 1.

(1)

However, if DH_vap is not constant, but instead has a temperature dependence:

Substituting this into the expression above leads to

Integration now yields equation 2.

(2)

The parameters K₁ and K₂ in the above equation allow for the inclusion of small changes in as a function of temperature. In eq. (2), K is a constant of integration.

To Do:

(1) Assume initially that does not change with temperature. Choose three substances out of the five listed below and fit, using a linear regression analysis, the vapor pressure data to obtain DH_vapaccording to equation 1. Construct a plot and the residuals as described elsewhere in this module. After reviewing a plot of the residuals (which you will put into your report) discuss whether the more detailed series in T using equation 2 (see below) is necessary to fit to the data accurately.

(2) Refit your data to the non-linear temperature-dependent DH_vap equation (eq. 2). Do this in two ways: (a) using a multiple linear least squares analysis as described in SG&N and (b) using the Solver capabilities of Excel. In both cases, construct an x-y plot, overlay your fits, and (on the same graph) display your residuals. Compare and contrast the results from each fitting process. As described in SG&N, discuss the merits of fitting to the more complex equation (fitting to eq. 1 vs. eq. 2). Consider both the statistical arguments as well as inspection of your residuals. Present in your report a tabulated summary of the thermodynamic parameters you calculated from each of the analyses. Include a detailed discussion of the criteria you used to warrant or discount the need for using the more complex equation 2. If you find that a multiple linear regression is warranted, be sure that you use the correct coefficients that correspond to each term. Your analysis should include a discussion of the correlation coefficient, simple residuals, and F-statistics that are used for determining “goodness of fit.” You should also compare and contrast the uncertainties in the parameters obtained from each analysis. You must demonstrate that you show a working “understanding” (i.e. don’t just repeat the definitions given in the book, but discuss, in your own words) of what each of these statistical quantities mean. Be sure to watch your significant figures on your results and errors of all of tabulated data.

TABLE I: Vapor Pressure Data
Vapor pressures (mm Hg) of less than one atmosphere as a function of temperature. (All temperatures are in degrees Celsius)

Chemical	1	5	10	20	40	60	100	200	400	760 mm Hg
Sodium	439	511	549	589	633	662	701	758	823	892 ^oC
1,4-Dioxane	-35.8	-12.8	-1.2	12.0	25.2	33.8	45.1	62.3	81.8	101.1^oC
Acetone	-59.4	-40.5	-31.1	-20.8	-9.4	-2.0	7.7	22.7	39.5	56.5 ^oC
Butyric Acid	25.5	49.8	61.5	74.0	88.0	96.5	108.0	125.5	144.5	163.5 ^oC
Stannic Chloride	-22.7	-1.0	10.0	22.0	35.2	43.5	54.7	72.0	92.1	113.0 ^oC

For this section you will need to obtain a copy of the file “DAData.xls,” available from the above link. This file is a simulated copy of fluorescence decay data obtained by the single photon counting method. In this experiment the fluorescence intensity is used as a direct measure of the concentration of the emitting species (S*). In this case S* decays according to the following set of parallel reactions.

From your vast experience in kinetic analysis you know that this data conforms to equation 3 (you must derive this equation in the theory section of your report):

where [S*]_t is the time-dependent concentration of emitting species, A is a pre-exponential factor that depends on the quantum yield of fluorescence and other experiment conditions (i.e. light intensity, sample geometry, etc.), k is the sum of all first order and pseudo-first order decay constants and t is the time in seconds.

Fit the data in "testdata" to equation 3 and obtain a residuals plot. Do this in three ways:

(a) Linearize the equation by taking the log of both sides. Plot the data points, fit, and residuals. Remember to transform the residuals back to [S*] units (do not use ln [S*]).

(b) After review of the example on page 716-718 in SGN refit the data with appropriate weighting factors and obtain a new residuals plot recognizing that fluorescence data does follow a Poisson distribution. Compare this plot with the one obtained previously. If possible compare the values obtained for the fitting parameters A and k in the two cases used. What do you think is the best guess at the true values of these parameters and why. You will than apply the weighting factor to the residuals and replot the weighted residuals (while this is not strictly correct it is the best you can do with Excel).

In cases (a) - (c), your report should include a plot of [S*] vs time with overlaid fits of the data. Residual plots (on the same graph) should be included. When weighting your data, the weighted residuals should also be included. Include in your discussion the statistical analyses described above in Part I. Compare, contrast, and critically discuss the results obtained from each analysis. Be sure to watch your significant figures on your results and errors of all of tabulated data.