Introduction to Treaps
A treap is a combination of a binary search tree (BST) and a heap. You should be very familiar with BSTs at this point in the semester, but you probably haven't encountered heaps yet. For this project, you only need two concepts from heaps:
- Each node of the tree, in addition to holding a data value, will also store an integer priority value. Priority values should be unique; that is, no two nodes should have the same priority.
- The tree must have the Max-Heap Property: for any node \(w\) in the tree, the priority of \(w\) must be greater than the priorities of its two children.
The following figure shows a treap in which the data are letters (or strings) and the priorities are integers.
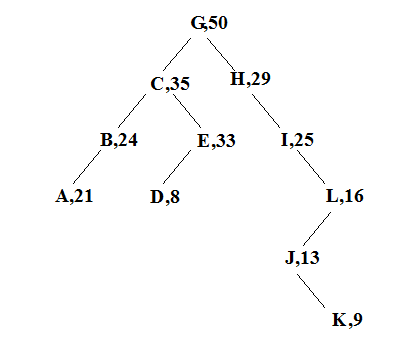
(Image source: http://cseweb.ucsd.edu/~kube/cls/100/Lectures/lec5/lec5-2.html#pgfId-955731)
A treap must be both a BST and have the max-heap property, which means insertions and deletions must check that the max-heap property holds and fix the tree if it does not. It will turn out that this is not as bad as it sounds. The max-heap property can always be repaired by applying single rotations.
Tree Rotations
Single tree rotations are local modification to a tree that can be used to repair violations of the max-heap property while maintaining the BST structure. The restructurings that can be achieved using single rotations are a subset of those possible with trinode restructuring. The figure below illustrates left and right single rotations.
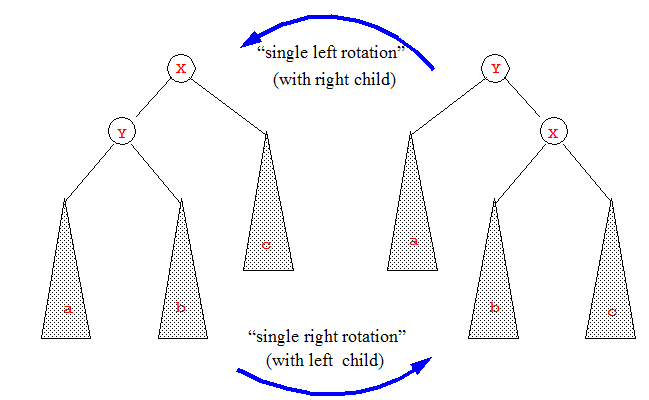
(Image source: http://cseweb.ucsd.edu/~kube/cls/100/Lectures/lec5/lec5-5.html#pgfId-955859)
It is not difficult to see that rotations preserve the BST ordering: in both images, we have \(a < Y < b < X < c\), and we assume that the subtrees \(a\), \(b\), and \(c\) were constructed correctly before the rotation occured. How dow we use rotations to make local fixes to the max-heap property? Suppose that in the left picture, the priority of \(Y\) were higher than the priority of \(X\), violating the max-heap property; then a right rotation would make \(Y\) the parent of \(X\), correcting the error.
We can use single rotations, along with standard BST operations, to maintain a treap.
-
Insertion: suppose we have a value-priority pair \((v, p)\) that we wish to insert into a treap. Assume that \(p\) is unique. We first perform a normal BST insertion, which creates a new leaf node. Then, if \(p\) is greater than the priority of the parent, we do a left or right single roation to move \((v, p)\) up in the tree.
Now \((v,p)\) will have a new parent, and it is possible that \(p\) is still larger than the new parent's priority, in which case we perform another rotation; repeat, moving \((v,p)\) up the tree, until the max-heap property is satisfied at each node.
-
Deletion: suppose we wish to remove the node with value \(v\). We begin with a normal BST search to see if \(v\) is in fact in the tree; if not, do nothing.
If we find \(v\) and it is a leaf node, we can simply delete the node. If it is not a leaf node, perform a sequence of left and right rotations to move \(v\) down the tree until it is a leaf, and then delete it. When performing the rotations, you should choose the direction (left or right) that moves the child with largest priority higher in the tree.
So why bother with treaps? One interesting fact is that if we build a treap using random priorities it will almost always be balanced (meaning, balanced with high probability); at the same time, treaps are easier to implement than balanced trees such as AVL or red-black trees. Also, there are other operations that can be performed efficiently on treaps, such as joining two treaps to create a single combined treap, or splitting a treap into two treaps.
Example
Insert \((F, 40)\) into the following treap:

Example
Delete the node containing “C” in the following treap:

A good reference for additional information is this lecture on treaps from UCSD.