Project 3: Splay Tree of Trees
Due: Tuesday, April 7, before 9:00 pm
Addenda
- Extension: The final due date for Project 3 has been extended to Monday, April 13, before 9:00 pm.
-
Function Clarifications:
- BST::insert() should return true if a new element is inserted; it should return false if the insert fails, e.g. if there is already an element of the given rank.
- Scanner::insert() should return false if the insert fails for any reason. For example, if the weight is out-of-bounds or the BST insertion fails.
- Files can only be loaded one time into a Scanner object. The Scanner::loadFiles() function should check whether files have already been successfully loaded and, if so, return false.
-
Point Distribution:
- 70 points — BST class and test program.
- 30 points — Scanner class and test program.
- Late Penalties: project late penalties will be waived for the remainder of the semester. However, no project will be accepted after the three-day-late deadline (Friday after the due date, before 9:00 pm).
Objectives
The objectives of this programming assignment are:
- Practice constructing and using binary search trees.
- Practice writing basic rebalancing routines.
- Practice implementing a self-balancing tree.
- Gain experience with function pointes and file input.
Introduction
BST with Array-based Rebalancing
In computer science, however, laziness is sometimes a viable strategy. Why do today what you can put off until tomorrow? Especially if there is a chance that you won't actually have to do it tomorrow, either?
In contrast to AVL trees and Red-Black Trees in which we use fiddly rotations and restructurings to maintain \(O(\log n)\) height, with array-based rebalancing, when an imbalance occurs we copy the entire imbalanced subtree to an array and rebuild it as balanced as possible. On the plus side, this is easier to implement than other restructurings, but it is certainly much slower. Therefore, we may want to rebalance less frequently, waiting until the tree is really out-of-whack. Insertion proceeds in the same manner as in an unbalanced binary search tree, until we detect an imbalance, at which point we fix the imbalance using the array-based method.
When a subtree is rebalanced, we convert the entire subtree into a sorted array. Then we convert the array back into a perfectly balanced BST. Rebuilding is easy because the array is sorted. We can find the middle element of the array in constant time and make it the root of the new subtree. Then, we recursively build the left subtree and the right subtree using, respectively, the portion of the array that has keys smaller than the root and the portion of the array that has keys larger than the root. The result is a binary search tree that is as balanced as possible. (See Project 3 Examples.) The rebalance procedure takes \(O(t)\) on a BST subtree with \(t\) elements.
For this BST implementation, the user determines the balance criteria for the tree by implementing a balance function that returns true if a node is imbalanced and returns false otherwise. The function is passed to the BST class using a function pointer. The function must take four integer arguments, in this order: leftHeight, rightHeight, leftSize, and rightSize. However, the function doesn't have to use all four arguments. For example, here is a function that implements the AVL height-balanced property:
bool imbalfn(int leftHeight, int rightHeight, int leftSize, int rightSize) {
return (leftHeight > rightHeight + 1) || (rightHeight > leftHeight + 1);
}
As was mentioned previously, array-based rebalancing is expensive; using the AVL height-balanced property may not be very efficient as it tends to rebalanced frequently. Fortunately, it's easy to try other criteria by using a different balanced function with the constructor.
One note about the rebalance procedure: it is possible to have two nodes \(x\) and \(y\) needing rebalancing \(x\) is an ancestor of \(y\). In this situation, we want to do the rebalancing at \(x\) since rebalancing the subtree rooted at \(x\) will also rebalance the subtree rooted at \(y\). If we rebalanced at \(y\) first, the time spent rebalancing at \(y\) is completely wasted since all that work is undone when we rebalance at \(x\). (See Project 3 Examples.)
Splay Trees
Another type of “balancing” is used in a type of binary search tree called Splay tree. Basically, a splay tree is a type of binary search tree that throws the idea of normal balancing out the window, and focuses on the problem of accessing the same item over and over again. This results in a worst case running time for insertion and search of \(O(n)\), but this is a tradeoff for the ability to access the last item used in \(O(1)\) time. This structure achieves this through the use of one principle: whenever an item inserted or accessed through a search, it will become the new root of the tree.
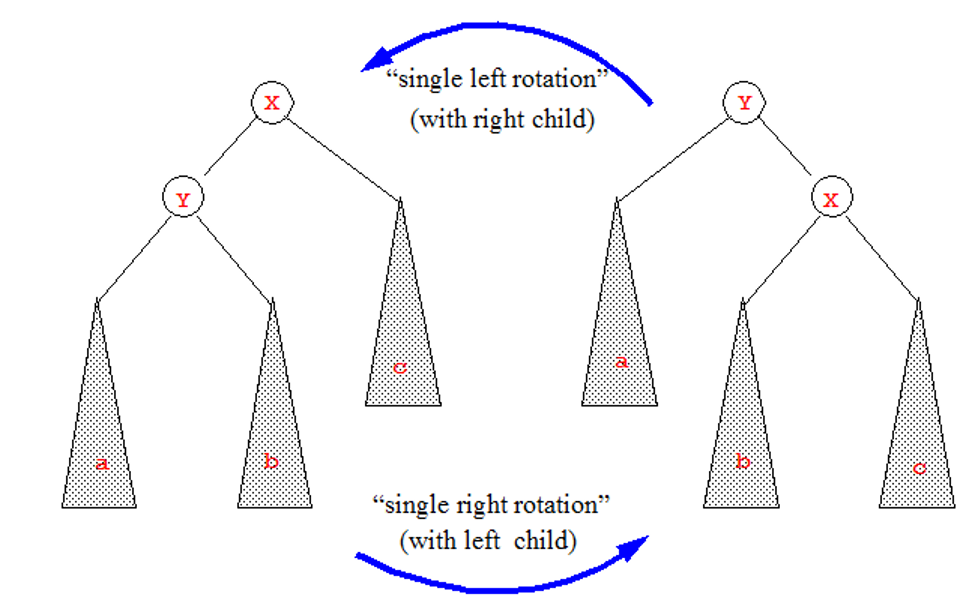
For this project, we will only focus on the insertion and search functions of a splay tree. Before fully understanding how a splay tree searches, we need to emphasize a couple of sub-tasks a splay tree should be able to achieve. The first one is rotations. The figure below illustrates left and right rotations:
(Image source: http://seweb.ucsd.edu/~kube/cls/100/Lectures/lec5/lec5-5.html#pgfId-955859
It is not difficult to see that the ordering of the tree is preserved after rotating. In both images, we keep the \(a < Y < b < X < c\) relationship, and we assume that the \(a\), \(b\), and \(c\) trees were constructed correctly before the rotation occurred. For now, we will refer to these rotations as Zig (right rotation) and Zag (left rotation). These operations will help us better understand the four different cases in which we rotate in order to bring the node we searched for to the root.
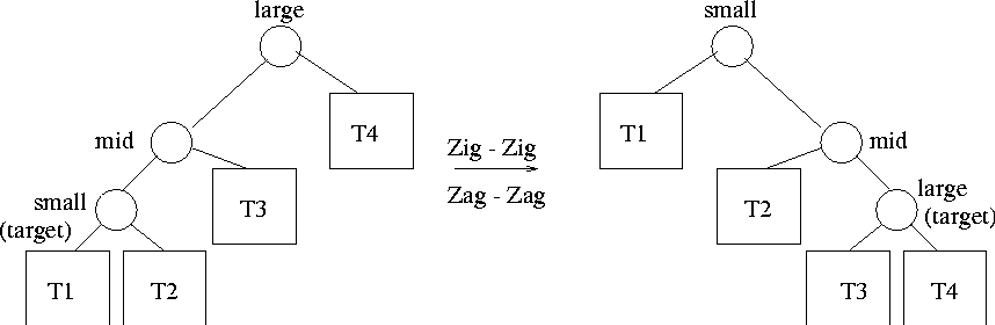
- Zig-Zig: Node is the left child of its parent, and the parent is also the left child of the grand parent.
- Zag-Zag: Same as last case, except the nodes are positioned in the right subtrees.
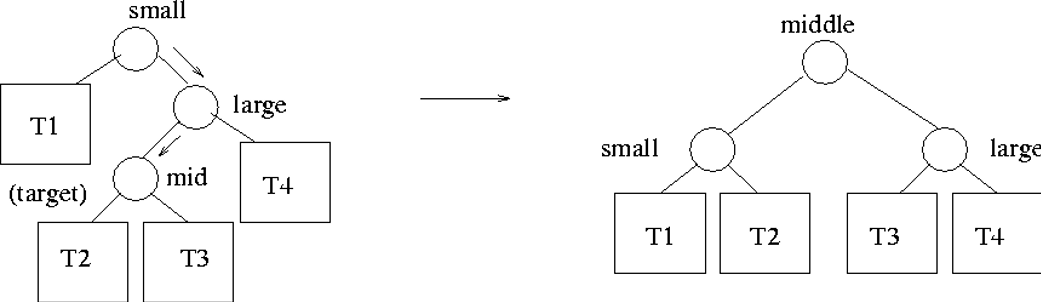
- Zig-Zag: Node is the left child of its parent, and the parent is the right child of the grandparent.
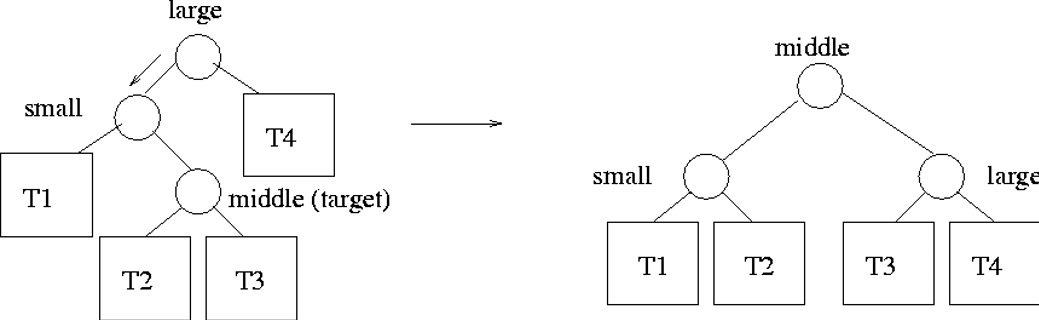
- Zag-Zig: Node is the right child of its parent, and the parent is the left child of the grandparent.
Finally, the following diagram shows how we are able to pull a node we searched for to the root. Suppose we searched for node \(C\); we move it to the root by applying the operations described above:
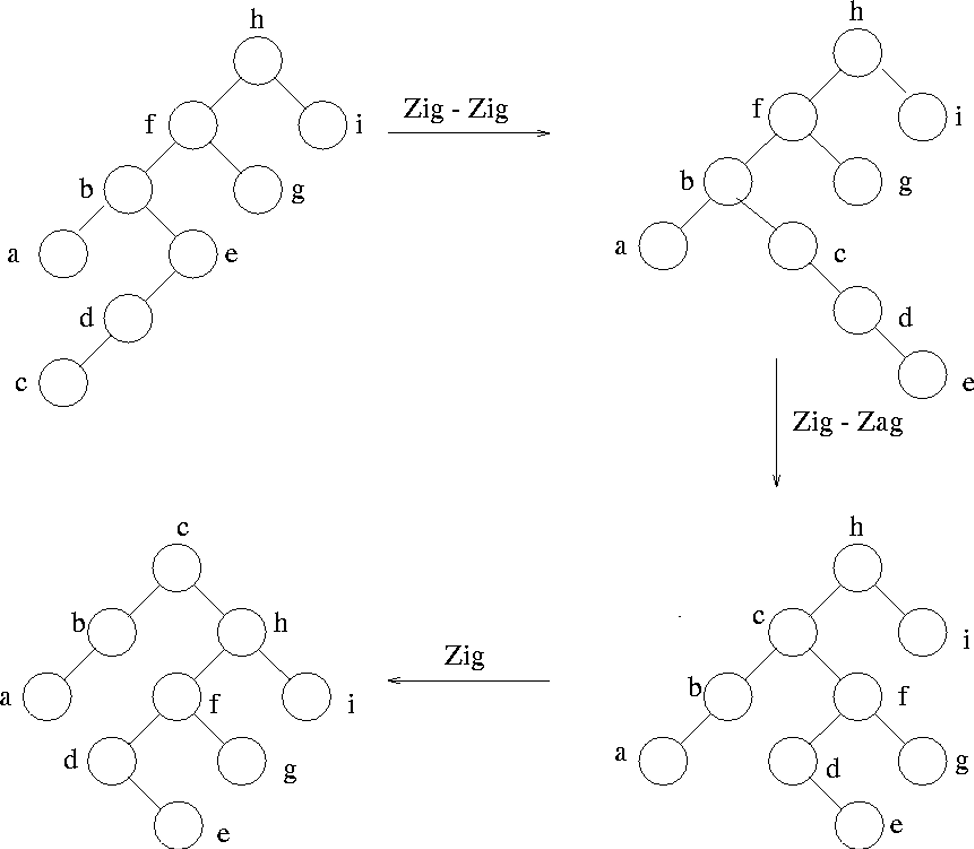
(Image source: http://lcm.csa.iisc.ernet.in/dsa/node93.html)
Tree of Trees!
Suppose that some hacker with malicious intent has taken over your collection of ascii art images. For each image, he scrambled it and gave each ascii character a number. On top of that, he left a strange file called weights.txt, which you believe has to do with your now scrambled image. You deduce that these weights are also scrambled and they correspond to each character in your original image. With this knowledge, you devise a plan to recover your images.
For example, assume the following ascii art is composed of the letters a,b, and c:
A B B C (this is how the original ascii art should look like)
Then, you are given two files, one with your scrambled ascii art and one with the weights. The files may look like this:
2 3 1 2 (this is your scrambled ascii art)
2 4 1 3 (this is what the weights file looks like)
If you assign the ascii characters to the numbers in your scrambled file we have that A = 1, B = 2, C = 3. So then, our two files would look like this:
Scrambled file before char assignment 2 3 1 2
Scrambled file after char assignment B C A B
Weights.txt 2 4 1 3
Now, you know that the dimensions of your original file were 2x2, so you know that weights.txt is just a file containing the numbers 1 through 4 and you can use these numbers to reverse the scrambling! For example:
Original image A B B C
What weights.txt should look like after fix 1 2 3 4
The weights just map the positions of characters in the file. Now, it’s up to you to devise a way to reverse the scrambling! (not really, the right implementation is given below).
Since you just learned about binary search trees and splay trees, you think it’s a good idea to use them for solving each image. The plan is as follows:
- You plan to have several binary search trees, one for each line of your image into which will insert the correct characters for that row.
- These binary search trees will sort the characters by their weights given in weights.txt.
- To make things a little more interesting, rather than storing the binary trees in a vector, we will store them in a splay tree: each node in the splay tree will include a pointer to a BST. The splay trees will be ordered by their weight range.
- After they are sorted, you just have to print out each tree in the same line order, and you will have your restored image!
For instance, if you were fixing the image from the previous example, you would have two trees (since there are only two lines). You will insert the characters along with the weights into the right tree so that tree one contains the weights 1 and 2, and tree two contains the weights 3 and 4. If you print out tree one and then tree two, you will obtain the original image.
Assignment
Your assignment is to implement this algorithm by completing a BST that supports array-based balancing; the BST class will be used to store each line of the ascii art file. Since there might be a lot of trees created, we will be using a splay tree to organize the BSTs. This will be efficient if we end up inserting several weights that belong in the same BST: the splaying operation moves the most recently accessed node to the root, allowing \(O(1)\) access when accessing the same BST repeatedly. In short, this assignment is an implementation of a splay tree of binary search trees, where each node in the splay tree will contain the root of a binary search tree.
For this project, you are provided with the following files:
Note: driverOutput.txt doesn't display correctly in a web browser; download it, e.g. to GL, and cat the file to see the ASCII art image.
These and all the provided project files are available on GL:
You may not change any of the private variables or public function declarations. Also, any provided function implementations may not be modified. You may, however, add your own private variables and functions and additional “using” statements.
You are responsible for thoroughly testing your code. You must implement and submit two test files:
- bstTest.cpp — it is important that you develop and test the BST class first since Scanner won't work without a working BST.
- scanTest.cpp — tests the functionality of your Scanner class.
As always, make sure you get rid of those memory leaks and errors!
Specifications
BST Class
-
Constructor. Must pass a pointer to a balance function; the function pointer type balfn_t is defined in BST.h. The function pointer must be saved in the _imbalanced class variable.
BST(balfn_t imbalanced);
-
Copy constructor. Must make a deep copy and should function properly on an empty tree.
BST(const BST& rhs);
-
Assignment operator. Must make a deep copy, function properly with an empty right-hand side, and protect against self-assignment.
BST& operator=(const BST& rhs);
-
Destructor. Must free all memory used by the tree.
~BST();
-
Insert a (key, data) pair into the tree. Begin with a standard BST insertion; check for imbalances after insertion and rebalance as necessary.
bool insert(string data, int key);
-
Get the size of the tree (number of nodes). This function is already implemented in BST.cpp.
int size() const;
-
Get the height of the tree. This function is already implemented in BST.cpp.
int height() const;
-
Print the data in the tree using an inorder traversal; if verbose is true, print the tree structure including sizes, heights, and parentheses. If verbose is false, just print the data.
void dump(bool verbose = false) const;
Scanner Class
-
Scanner constructor. Pass in the number of lines in the image (lines), the number of characers per line (range), and a vector of strings containing the ASCII characters corresponding to the indices in the scrambled image; e.g., chars[0] is the character corresponding to “1” in the ASCII file, chars[1] corresponds to “2”, etc.
Scanner(int lines, int range, vector
chars); -
Scanner destructor. Must delete the splay tree and all of the BSTs.
~Scanner();
-
Copy constructor. Must make a deep copy and should function correctly when the right-hand side is empty.
Scanner(const Scanner& rhs);
-
Assignment operator. Must make a deep copy, function correctly when the right-hand side is empty, and protect against self-assignment.
Scanner& operator=(const Scanner& rhs);
-
Insert (character, weight) pair; splay the node in which the pair is inserted. Return false if insertion fails, e.g. if the weight is out-of-bounds; return true otherwise.
bool insert(int weight, int ch);
-
Load the data files (ASCII file and weights file) and insert data into the data structure. Returns false if either file fails to open; returns true otherwise.
bool loadFiles( string ascii, string weights );
-
Prints the unscrambled ASCII art. Does an inorder traversal of the splay tree, calling the BST dump() method for each BST.
void dump() const;
-
Prints an inorder traversal of the splay tree, printing the bounds (upper:lower) for each node in the splay tree. Prints parentheses to show the structure of the tree.
void inorder() const;
Additional Requirements
Requirement: Your BST class must implement array-based rebalancing and must support the use of user-supplied balance functions as described in the Introduction. Your implementation will be tested with various balance functions, some based on heights, others on size.
Requirement: When called with verbose = true, the BST inorder() function must print an inorder traversal of the BST. For each node in the tree, it must print _data, _height, and _size, separated by colons. It must also print parentheses to show the structure of the tree (see the sample output in bstOutput.txt).
Requirement: the Scanner class must implement a splay tree in which each node contains a pointer to a BST. Each SNode in the splay tree stores the range of weights that are stored in its BST; these determine the ordering of the SNodes. After every insertion, the inserted SNode must be splayed.
Requirement: The inorder() function of the Scanner class must print an inorder traversal of the splay tree. For each node, it must print the upper and lower weight bounds, separated by a colon. Parentheses must be printed to show the tree structure (See the sample output in driverOutput.txt).
Requirement: You may not use any additional STL containers, and vector may only be used to store the string vector _chars.
Implementation Notes
- Start by implementing a basic BST without balancing. When that is working, then add the balancing. Thoroughly test the balanced BST before attempting to implement the Scanner class.
- There are two times that you can check if a BST node is imbalanced: as you are recursing down the tree to perform an insertion, or as you are returning from recursive calls, moving back up the tree. It is more efficient to check when moving down the tree to avoid restructuring at a node \(x\) only to restructure again at an ancestor node \(y\); however, this may leave the tree slightly imblanced.
What to Submit
You must submit the following files to the proj3 directory.
- BST.h
- BST.cpp
- Scanner.h
- Scanner.cpp
- bstTest.cpp
- scanTest.cpp
If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.