Project 1: Adjacency Lists

Due: Tuesday, February 18, before 9:00 pm

Addenda

Added a section on testing your project. These are tests you should consider including in your mytest.cpp program.
Added an implementation note about returning entries in reference parameters to EntryList::remove() and EntryList::getEntry().

Objectives

Develop C++ programming abilities using object-oriented design, dynamic memory allocation, array manipulation, iterators, and exceptions.
Understand graphs and the adjacency list representation of a graph; implement the adjacency list representation.
Understand the concepts and implemtation of dyanically-resized arrays.

Introduction

In computer science and discrete mathematics, a graph is not a plot of y = f(x). A graph has vertices and edges. Here's a simple example:

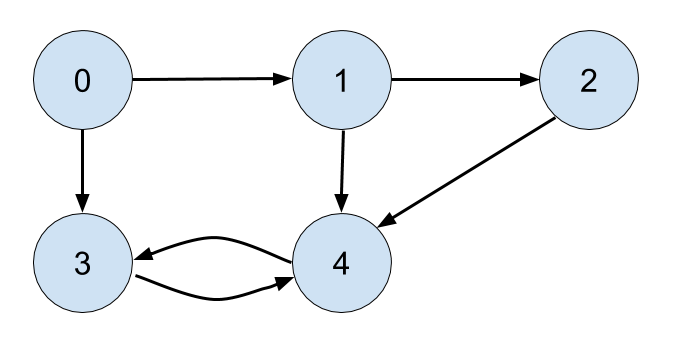
The vertices are the circles, and the edges are the lines between the vertices. It is common to use the words “node” and “vertex” interchangeably.

In the example above, the set of vertices is \(\{0,1,2,3,4\}\) and the set of edges is \(\{(0,1), (0,3), (1,2), (1,4), (2, 4), (3,4), (4,3)\}\). It is common to use the ordered pair notation \((u, v)\) to represent an edge. This graph is an example of a directed graph: each edge has a direction. The edge \((u, v)\) goes from vertex \(u\) to vertex \(v\).

Note that it is possible to have edges in both directions, such as \((3,4)\) and \((4,3)\) in the example. Also, a vertex is allowed to have an edge to itself, called a self-edge. There are certain applications in which it is useful to have self-edges.

A weighted graph has numeric weights associated with the edges. This may seem like a strange thing to do, but it is natural in many applications. For example, suppose your graph represents nodes in a network and edges represent network connections; then the edge weights could indicate the bandwidth of the connection. In the figure below, we've added some arbitrary edge weights to our original example.

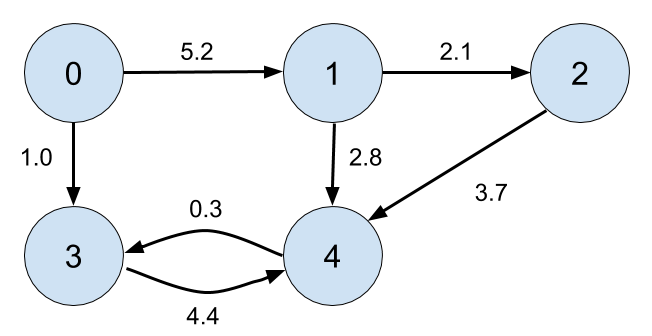
A weighted edge from \(u\) to \(v\) with weight \(w\) is represented by a tuple \((u,v,w)\). The weighted edges of the example graph are \(\{(0,1,5.2), (0,3,1.0), (1,2,2.1), (1,4,2.8), (2, 4, 3.7), (3,4,4.4), (4,3,0.3)\}\).

One common way to store a graph is using an adjacency list data structure. Typically, this is an array of linked lists, one list for each vertex; however, for this project, we will use dynamically-resized arrays rather than linked lists. The following figure represents the adjacency list data structure for the sample weighted graph.

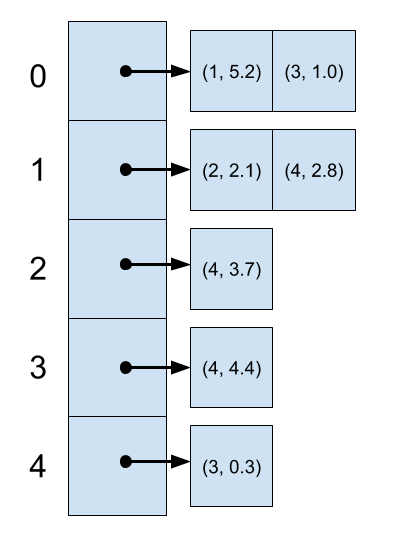
Here the first dynamic array, indexed by 0, has the neighbors of vertex 0. The neighbors of a vertex \(u\) are the vertices \(v\) such that \((u, v)\) is an edge in the graph. The dynamic array for vertex \(u\) will contain all neighbors \(v\) of \(u\) along with the edge weights. For example, the dynamic array for vertex 1 in our sample weighted graph contains the pairs \((2,2.1)\) and \((4,2.8)\).

Dynamic Arrays

A limitation of C/C++ arrays is their fixed size: once an array of \(n\) elements is created, it is forever limited to storing at most \(n\) elements. Thus we frequently create arrays that are larger than we expect to need, which is an inefficient use of memory. Dynamic arrays are able to resize themselves as necessary, expanding if we attempt to insert into an array that is full, and contracting when only a small portion of the array is being used. The STL vector container is an implementation of dynamic arrays.

The size of a dynamic array is the number of elements currently in the array and the capacity is the amount of allocated space. There are efficient strategies for expanding and contracting a dynamic array:

Expansion. If the user attempts to insert an entry into a dynamic array that is already full, the capacity should be doubled.
1. Create a temporary array with twice the capacity.
2. Copy the elements from the original array to the temporary array.
3. Delete the original array.
4. Assign the temporary array to the original array.
Contraction. After removing an entry, if the size is less than one-fourth of the capacity, cut the capacity in half.
1. Create a temporary array with half the capacity.
2. Copy the elements from the original array to the temporary array.
3. Delete the original array.
4. Assign the temporary array to the original array.

See Section 6.1 of the textbook for more information about dynamic arrays (called extendable arrays in the textbook).

Assignment

Your assignment is to implement the sparse adjacency list data structure Graph that is defined in the header file Graph.h. The dynamic arrays that store the neighbor lists are implemented in a second class, EntryList, which is defined in EntryList.h. Thus, to complete the Graph class, you must first implement the EntryList class.

Additionally, you must write a test program that fully exercises your implementations of both classes. The test program must be named mytest.cpp.

Provided Files

EntryList.h: definition of the EntryList class.
Entrylist.cpp: a skeleton implementation file for EntryList.
Graph.h: definition of the Graph class.
Graph.cpp: skeleton implementation of Graph.
driver1.cpp: a sample driver for the Graph class.
driver1.txt: sample output from driver1.cpp.
driver2.cpp: a sample driver for the Graph class.
driver2.txt: sample output from driver2.cpp.

All of these files are also available on GL in the directory:

/afs/umbc.edu/users/c/m/cmarron/pub/www/cs341.s20/projects/proj1files/

About Iterators

Both the EntryList and Graph classes include iterators. The purpose of an iterator is to provide programmers a uniform way to iterate through all items of a data structure using a for loop. For example, using the Graph class, we can iterate thru the neighbors of vertex 4 using:

Graph::NbIterator nit ; for (nit = G.nbBegin(4); nit != G.nbEnd(4) ; nit++) { cout << *nit << " " ; } cout << endl ;

The idea is that nit starts at the beginning of the data for vertex 4 and is advanced to the next neighbor by the ++ operator. The for loop continues as long as we have not reached the end of the data for vertex 4. We check this by comparing against a special iterator for the end, nbEnd(4). This requires the NbIterator class to implement the ++, != and * (dereference) operators.

Similarly, the Graph class allows us to iterate through all edges of a graph using a for loop like:

Graph::EgIterator eit ; tuple<int,int,weight_t> edge ; for (eit = G.egBegin() ; eit != G.egEnd() ; eit++) { edge = *eit ; // get current edge cout << "(" << get<0>(edge) << ", " << get<1>(edge) << ", " << get<2>(edge) << ") " ; } cout << endl ;

Since a program may use many data structures and each data structure might provide one or more iterators, it is common to make the iterator class for a data structure an inner class. Thus, in the code fragments above, nit and eit are declared as Graph::NbIterator and Graph::EgIterator objects, not just NbIterator and EgIterator objects.

The `EntryList` Class

An EntryList object is a dynamically-resized array of Entry objects; an Entry stores a vertex and weight (the Entry class is fully implemented in EntryList.h). The EntryList class is required to store Entry objects in order of increasing vertex number, and vertex numbers must be unique.

In addition to providing basic creation, retrieval, update, and deletion operations, the EntryList class provides an iterator which can be used to iterate through the elements of the list. For example, the following code would print all the entries in an EntryList named EL:

EntryList::Iterator itr ; for ( itr = EL.begin(); itr != EL.end() ; itr++ ) { cout << *itr << " " ; } cout << endl ;

You must complete the implementations of the following functions of the EntryList class:

Default constructor. Creates an EntryList with capacity DEFAULT_SIZE.
Copy constructor, assignment operator, and destructor.
Insert the entry e. The elements of the list must be kept in increasing order by vertex. If inserting the new element would exceed the capacity of the EntryList, then the array must be expanded, doubling the capacity. Returns true if new entry inserted, false if there is already an entry with the same vertex as e.
Update the entry e; return true if an entry with the same vertex as e exists and was updated, false if there is no entry with the same vertex as e.
Get the entry with given vertex value; return the entry in ret. Returns true if an entry with the specified vertex was found, false if there is no entry with the specified vertex.
Remove the entry with given vertex value; return the entry that was removed in ret. If, after successfully removing an Entry, the number of entries is less than 1/4 of the capacity, then the EntryList array must be contracted, halving its capacity. The capacity must never be reduced below DEFAULT_SIZE, a constant defined in EntryList.h. Returns true if an entry with the same vertex as e exists and was removed, returns false if there is no entry with the specified vertex.
Access an element of the EntryList by index. Throws range_error if indx is not a valid index into the EntryList array.

WARNING: at() allows modification of an entry, but changing the vertex value could ruin the ordering of the entries!
Get the size of the EntryList (numer of Entries actually stored). This function is already implemented and must not be modified.
Get the capacity (size of _array; number of entries that could be stored without resizing). This function is already implemented and must not be modified.
Dump the contents of _array. For debugging.
Create a “begin” iterator for an EntryList object.
Create an “end” iterator for an EntryList object.

The `EntryList` Iterator Class

Additionally, you must implement the EntryList::Iterator class. The iterator is implemented as a inner class of EntryList.

Constructor for iterator for an EntryList object; indx can be used to set _indx for begin and end iterators.
Comparison operators for EntryList iterators.
Advance the iterator to the next entry; if the iterator is already at the end, leave it unchanged.
Return the entry at the current iterator position.

The `Graph` Class

The Graph class implements the adjacency list representation of a graph. It uses EntryList objects to store neighbor lists.

The Graph class has two iterator classes: a neighbor iterator (NbIterator) and an edge iterator (EgIterator). Given a vertex v in the graph, the neighbor iterator can be used to iterate over all neighbors of v; it is really just a wrapper on the EntryList::Iterator class. The edge iterator can be used to iterate over all the edges in the graph. The edge iterator implementation is a bit more involved, but still should make use of the iterator for EntryList.

The following functions must be implemented to complete the Graph class:

The Graph constructor; the number of vertices (n) must be provided. Throws invalid_argument if n \(\leq 0\).
Graph copy constructor, assignment operator, and destructor.
Returns the number of vertices.
Returns the number of edges.
Add an edge between u and v with weight x. Throws invalid_argument if u or v is not a valid vertex number.
Remove the edge (u, v). Returns true if an edge is removed; false if there is no edge (u,v). Throws invalid_argument if u or v is not a valid vertex number.
Prints the Graph data structure. For debugging.
Create a “begin” edge iterator for a Graph object.
Create an “end” edge iterator for a Graph object.
Create a “begin” neighbor iterator for the neighbors of vertex v in a Graph object.
Create an “end” neighbor iterator for the neighbors of vertex v in a Graph object.

The `Graph` Iterator Classes

Additionally, you must implement the Graph::EgIterator and Graph::NbIterator classes. The iterators are inner classes of Graph.

`Graph::EgIterator`

EgIterator(Graph *Gptr = nullptr, bool enditr = false);
The edge iterator constructor.
- If Gptr is nullptr, create an unitialized iterator.
- If Gptr points to a host Graph object:
  1. If enditr == false, create a begin iterator.
  2. If enditr == true, create an end iterator.
Compare two edge iterators. Mainly used to test if the iterator has reached the end iterator in a for loop.
Advanced the iterator to the next edge; if already at the end() iterator, leave unchanged. Throws invalid_argument if the iterator is uninitialized.
Return the edge at the iterator position as a tuple (u, v, weight). Throws invalid_argument if the iterator is uninitialized or if derefrence of _itr failes.

`Graph::NbIterator`

NbIterator(Graph *Gptr = nullptr, int v = 0, bool enditr = false);
Constructor for a neighbor iterator.
- If Gptr is nullptr, create an unitialized iterator.
- If Gptr points to a host Graph object:
  1. If enditr == false, create a begin iterator for vertex v.
  2. If enditr == true, create an end iterator for vertex v.
Throws invalid_argument if Gptr is not nullptr and v is not a valid vertex for the graph pointed to by Gptr.
Compare two neighbor iterators. Mainly used to test if the iterator has reached the end iterator in a for loop.
Advance the iterator to the next neighbor. If it is already at the end() position, leave the iterator unchanged.
Returns the neighbor and weight at the current iterator position as a pair. Throws invalid_argument if the iterator is uninitialized or invalid.

Additional Requirements

Be sure to read the function descriptions carefully — your implementation is expected to behave as described in this document. Following are additional project requirements.

Requirement: You may not use any Standard Template Library (STL) classes other than pair and tuple in the implementation of EntryList and Graph. You may use STL classes in mytest.cpp.

Requirement: your code must compile with the original Graph.h header file. You are not allowed to make any changes to this file.

Requirement: You may add private helper functions to the EntryList class, but they must be declared in EntryList.h. No other modifications to EntryList.h are permitted.

Requirement: per the course coding standards, your code must compile with g++ on the GL servers without using any compilation flags.

Requirement: a program fragment with a for loop that uses your NbIterator must have worst case running time that is proportional to the number of neighbors of the given vertex.

Requirement: a program fragment with a for loop that uses your EgIterator must have worst case running time that is proportional to the number of vertices in the graph plus the number of edges in the graph.

Implementation Notes

Implement and test the EntryList class before attempting to implement Graph. Be sure to test all the functions of the class and the iterator
The iterator classes do not need destructors, copy constructors, or overloaded assignment operators because they do not have any dynamically allocated data members. The compiler supplied destructor, copy constructor, and assignment operator will do the right thing.
Graphs are allowed to have vertices that do not have any edges. The EgIterator constructor should work correctly even if vertex 0, 1, 2 ... have no edges. Similarly, the ++ operator for the EgIterator should be able to handle vertices with no edges.
The functions EntryList::getEntry() and EntryList::remove() both return an Entry object through a reference parameter. Within the implementation of the functions, ret must be set equal to the Entry to be returned.

Testing

Following is a non-exhaustive list of tests to perform on your implementation.

`EntryList`

Basic tests of insert(), update(), remove(), and getEntry:

Create an EntryList; insert a number of entries; check that contents of the list are correct.
Update some of the entries; check that the contents of the list are correct.
getEntry() returns the desired entry in the ret reference variable. Similarly, remove() returns the entry that was removed in ret.
Remove some of the entries; check that the contents are correct.
Check that entries are ordered by increasing vertex after some combination of insertions and removals.
Check that there are no duplicate vertex values in the entries after some combination of insertions and removals.

Tests of the copy constructor and assignment operator:

Copy and assignment create a copy with the correct data.
Copy and assignment create a deep copy.
Copy and assignment function correctly when the source object is empty.
Assignment protects against self-assignment.

Miscellaneous tests:

All functions that return a bool status return the correct value.
at(int indx) throws range_error if indx is not a valid index.
Expansion functions correctly. For example, insert 10 entries; check capacity; insert another entry; capacity should double.
Contraction functions correctly. For example, insert 11 entries; check capacity; remove seven entries (so size falls to four); check capacity.
Iterator-based for loop lists entries in array order and terminates correctly.
Iterator-based for loop functions correctly for an empty EntryList.
*begin() returns first element of non-empty EntryList; begin() != end() unless the EntryList is empty.
Test for memory leaks and errors using Valgrind.

`Graph`

Basic tests of constructor, addEdge(), and removeEdge():

Constructor throws invalid_argument if \(n \leq 0\).
Perform combinations of insertions and deletions, checking that the contents of the data structure are correct.
addEdge() and removeEdge() throw invalid_argument if passed an invalid vertex number.

Tests of the copy constructor and assignment operator:

Copy and assignment create a copy with the correct data.
Copy and assignment create a deep copy.
Copy and assignment function correctly when the source object is empty.
Assignment protects against self-assignment.

Tests of the edge iterator:

Edge iterator functions correctly when every vertex has one or more neighbors.
Edge iterator functions correctly when one or more vertex has no neighbors; includes the possibility of two or more consecutive vertices having no neighbors.
Dereference and increment throw invalid_argument when applied to an uninitialized iterator.
*egBegin() returns first edge of a non-empty Graph; egBegin() != egEnd() unless the Graph has no edges.

Tests of the neighbor iterator:

Neighbor iterator functions correctly for vertices having one or more neighbors.
Neighbor iterator functions correctly for vertices having no neighbors.
Dereference and increment throw invalid_argument when applied to an uninitialized iterator.
*nbBegin() returns first neighbor of a vertex; nbBegin() != nbEnd() unless the vertex has no neighbors.

What to Submit

You must submit the following files to the proj1 directory.

EntryList.h
EntryList.cpp
Graph.cpp
mytest.cpp

You do not need to submit Graph.h because it should not have changed. If you do happen to place a copy of Graph.h in your submission directory, it will be replaced by a copy of the original version.

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.

cp EntryList.h EntryList.cpp Graph.cpp mytest.cpp ~/cs341proj/proj1/

CMSC 341 Data Structures — Projects & Support — Spring 2020