Project 1: Sparse Adjacency Matrices

Due: Tuesday, February 19, before 9:00 pm

Addenda

IMPORTANT: your m_re array should be initialized to all zeros. This is consistent with the definition of the array in the project description. You do not need special values to indicate that a row is empty: row i is empty if m_re[i] == m_re[i+1]. Initializing with any other value will cause problems with the grading programs.
The sample output files (test1.txt, etc.) did not include the last element of m_re. The files have been updated.
The numEdge() function used to produce the sample output files was returning the number of entries in m_nz and m_ci which is twice the number of edges. The function has been corrected and the output files updated. Because we are only considering graphs without self-edges, the number of entries in m_nz and m_ci will always be twice the number of edges. Be sure that your function returns the correct value.

Objectives

The objective of this programming assignment is to review C++ programming using following features: object-oriented design, dynamic memory allocation, array manipulation, iterators, and exceptions.

Introduction

In computer science and discrete mathematics, a graph is not a plot of y = f(x). A graph has vertices and edges. Here's a simple example:

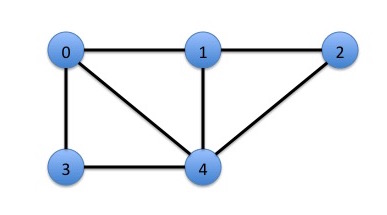
The circles are the vertices and the edges are the lines between the vertices. It is common to use the words "node" and "vertex" interchangeably.

In the example above, the set of vertices is {0,1,2,3,4} and the set of edges is {(3,4), (4,1), (3,0), (0,4), (0,1), (2,1), (4,2)}. It is common to use the ordered pair notation (u, v) to represent an edge, but in an undirected graph, the edges are not ordered. Thus, (2,1) and (1,2) are the same edge.

One common way to store a graph is using an adjacency matrix data structure. This data structure is just a matrix (two-dimensional array) in which the (u, v) entry is one if (u, v) is an edge and zero otherwise. For example, the graph above can be stored as:

The neighbors of a vertex v are the vertices in the graph that are connected to v by an edge. The first row of the matrix A, indexed by 0, indicates that vertex 0 has edges in common with vertices 1, 3, and 4; they are the neighbors of vertex 0.

Note that each edge is represented twice in A. For example, since there is an edge between vertex 0 and vertex 3, there are ones in both the (0, 3) and the (3, 0) entries of A. This is because the graphs we will work with in this project are undirected, meaning that an edge indicates a connection between two vertices without regard to direction.

Many graphs used in applications are sparse, meaning that they have relatively few ones. For example, suppose we wanted to make a graph in which the vertices are all members of the UMBC community (students, faculty, staff) and there is an edge between two vertices if either person has ever sent the other an email. Most of us only have email communication with a very small subset of all the people at UMBC: our rows in the matrix would be mostly zeros. It is a waste of memory to store all those zeros.

So how can we store our adjacency matrix without wasting space? We will use compressed sparse row format. Let N denote the number of vertices in the graph and NNZ the number of non-zero entries in our adjacency matrix. We can store the adjacency matrix efficiently with three arrays:

nz — an integer array of length NNZ storing all the non-zero entries in row-major order. The first elements of nz are the non-zero elememnts of row 0, followed by the non-zero elements of row 1, etc. The data for each row should be stored in order of increasing column index.
re — an integer array of length N+1 indicating where each row's data starts in nz. That is, the data for row u starts at index re[u] of nz. The last element of re should always be equal to NNZ.
ci — an integer array of length NNZ storing the column indices for the elements in nz.

The adjacency matrix A for our example graph would be encoded as follows:

    nz = {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}
    re = {0, 3, 6, 8, 10, 14}
    ci = {1, 3, 4, 0, 2, 4, 1, 4, 0, 4, 0, 1, 2, 3}

Comments:

You may be thinking that there is something wrong with my definition of "efficient" since the sparse encoding stores 33 integer values when the original matrix could be stored with only 25 values. It is true that this is not particularly helpful for small matrices, but it is space efficient when working with large sparse matrices.
Why are we bothering to store values in nz if they will always be ones? The short answer is that they will not necessarily always be ones. Sometimes it is useful to weight the edges of a graph. Going back to the UMBC email example, I might want to record how many emails were sent between individuals, not just the fact that one or more emails were sent; large edge weights might be indicative of which connections are more important.

Assignment

Your assignment is to implement a sparse adjacency matrix data structure Graph that is defined in the header file Graph.h. The Graph class provides two iterators. One iterator produces the neighbors for a given vertex. The second iterator produces each edge of the graph once.

Additionally, you must implement a test program that fully exercises your implementation of the Graph member functions. Place this program in the main() function in a file named Driver.cpp.

The purpose of an iterator is to provide programmers a uniform way to iterate through all items of a data structure using a for loop. For example, using the Graph class, we can iterate thru the neighbors of vertex 4 using:

Graph::NbIterator nit ; for (nit = G.nbBegin(4); nit != G.nbEnd(4) ; nit++) { cout << *nit << " " ; } cout << endl ;

The idea is that nit (for neighbor iterator) starts at the beginning of the data for vertex 4 in nz and is advanced to the next neighbor by the ++ operator. The for loop continues as long as we have not reached the end of the data for vertex 4. We check this by comparing against a special iterator for the end, nbEnd(4). This requires the NbIterator class to implement the ++, != and * (dereference) operators.

Similarly, the Graph class allows us to iterate through all edges of a graph using a for loop like:

Graph::EgIterator eit ; tuple<int,int,int> edge ; for (eit = G.egBegin() ; eit != G.egEnd() ; eit++) { edge = *eit ; // get current edge cout << "(" << get<0>(edge) << ", " << get<1>(edge) << ", " << get<2>(edge) << ") " ; } cout << endl ;

Note that each edge should be printed only once, even though it is represented twice in the sparse adjacency matrix data structure.

Since a program may use many data structures and each data structure might provide one or more iterators, it is common to make the iterator class for a data structure an inner class. Thus, in the code fragments above, nit and eit are declared as Graph::NbIterator and Graph::EgIterator objects, not just NbIterator and EgIterator objects.

If you have not used nested class declarations before, here's an example: nested.cpp and sample output. (For convenience, the class declarations and implementation are provided in one file, contrary to course coding standards.)

Specifications

Here are the specifics of the assignment, including a description for what each member function must accomplish.

Requirement: your implementation must dynamically resize the m_nz and m_ci arrays. See the descriptions of Graph (constructor) and addEdge, below.

Requirement: other than the templated tuple class, you must not use any classes from the Standard Template Library or other sources, including vector and list. All of the data structure must be implemented by your own code.

Requirement: your code must compile with the original Graph.h header file. You are not allowed to make any changes to this file. Yes, this prevents you from having useful helper functions. This is a deliberate limitation of this project. You may have to duplicate some code.

Requirement: per our course coding standards, your code must compile with g++ on the GL servers without using any compilation flags.

Requirement: a program fragment with a for loop that uses your NbIterator must have worst case running time that is proportional to the number of neighbors of the given vertex.

Requirement: a program fragment with a for loop that uses your EgIterator must have worst case running time that is proportional to the number of vertices in the graph plus the number of edges in the graph.

These are the member functions of the Graph class (not including the member functions of the inner classes).

This is the constructor for the Graph class. The Graph class does not have a default constructor, because we want the programmer to specify the number of vertices in the graph using the parameter n. If the n given is zero or negative, throw an out_of_range exception.

The constructor must dynamically allocate space for the three arrays required by the sparse matrix format. The constructor does not know how large the m_nz and m_ci arrays will need to be, but it is reasonable to create them each with n elements; if more space is needed, the arrays will be dynamically resized by the addEdge function (see below).

This is the copy constructor for the Graph class. It should make a complete (deep) copy of the Graph object G given in the parameter. The target of the copy is the host object.

You should not call the assignment operator from the copy constructor (or vice versa). The objective of these two member functions are sufficiently different that you should implement them separately.

This is the overloaded assignment operator for the Graph class. It is called when the compiler sees an assignment like:

where both A and B are Graph objects. The object A becomes the host object of the function and B is passed to the function as rhs.

Remember to check for self-assignment and to free all dynamically allocated data members of the host. You should not use the copy constructor in the implementation of the assignment operator.

This is the destructor for the Graph class. All dynamically allocated memory associated with the host object must be deallocated. You should use valgrind on GL to check for memory leaks.

This function returns the number of vertices in the graph.

This function returns the number of edges in the graph.

This function should add an edge between vertices u and v with weight w. Note that you will need to add entries for both the (u, v) and (v, u) positions of the adjacency matrix. If the value for u or v is invalid, throw an out_of_range exception.

If the m_nz and m_ci arrays are full when addEdge is called, the function must dynamically resize the arrays by creating new arrays with twice the capacity, copying the data from the existing m_nz and m_ci arrays to the new arrays, deleting the old arrays, and assigning the new arrays to the class variables m_nz and m_ci. The function can tell if a resize is necessary by checking the m_cap class variable.

You must not create duplicate edges in the data structure. If addEdge(u, v, w) is called and the edge (u, v) already exists, then the function should just set the weight of the existing edge to w.

This member function is used for debugging. It should print out the number of vertices, number of edges, and current capacity of m_nz (the array of non-zero entries). In adddition, it must print the contents of three arrays m_nz, m_re, and m_ci.

Note: you should not use the neighbor iterator in dump(), because dump() is supposed to help you debug your program when the iterators are not working!

These two functions call the EgIterator constructor to create iterators that can be used in for loops to iterate through the edges of the graph. (See example above.)

These two functions call the NbIterator constructor to create iterators that can be used in for loops to iterate through the neighbors of vertex v. (See example above.)

These are the member functions of the edge iterator class EgIterator:

This is the constructor for the EgIterator class. It is a default constructor, since each parameter has a default value. The constructor should allow an EgIterator to be declared without any arguments.

If called with no arguments, the constructor may leave m_row unitialized since there is no graph associated to the iterator. However, if a pointer to a Graph object is provided in Gptr, the constructor should initialized m_indx to zero (or the value of indx, if specified) and set m_row to the row corresponding to the value of m_indx. Note that it is possible for rows to have no edges, so the correct value of m_row must be computed by the constructor.

This overloaded operator compares two EgIterator objects. It will only be used to compare an EgIterator against the end iterator and must return false when the end is reached. All other uses are unspecified.

The post increment ++ operator should advance the iterator to the next viable edge. The dummy parameter indicates this is a post increment operator and not a preincrement operator. The dummy parameter is not actually used as a parameter.

The ++ operator should have no effect if applied to an iterator that is already at the end.

This is the overloaded dereference operator. It returns a three-tuple (u, v, w) of integers using the tuple class from the standard library where u and v are the source and destiation vertices and w is the edge weight. The tuple returned is the edge that the iterator is currently visiting. Throw an out_of_range exception if the dereference operator is applied to an iterator that has reached the end. See Implementation Notes below for further comments.

These are the member functions of the neighbor iterator class NbIterator. They are analogous to the functions for EgIterator.

This is the constructor for the NbIterator class. It is a default constructor, since each parameter has a default value. The constructor should allow an NbIterator to be declared without any arguments.

The parameter v specifies that we wish to iterate over the neighbors of vertex v. The class variable m_nrow should be initialized to the value of v.

A value of indx may be provided, in which case m_indx should be set to the value of indx; this would typically only be done to create an nbEnd iterator.

If a pointer to a Graph object is provided in Gptr, the constructor should initialize m_row to the value of v and m_indx to the index of the first element of row m_row in the m_nz array.
As before, the only intended use of the != operator is to compare an NbIterator object against the end iterator.
The ++ operator advances the iterator to the next neighbor of m_row. All neighbors are viable, so this ++ operator should be simpler to implement than the one for EgIterator.

The ++ operator should have no effect if applied to an iterator that is already at the end.
This dereference operator should return the neighbor that the iterator is currently visiting. Throw an out_of_range exception if the dereference operator is applied to an iterator that has reached the end.

Test Programs

The following test programs may be used to check the compatibility of your implementation. These programs do not check the correctness of your implementation. Even if your implementation compiles and runs correctly with these programs, it does not mean your implementation is error-free. Grading will be done using programs that exercise your implementation much more thoroughly. You must do the testing yourself --- testing is part of programming. Conversely, if your implementation does not compile or does not run correctly with these test programs, then it is unlikely that it will compile or run correctly with the grading programs.

test1.cpp
test1.txt (sample output)
test1v.txt (sample output with valgrind)
test2.cpp
test2.txt (sample output)
test2v.txt (sample output with valgrind)

These files, as well as Graph.h, are also available on GL in the directory:

/afs/umbc.edu/users/c/m/cmarron/pub/www/cs341.s19/projects/proj1files/

Implementation Notes

Approach this assignment using incremental development. Implement the Graph constructor, addEdge() and dump() functions first. Then write a driver program that creates a graph, adds a few edges and calls dump(). When you have debugged these functions, implement the NbIterator class (it's easier). When you have those functions fully debugged, then implement the EgIterator class.
The EgIterator and NbIterator classes do not need destructors, copy constructors, or overloaded assignment operators because they do not have any dynamically allocated data members. The compiler supplied destructor, copy constructor, and assignment operator will do the right thing.
Graphs are allowed to have vertices that do not have any edges. The EgIterator constructor should work correctly even if vertex 0, 1, 2 ... have no edges. Similarly, the ++ operator for the EgIterator should be able to handle vertices with no edges.
If you are still confused about what an iterator is supposed to do, consider this implementation of the dereference operator for NbIterator:

The purpose of the iterator is to give a programmer using the Graph class access to the neighbors of a vertex. The dereference operator is where the rubber meets the road. When you dereference the iterator, you get an actual neighbor vertex. That means the iterator should always be in a state where dereferencing gives you the current neighbor vertex (unless you have reached the end). That tells you what nbBegin() and the ++ operator has to do. The nbBegin() object must set m_indx to the index of the first neighbor. The ++ operator must advance the iterator to the next neighbor.

The dereference operator for the EgIterator is similar. For the dereference operator to work, the EgIterator member functions and operators must set the m_indx and m_row data members correctly.
The reason that egBegin() and nbBegin() are members of Graph rather than the iterator classes is that the iterators have to be told which graph they are working with. Since egBegin() and nbBegin() are members of Graph, they can give their host pointers (the this pointer) to the iterator constructors.
The "normal" iterator constructors (not creating the end iterator or the empty iterator) should create an iterator compatible with egBegin() and nbBegin().
Test your programs for memory leaks (dynamically allocated memory that was never released) using valgrind. The valgrind command is available on GL. Just compile your test program and run:
This is assuming that your executable file is named Driver.out. If that run did not leak memory, the output from valgrind will say: As usual, the fact that a single run of your implementation did not leak memory does not mean that it will never leak memory.

What to Submit

You must submit the following files to the proj1 directory.

Graph.cpp
Driver.cpp

You do not need to submit Graph.h because it should not have changed. If you do happen to place a copy of Graph.h in your submission directory, it will be replaced by a copy of the original version.

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.

cp Graph.cpp Driver.cpp ~/cs341proj/proj1/

CMSC 341 Data Structures — All Sections — Spring 2019