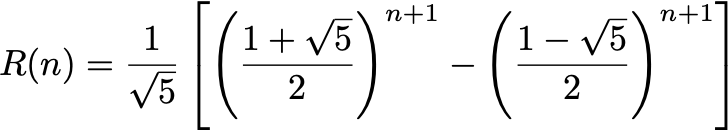Homework 4: Induction

Due: Thursday, April 18, before 9:00 pm

Instructions: Your solutions to the following problems must be typed, converted to PDF, and submitted on Blackboard. It is okay to discuss concepts underlying the problems with other students, but all final solutions must be your own work.

All solutions must be typed, converted to PDF, and submitted on Blackboard. No other format is acceptable. Scans or photos of hand-written solutions will not be accepted.

All of the following problems require proof by induction. A complete proof should be clearly written, including descriptive text (not just symbols), and must include the following:

Exercise #1: (5 points) Define the sequence an by

Prove by induction that an < (7/4)n for all n≥1.

Exercise #2: (5 points) Prove by induction: x2n - 1 is divisible by x - 1 for all n≥0.

Exercise #3: (5 points) We frequently use the formula for the sum of the first n positive integers. Less commonly used is the formula for the sum of the squares of the first n positive integers:

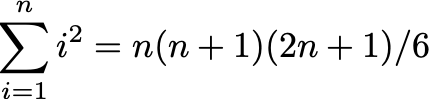
Prove by induction that this formula is correct for n ≥ 1.

Exercise #4: (6 points) The king in chess can move to any neighboring square horizontally, vertically, or diagonally. Suppose that a king starts on an infinite chess board. Let S(n) denote the number of different squares the king can be in after n moves. For example, S(1) = 8 since in a single move the king can only reach the eight squares adjoining the starting square.

Prove by induction: S(n) = (2n + 1)2 for n > 1.

Exercise #5: (9 points) A newborn pair of rabbits (one male, one female) is placed in a large enclosed pen. Rabbit pairs are not fertile during their first month of life, but give birth to one new male/female pair at the end of the second month and every month thereafter. How many pairs of rabbits will there be after n months, n ≥ 0?

To solve this problem, first derive a recurrence relation for R(n), the number of pairs of rabbits after n months. Then prove by induction that R(n) satisfies