Project 3, Lazy Binary Search Trees

Due: Tuesday, April 11, 8:59pm

Addenda

Corrections/clarifications in orange below.

Objectives

The objective of this programming assignment is to have you practice using recursion in your programs and to familiarize you with the binary search tree data structure.

Introduction

In real life, laziness if often disdained. (See Wikipedia article on sloth.) In computer science, however, laziness is sometimes a viable strategy. Why do today what you can put off until tomorrow? especially if there is a chance that you won't actually have to do it tomorrow either?

In contrast to a AVL trees and Red-Black Trees, where we diligently maintain a balance condition to guarantee that the tree has O( log n) height, in a Lazy BST, we don't worry about the balancing until things get really out of whack. Insert and delete proceed in the same manner as an unbalanced binary search tree until we notice that at some node of the BST, the left subtree is twice as large as the right subtree (or vice versa). When this happens we rebalance the subtree of the Lazy BST rooted at this node.

When a subtree of a Lazy BST is rebalanced, we convert the entire subtree into a sorted array. Then we convert the array back into a perfectly balanced BST. Rebuilding is easy because the array is sorted. We can find the middle element of the array in constant time and make it the root of the new subtree. Then, we recursively build the left subtree and the right subtree using, respectively, the portion of the array that has keys smaller than the root and the portion of the array that has keys larger than the root. The result is a binary search tree that is as balanced as possible. (See Project 3 Examples.) The rebalance procedure takes O( t ) on a BST subtree with t elements. However, we don't have to rebalance very often — amortized analysis shows that the insert and delete procedures take O( log n ) amortized time on a Lazy BST with n elements.

Since rebalancing is expensive, we add another provision: we won't rebalance a subtree that has height ≤ 3. An unbalanced subtree that has height 3 will not add very much to the height of the overall tree and hence will not contribute very much to the running time of the BST procedures. (We adopt the convention that the height of a leaf to is 0, where a leaf is a node that has actual data and no children.) By ignoring small unbalanced subtrees, we can avoid excessive rebalancing.

One note about the rebalance procedure: it is possible for a Lazy BST to have two nodes x and y where rebalancing is needed where x is an ancestor of y. In this situation, we want to do the rebalancing at x since rebalancing the subtree rooted at x will also rebalance the subtree rooted at y. If we rebalanced at y first, the time spent rebalancing at y is completely wasted since all that work is undone when we rebalance at x. (See Project 3 Examples.)

Assignment

Note: Running time is one of the most important considerations in the implementation of a data structure. Programs that produce the desired output but exceed the required running times are considered wrong implementations and will receive substantial deductions during grading.

Your assignment is to implement a Lazy BST. You may start with a binary search tree class from the textbook or given by your instructor, if you prefer. You may also design your own. Each option has advantages and disadvantages. A primary objective of this programming assignment is to have you use recursion. So, one component of grading will evaluate how elegantly you employ recursion to implement this data structure. (Yes, you are being graded on aesthetics!)

Since you will choose the design of the class definitions, no header files will be distributed with this project. Instead, the requirements are:

In order to implement LazyBST efficiently, your data structure must be able to determine the size and height of a subtree in constant time. You must have data members for the height and size of a subtree in the class representing the root of a subtree of a Lazy BST. The height and size data members must be updated whenever the height or size of that subtree changes. The update must not affect the asymptotic running time of insert, delete and search. These must still run in time proportional to the height of the tree.

To keep things simple for this project, we will just store int values in LazyBST. Although, well-written code should allow you to easily change the type of data stored in the data structure.

Here are the member functions you must implement in your LazyBST class. (You will need to implement others for your own coding needs.)

  1. A default constructor with the signature 

       LazyBST::LazyBST() ;

    The default constructor must create a LazyBST object that is ready to have its member function invoked without any further processing.

  2. A copy constructor with the signature 

       LazyBST::LazyBST(const LazyBST& other) ;

    The copy constructor must make a deep copy and create a new object that has its own allocated memory.

  3. A destructor with the signature 

       LazyBST::~LazyBST() ;

    The destructor must completely free all memory allocated for the object. (Use valgrind on GL to check for memory leaks.)

  4. An overloaded assignment operator with the signature: 

       const LazyBST& LazyBST::operator=(const LazyBST& rhs) ;

    The assignment operator must deallocate memory used by the host object and then make deep copy of rhs.

  5. An insert() function that adds an item to LazyBST that has the following signature: 

       void LazyBST::insert (int key) ;

    The insert() function must run in time proportional to the height of the Lazy BST (not counting time for rebalancing). Your LazyBST implementation must not allow duplicates. If the insert() function is invoked with a key value that already stored in the Lazy BST, your insert() function should do nothing, except that it may rebalance the tree if an imbalance is detected.

  6. A remove() member function that finds and removes an item with the given key value. The remove() function should return a boolean value that indicates whether the key was found. Your remove() function should not abort or throw an exception when the key is not stored in the BST. The remove() member function must have the following signature: 

       bool LazyBST::remove(int key) ;

    For full credit, your remove() method must run in time proportional to the height of the tree (not counting time for rebalancing).

  7. A find() function that reports whether the given key is stored in the tree. The signature of the find() method should be: 

       bool LazyBST::find(int key) ;

    For full credit, your find() method must run in time proportional to the height of the tree.

  8. A member function rebalance() that rebalances a subtree of the Lazy BST as described above. The running time of rebalance() must be proportional to the number of nodes in the subtree being rebalanced. Note that a proper implementation would require you the keep track of the size and height of the subtree. Read the description above.

  9. A member function inorder() that performs an inorder walk of the LazyBST and at each node, prints out the key followed by a : followed by the height of the node followed by another : followed by the size of the subtree rooted at that node. Furthermore, inorder() should print an open parenthesis before visiting the left subtree and a close parenthesis after visiting the right subtree. Nothing should be printed when inorder() is called on an empty tree, not even parentheses. This function will be used for grading, so make sure that it works correctly. The function must have the following signature: 

       void LazyBST::inorder() ;

    For example, calling inorder() on the following BST should produce the string:

    (((((3:0:1)7:2:4((9:0:1)11:1:2))14:3:8((15:1:2(17:0:1))20:2:3))22:4:13(((24:0:1)26:1:2)30:2:4(37:0:1)))41:5:22((((50:0:1)54:1:3(59:0:1))60:2:4)64:3:8((71:1:2(75:0:1))79:2:3)))

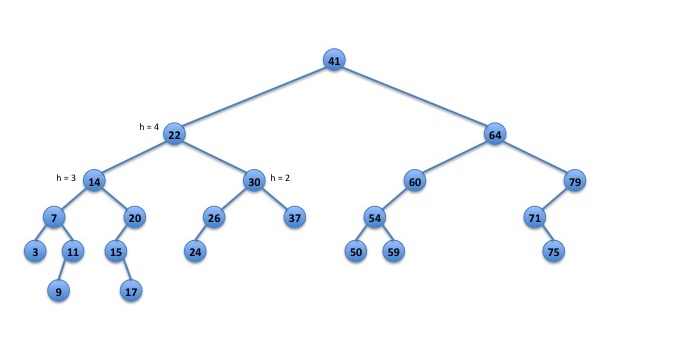
    Fig. 1: an unbalanced binary search tree.

    Here, the 41:5:22 indicates that the node with key 41 has height 5 and that there are 22 nodes in the tree. The output before 41:5:22 is produced by visiting the left subtree. Everything after 41:5:22 is produced by visiting the right subtree.

  10. A function locate() that returns whether there is a node in a position of the LazyBST and stores the key in the reference parameter. The position is given by a constant C string, where a character 'L' indicates left and a character 'R' indicates right. The locate() function must have the signature 

       bool LazyBST::locate(const char *position, int& key) ;

    For example in the BST above:
    • A call to locate("LRL",key) should return true and store 26 in key.
    • A call to locate("RRLR",key) should return true and store 75 in key.
    • A call to locate("RLR",key) should return false and not make any changes to key since there is not a node in that position. Note: locate() must not abort and must not throw an exception in this situation.
    • A call to locate("",key) should return true and store 41 in key, since the empty string indicates the root of tree.
    The grading programs will use locate() to check if your BST is balanced and that the keys are stored correctly. So, make sure locate() is correct. (This is not a difficult function to implement.)

Your code must run without segmentation fault and without memory leaks. For grading purposes, memory leaks are considered as bad as segmentation faults. This is because many segmentation faults are cause by poorly written destructors. A program with an empty destructor might avoid some segmentation faults but will leak memory horribly. Thus, not implementing a destructor or not deleting unused memory must incur a penalty that is equivalent to a segmentation fault.

Test Programs

Here are sample driver programs to test your implementation. Passing these tests do not mean you will receive 100% on your project. It does not guarantee that you will pass tests used in grading. You should make additional tests of your own!

Note: your output may differ from the sample out provided because you may have correctly implemented remove() and rebalance() differently.

Implementation Notes

Here we list some recommendations and point out some traps and pitfalls.

What to Submit

You must submit the following files to the proj3 directory.

The Driver.cpp program should include tests showing the parts of your project that work correctly.

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.

cp LazyBST.h LazyBST.cpp Driver.cpp ~/cs341proj/proj3/