Project 3, An Experimental Binary Search Tree

Due: Tuesday, October 31 November 7, 8:59pm

Addenda

Corrections/clarifications in orange below.

Objectives

The objective of this programming assignment is to have you practice using recursion in your programs and to familiarize you with the binary search tree data structure.

Introduction

If you never learned about AVL Trees and Red-Black Trees, would you be able to design a balanced binary search tree? AVL Trees and Red-Black Trees are rather intricate data structures. All the cases fit together rather nicely and the rotations work just right. Sometimes we are awed by such data structures, we tend to think that there is no way we would even begin to suspect that such a data structure is possible, let alone design one ourselves.

In this project we will experiment with binary search trees and, hopefully, convince you that maybe you could have been the one to design the first balanced binary search trees, if only you were born 60 or 70 years earlier.

Now let's think about AVL Trees and Red Black Trees for a moment. Basically there are two steps in the algorithm. First, there is some way to determine that the tree is "unbalanced". In AVL Trees, this is when the height of the left and right subtrees differ by more than 1. In Red-Black trees, the coloring requirements might be messed up. In the second step, we rearrange the top few levels of the subtree that is unbalanced. Note that in both AVL Trees and Red-Black Trees, only the top few levels of the subtree is rearranged, no matter if the tree has height 10 or height 100.

Now let us devise a very simple scheme to determine if a subtree is unbalanced. Let us say that a subtree is unbalanced if the height of the subtree is more than 2 log m where m is the number of nodes in that subtree. For example, consider the subtree depicted below:

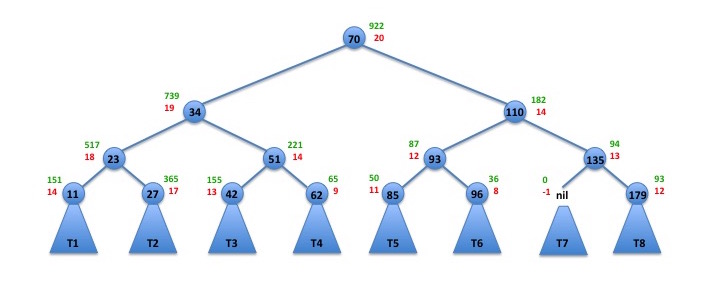
The numbers in green are the sizes of the subtrees — the number of nodes in that subtree. The numbers in red are the heights of the subtrees. For example, the node with key 34 has height 19 and size 739. Note that since 2 log(739) ≈ 19.058, that subtree is not "unbalanced". On the other hand, the root of this tree is unbalanced because 2 log(922) ≈ 19.697 and the tree has height 20. You can verify for yourself that the other nodes in the tree are not unbalanced.

So, what can we do? Well, we can rearrange the tree and make 51 the new root (see figure below), but that doesn't help because the tree still has height 20.

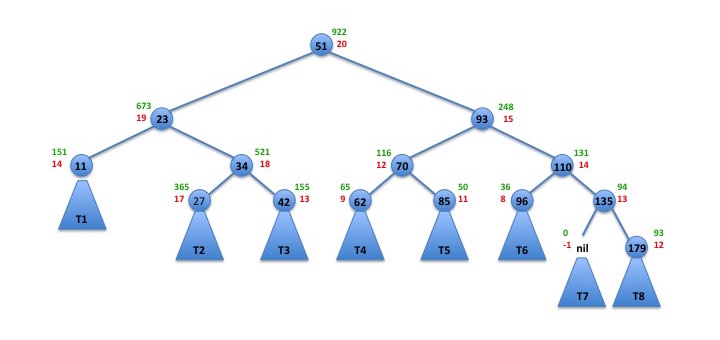
On the other hand, if we made 34 the new root, we could rearrange the tree and get a new tree with height 19. Then, the tree would be balanced according to our current definition of "balanced".

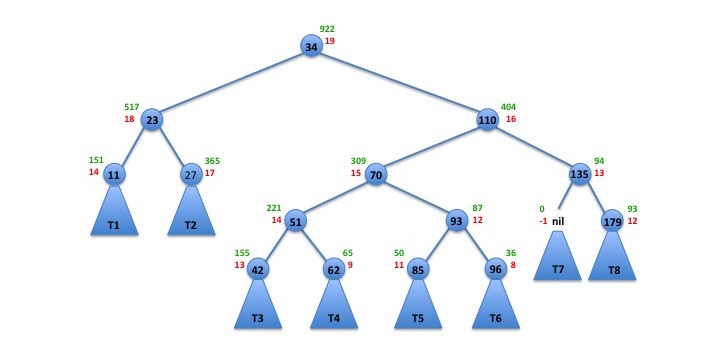
But how would we know to pick 34 as the new root? Easy, we try "everything". Starting with the original tree that has 70 as the root, we can perform a truncated inorder walk up to depth 3. (In our definition of depth, the root 70 has depth 0, its children have depth 1, ... so a node like 27 has depth 3.) The truncated inorder walk will give us a list of subtrees and "singleton" nodes, which we can place in an array:

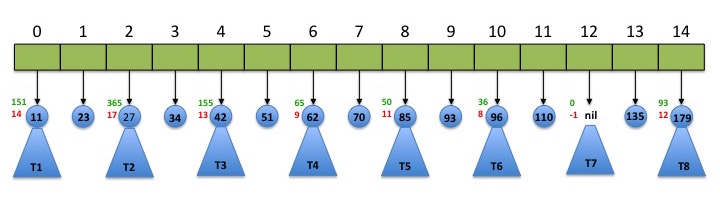
Note that we want to include the empty tree that is the left child of 135 in the array. This allows us to claim that the singleton nodes are always in odd indexed positions in the array and that the subtrees are at even indices. To transform this array of subtrees and singleton nodes back into a binary search tree, we can use any singleton node as the new root. For example, if we picked 93 to be the new root, then its left subtree will include the keys from T1, 23, T2, 34, T3, 51, T4, 70, T5 and its right subtree will include T6, 110, T7, 135, T8. To find the best root, we try all the singleton nodes as potential roots of the new tree and pick one that will give us the shortest tree.

But how do we determine the height of the shortest tree that has say 34 as the root? Well, in order to have a shortest tree, the left subtree must be arranged optimally and the right subtree must also be arranged optimally. How do we do that? recursively. If we picked 34 to be the new root, there is only one way to arrange T1, 23, T2 into a binary search tree: 23 must be the root of the left subtree. The right subtree of 34 would include T3, 51, T4, 70, T5, 93, T6, 110, T7, 135, T8. This time, there are many ways to construct a subtree. If we reconstructed the right subtree optimally, then we would discover that it is best to pick 70 as the root of the right subtree. We would have discovered this recursively, by trying all of the singleton nodes, 51, 70, 93, 110 and 135, as roots of the right subtree and figuring out that 70 gives the shortest right subtree.

Ordinarily, such an exhaustive search for the optimal root will result in an exponential time algorithm. However, we will only take apart our binary search tree down to a fixed depth. If we limit ourselves to depth 3, then there can be at most 16 items in the array of subtrees and singleton nodes. Exhaustive search on 16 items will be constant time. (In CMSC 441 Algorithms, you will study dynamic programming which can be used to reduce the running time of this step.)

So here is our strategy: we will store at each node of the binary search tree, the size and height of the subtree rooted at that node. Whenever we add an item to or remove an item from the binary search tree, we examine all of the nodes on the path from the root to where a node was inserted or deleted. At those nodes, we check that the height is no more than 2 log(size). This should be checked when we return from the recursive calls to insert or delete. Note that in delete, we consider the path from the root to the node that was actually removed from the tree. This node might not hold the key that was deleted, because in the case where we want to remove a node that has two children, we actually remove the node that has the highest key in the left subtree. It is this node in the left subtree that has been "removed" from the tree. Checking and updating the height and size at each node on this path should take constant time per node examined.

Now, suppose we find an unbalanced node. Then we break apart the subtree rooted at that node down 3 levels and store the singleton nodes and subtrees in an array. Finally, we reconstruct the subtree by exhaustively and recursively determine the best singleton node to have as the root of the rearranged subtree.

Will this work? Are we guaranteed to have a tree with 2 log n height? We don't know because:

  1. We don't know that reconstructing tree in this way will reduce the height of the tree. It might be the case that we reconstruct the tree optimally and the height remains the same. In this situation we say that the rebalance has failed.
  2. We also don't know that reducing the height will necessarily produce a tree with height less than 2 log m.

(BTW, this is why AVL Trees and Red-Black Trees need proofs to show that their rebalancing scheme works.)

Even though we do not have a guarantee that our rebalancing scheme works, we can still try the algorithm experimentally and see how well it works. Also, there is no particular reason to use 2 log m as definition of unbalanced. Maybe a different factor other than 2 would work better. Again, there's no particular reason for us to break apart a subtree only down to depth 3. We can try different depths to see what works better in terms of running times and in terms of getting a shorter binary search tree. In this project, we will also tune these two parameters.

Assignment

Note: Running time is one of the most important considerations in the implementation of a data structure. Programs that produce the desired output but exceed the required running times are considered wrong implementations and will receive substantial deductions during grading.

Your assignment is to implement the Experimental BST described above. You may start with a binary search tree class from the textbook or given by your instructor, if you prefer. You may also design your own. Each option has advantages and disadvantages. A primary objective of this programming assignment is to have you use recursion. So, one component of grading will evaluate how elegantly you employ recursion to implement this data structure. (Yes, you are being graded on aesthetics!)

Since you will choose the design of the class definitions, no header files will be distributed with this project. Instead, the requirements are:

In order to implement ExpBST efficiently, your data structure must be able to determine the size and height of a subtree in constant time. You must have data members for the height and size of a subtree in the class representing the root of a subtree of a ExpBST. The height and size data members must be updated whenever the height or size of that subtree changes. The update must not affect the asymptotic running time of insert, delete and search. These must still run in time proportional to the height of the tree.

To keep things simple for this project, we will just store int values in ExpBST. Although, well-written code should allow you to easily change the type of data stored in the data structure.

Here are the member functions you must implement in your ExpBST class. (You will need to implement others for your own coding needs.)

  1. A default constructor with the signature 

       ExpBST::ExpBST() ;

    We would usually use the next constructor to create an ExpBST object. However, a class without a default constructor can be problematic, so we will include a default constructor.

  2. A constructor with the signature 

       ExpBST::ExpBST(int depth, int minHeight, float factor) ;

    Here depth specifies the maximum depth taken by the truncated inorder walk when we take apart an ExpBST during the rebalancing operation. Recall that the root has depth 0, the children of the root have depth 1. The parameter minHeight indicates the height of the shortest tree that will be considered for rebalancing. For example, if minHeight is 5, then we will not rebalance subtrees of height 4, 3, 2, 1 or 0. Finally, factor is the multiple of log m we use to define when a subtree is unbalanced. For example, if factor is 2.0 then a subtree with m nodes and height greater than 2.0 log m is unbalanced. Note that factor is allowed to have fractional values.

    For simplicity, you may store these values in static data members. This does mean that a program can only have ExpBST trees of the same type. Otherwise, these values would have to be associated with the root of the tree, and the root would have to be distinguished from other nodes in the tree.

  3. Your ExpBST class must also have the following functions that return the values passed to the constructor above. 

       int getMaxRebalanceDepth() const  ;  
   int getMinRebalanceHeight() const ;
   float getRebalanceFactor() const ;

  4. A copy constructor with the signature 

       ExpBST::ExpBST(const ExpBST& other) ;

    The copy constructor must make a deep copy and create a new object that has its own allocated memory.

  5. A destructor with the signature 

       ExpBST::~ExpBST() ;

    The destructor must completely free all memory allocated for the object. (Use valgrind on GL to check for memory leaks.)

  6. An overloaded assignment operator with the signature: 

       const ExpBST& ExpBST::operator=(const ExpBST& rhs) ;

    The assignment operator must deallocate memory used by the host object and then make deep copy of rhs.

  7. An insert() function that adds an item to ExpBST that has the following signature: 

       void ExpBST::insert (int key) ;

    The insert() function must run in time proportional to the height of the ExpBST. Your ExpBST implementation must not allow duplicates. If the insert() function is invoked with a key value that already stored in the ExpBST, your insert() function should do nothing, except that it may rebalance the tree if an imbalance is detected.

  8. A remove() member function that finds and removes an item with the given key value. The remove() function should return a boolean value that indicates whether the key was found. Your remove() function should not abort or throw an exception when the key is not stored in the BST. The remove() member function must have the following signature: 

       bool ExpBST::remove(int key) ;

    For full credit, your remove() method must run in time proportional to the height of the tree.

  9. A find() function that reports whether the given key is stored in the tree. The signature of the find() method should be: 

       bool ExpBST::find(int key) ;

    For full credit, your find() method must run in time proportional to the height of the tree.

  10. A member function rebalance() that rebalances a subtree of the ExpBST as described above. The running time of rebalance() must be constant. Note that a proper implementation would require you the keep track of the size and height of the subtree. Read the description above.

  11. Your ExpBST class must have the following functions report on statistics of the ExpBST tree related to the rebalance operation: 

       int ExpBST::getNumRebalance() const ;
   int ExpBST::getFailedRebalance() const ;
   int ExpBST::getExceedsHeight() const ;
   void ExpBST::resetStats() ;

    The function getNumRebalance() must return the total number of calls to rebalance() since the beginning of the program or since the last call to resetStats() whichever one is later. Similarly, getFailedRebalance() must return the total number of calls to rebalance() that did not result in a shorter subtree, and getExceedsHeight() must return the total number of calls to rebalance() that resulted in a subtree that is still "too tall" as defined by the factor parameter given to the constructor. Finally, resetStats() will reset these 3 counts to zero.

    As before, for the sake of simplicity, you may store these three counts in static data members, even though this may not be the most correct object-oriented design.

  12. A member function inorder() that performs an inorder walk of the ExpBST and at each node, prints out the key followed by a : followed by the height of the node followed by another : followed by the size of the subtree rooted at that node. Furthermore, inorder() should print an open parenthesis before visiting the left subtree and a close parenthesis after visiting the right subtree. Nothing should be printed when inorder() is called on an empty tree, not even parentheses. This function will be used for grading, so make sure that it works correctly. The function must have the following signature: 

       void ExpBST::inorder() ;

    For example, calling inorder() on the following BST should produce the string:

    (((((3:0:1)7:2:4((9:0:1)11:1:2))14:3:8((15:1:2(17:0:1))20:2:3))22:4:13(((24:0:1)26:1:2)30:2:4(37:0:1)))41:5:22((((50:0:1)54:1:3(59:0:1))60:2:4)64:3:8((71:1:2(75:0:1))79:2:3)))

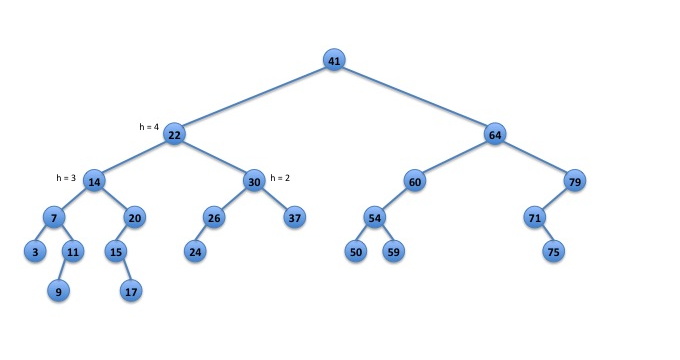
    Fig. 1: an unbalanced binary search tree.

    Here, the 41:5:22 indicates that the node with key 41 has height 5 and that there are 22 nodes in the tree. The output before 41:5:22 is produced by visiting the left subtree. Everything after 41:5:22 is produced by visiting the right subtree.

  13. A function locate() that returns whether there is a node in a position of the ExpBST and stores the key in the reference parameter. The position is given by a constant C string, where a character 'L' indicates left and a character 'R' indicates right. The locate() function must have the signature 

       bool ExpBST::locate(const char *position, int& key) ;

    For example in the BST above:
    • A call to locate("LRL",key) should return true and store 26 in key.
    • A call to locate("RRLR",key) should return true and store 75 in key.
    • A call to locate("RLR",key) should return false and not make any changes to key since there is not a node in that position. Note: locate() must not abort and must not throw an exception in this situation.
    • A call to locate("",key) should return true and store 41 in key, since the empty string indicates the root of tree.
    The grading programs will use locate() to check if your BST is balanced and that the keys are stored correctly. So, make sure locate() is correct. (This is not a difficult function to implement.)

  14. Your ExpBST class must have the following functions to report on attributes of the ExpBST tree: 

       bool ExpBST::empty() const  ;    // tree has no nodes
   int  ExpBST::height() const ;    // height of tree
   int  ExpBST::size() const ;      // number of nodes in tree

    Since the height and size of each subtree is stored at each node, these functions must run in O(1) time.

Your code must run without segmentation fault and without memory leaks. For grading purposes, memory leaks are considered as bad as segmentation faults. This is because many segmentation faults are caused by poorly written destructors. A program with an empty destructor might avoid some segmentation faults but will leak memory horribly. Thus, not implementing a destructor or not deleting unused memory must incur a penalty that is equivalent to a segmentation fault.

Testing

Here are sample driver programs to test your implementation. Passing these tests do not mean you will receive 100% on your project. It does not guarantee that you will pass tests used in grading. You should make additional tests of your own!

Note: your output may differ from the sample out provided because you may have correctly implemented remove() and rebalance() differently.

Tuning Exercise

Use p3test8.cpp to tune your implementation. Run these programs with 100,000 repetitions with different values for the depth, minimum height and factor. Time you runs using the Unix time command and select the combination of values that minimize the running time. Remember that factor is a floating point value and you can select non-integer values like 2.3 for factor. Note the number of failed rebalances and the number of rebalances that exceed the height restriction. Does this matter? Now try your settings on p3test9.cpp and on other sizes. What is your recommendation for values for depth, minimum height and factor?

Remember to show runs of p3test8.cpp and p3test9.cpp in your typescript file when you submit.

Implementation Notes

Here we list some recommendations and point out some traps and pitfalls.

What to Submit

Before submitting, remove all extraneous output from your program. (Just comment them out.) Your typescript file should have only a few hundred lines of output, not 195 megabytes of text. (Yes, that's the record.) We will not look at the typescript file beyond the first 1000 lines.

You must submit the following files to the proj3 directory.

The Driver.cpp program should include tests showing the parts of your project that work correctly. All of your implementation should be placed in ExpBST.h and ExpBST.cpp. Do not submit other files.

If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command command.

cp ExpBST.h ExpBST.cpp Driver.cpp ~/cs341proj/proj3/

Your code should compile with the test programs using these Unix commands on GL:

g++ -I . ../../00Proj3/p3test1.cpp ExpBST.cpp -o t1.out g++ -I . ../../00Proj3/p3test2.cpp ExpBST.cpp -o t2.out g++ -I . ../../00Proj3/p3test3.cpp ExpBST.cpp -o t3.out g++ -I . ../../00Proj3/p3test4.cpp ExpBST.cpp -o t4.out g++ -I . ../../00Proj3/p3test5.cpp ExpBST.cpp -o t5.out g++ -I . ../../00Proj3/p3test6.cpp ExpBST.cpp -o t6.out g++ -I . ../../00Proj3/p3test7.cpp ExpBST.cpp -o t7.out g++ -I . ../../00Proj3/p3test8.cpp ExpBST.cpp -o t8.out g++ -I . ../../00Proj3/p3test9.cpp ExpBST.cpp -o t9.out

Use the Unix script command to record yourself compiling these programs. Then, use p3test8.cpp and p3test9.cpp to perform some timing runs: time ./p3test8.out 100000 3 5 2.0 time ./p3test8.out 200000 3 5 2.0 time ./p3test8.out 400000 3 5 2.0 time ./p3test9.out 100000 3 5 2.0 time ./p3test9.out 200000 3 5 2.0 time ./p3test9.out 400000 3 5 2.0

Finally, run p3test8.cpp and p3test9.cpp using the values of depth, minimum height and factor that you recommend in the tuning exercise.

Finally, remember to exit from script.