Project 2, Square Lists

Due: Tuesday, October 10, 8:59:59pm

Links: [Project Submission] [Late Submissions] [Project Grading] [Grading Guidelines] [Academic Conduct]

Change Log

Modified items are in orange.

[Sunday October 8, 12:45pm] Added 

   -include ../../00Proj2/Int341.h
to the g++ command. This is an attempt to prevent people who do not follow instructions and put a modified copy of Int341.h in their submission directory from hurting themselves too badly. Their copy of Int341.h will be ignored or they might get a compilation error. This is still not 100% foolproof. It is best not to copy Int341.h to the submission directory and, in any case, do not modify Int341.h. We will delete any copies of Int341.h that you submit prior to grading. So, if your program depends on a modified Int341.h to compile, it will not compile when we grade your submission.

[Wednesday October 4, 10:45am] Changed instructions for compiling and running the project to include logging into the "fedora" machines.

[Thursday Sep 28, 08:30am] Changed inspector() function in p2comptest.cpp to be more lenient in the definition of when an inner list is "too long" or "too short". Also, added test for indexOf() function and provided sample output p2comptest.txt

[Tuesday Sep 26, 10:30am] Added sections "Testing", "How to Submit" and "A Note on Timing".

[Tuesday Sep 26, 9:30am] If the position given to SqList::add() is equal to the number of items in the SqList then the data should be added at the end of the SqList.

Objectives

The objective of this programming assignment is to have you practice implementing a new data structure and also to gain some experience using the list template container class from the C++ Standard Template Library (STL).

Introduction

For this project, you will implement a square list data structure. A square list is a linked list of linked lists where each linked list is guaranteed to have O(√n) items:

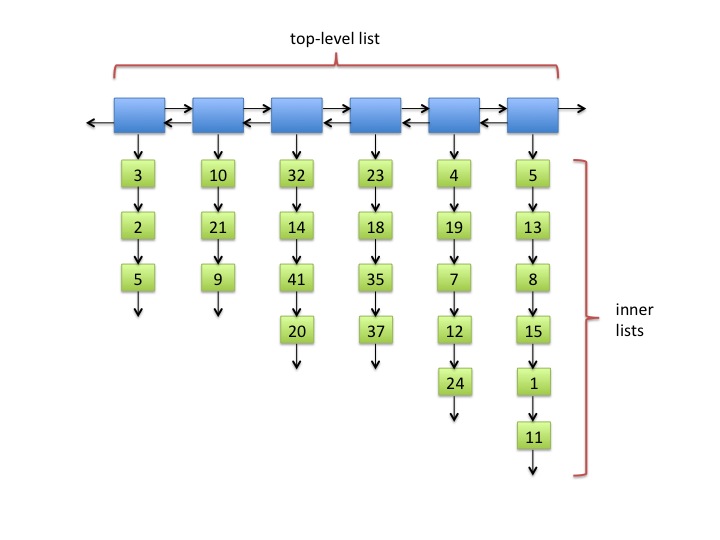
Fig. 1: A typical square list.

Figure 1 shows a typical square list of 25 integer values. The positions of the items are important. The ordering of the items in this example is: 3, 2, 5, 10, 21, 9, 32, 14, 41, 20, 23, ..., 15, 1, 11.

The idea of a square list is that we want to keep the length of the top-level and of all the inner lists bounded by O(√n). That way we can find the ith item of the list in O(√n) time. For example, if we want to find the 9th item in the list, we can progress down the top-level list and check the length of the inner lists. We know the 9th item cannot be in the first inner list, since it only has 3 items. It also cannot be in the second inner list, since the first two lists combined only has 6 items. Instead, we can find the 9th item of the square list by looking for the 3rd item of the third inner list, which turns out to be 41.

To accomplish this search in O(√n) time, we must be able to determine the length of each inner list in O(1) time. In the worst case, we have to search through O(√n) items of the top-level list before we find the inner list that holds the ith item. An additional O(√n) steps will allow us to find the desired item in that inner list, since the length of each inner list is also O(√n).

The main difficulty in maintaining a square list is that as we add items to and remove items from a square list, the length of the inner lists can change. This can happen in two ways. First, obviously, when we add items to or remove items from an inner list, the length of that inner list changes. Secondly, the length of an inner list relative to O(√n) can also change when we add or remove items elsewhere in the square list because doing so changes the value of n. For example, the 5th inner list in Figure 1 has 5 items. This happens to be exactly √25. If we removed all 10 items from the first 3 inner lists, that would leave us with only 15 items in the entire square list. After the removals, the length of the last inner list becomes bigger than √n even though the length of that list didn't change. The length becomes bigger than √n because √n dropped from √25 to √15, and 5 > √15.

Square List Maintenance

Our goal is to make sure that the top-level list and all the inner lists have lengths bounded by O(√n). It is too expensive to require that our square list always has √n inner lists, each with √n items. Instead, we maintain the following two conditions:

Condition 1:
Every inner list has ≤ 2 √n items.
Condition 2:
There are no adjacent short inner lists, where short is defined as having ≤ √n/2 items.

Notice that neither condition says anything about the length of the top-level list. Instead, we claim that if Condition 2 holds, then the top-level list cannot have more than 4 √n items. Too see this, suppose the contrary. That is, suppose that the top-level list has more than 4 √n items. (Yes, this is the beginning of a proof by contradiction.) Then, there must be more than 2 √n inner lists that are not short (otherwise, two of the short inner lists would be adjacent). Thus, the total number of items in these non-short lists must exceed 2 √n × √n/2 = n. This is a contradiction because n is the number of items (by definition) and cannot exceed itself. Therefore, the number of inner lists (and thus the length of the top-level list) must be bounded by 4 √n.

These observations allow us to maintain the O(√n) bounds on the lengths of the top-level list and the inner lists using the following procedure:

Consolidate:

  1. Traverse the top-level list.
  2. Whenever an empty inner list is encountered, remove that inner list.
  3. Whenever two adjacent short inner lists are encountered, merge them into a single inner list. (See Figures 2 and 3.)
  4. Whenever an inner list is found to have more than 2 √n items, split them into two lists of equal length. (See Figure 4.)

Some notes on the Consolidate procedure:

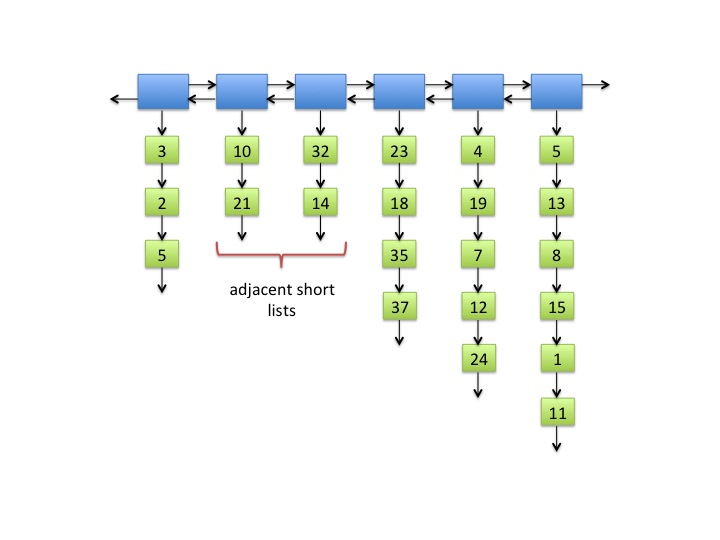
Fig. 2: A square list with adjacent short inner lists. Note that 2 < √22/2 ≈ 2.345.

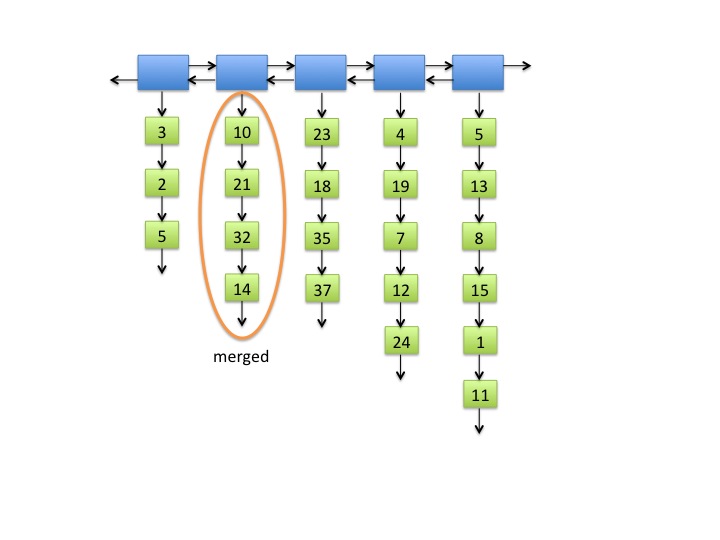
Fig. 3: Adjacent short lists merged.

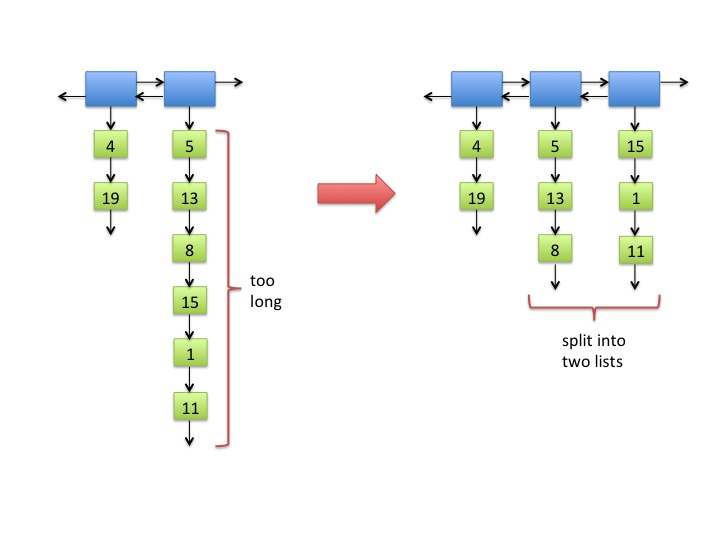
Fig. 4: A long inner list split into two lists. Note that 6 > 2 √8 ≈ 5.657.

Assignment

Note: Running time is one of the most important considerations in the implementation of a data structure. Programs that produce the desired output but exceed the required running times are considered wrong implementations and will receive substantial deductions during grading.

Your assignment is to implement a square list data structure as described above that hold integer values (more on "integer" later). Both the top-level list and the inner lists should be implemented using the C++ STL list templated container class.

This assignment specifies the interface between the main program and your square list implementation, but you are free to design the class as you wish, subject to some requirements below. In particular, you are not provided with a header file for the square list class. Note that design is part of the grading criteria, so you do need to apply good design principles to your inner list data structure.

Requirement: Your square list class must be called SqList. The class definition must be placed in a file called SqList.h and the member functions must be implemented in a file called SqList.cpp. File names are case-sensitive on GL.

Requirement: Your square list class must store the square list in a list of lists. Your SqList class definition must have the declaration:

list< list<Int341> > L ; We are omitting the traditional m_ before this data member's name because you will type its name so often. More on Int341 below.

Requirement: You are given the class definition and implementation of the Int341 class in Int341.h and Int341.cpp. You may not change these files in any way.

Requirement: You must have a member function named consolidate with the following signature in your SqList

void consolidate() ; You must place your code for the consolidate process described above in this function. (This is so the graders can find where you implement the consolidate process.) The consolidate function must not directly or indirectly invoke the constructor, copy constructor or the assignment operator of the Int341 class. This member function should run in O(√n) time not counting splits. The splits should take time proportional to the length of the inner list that is split.

Requirement: You must have a public member function named inspector with the following signature in your SqList class definition:

void inspector() ; This member function will be implemented by the grading programs, so you should not implement inspector(). It must be public so it can be called by the grading programs. Since inspector() is a member function, it will have access to SqList data members, in particular, it has access to L.

Requirement: Your code must not have any memory leaks. When you run your code under valgrind on GL, it must report:

All heap blocks were freed -- no leaks are possible

Requirement: Your implementation must be efficient. The running time for n operations with n data items stored in the SqList must be O(n √n). (See "How to Submit" below.)


Specifications

In addition to the requirements above, your SqList class must have the following member functions with the specified function signatures and running times:

  • A default constructor that initializes a SqList properly. It should run in O(1) time.

  • A copy constructor with the signature SqList(const SqList& other) ; The running time of the copy constructor must be O(n). (I.e., copy, do not insert n times.)

  • An overloaded assignment operator with the signature const SqList& operator=(const SqList& rhs) ; The running time of the assignment operator must be O(n).

  • A destructor may or may not be required. This depends on your design. In any case, your implementation must not leak memory.

  • A member function consolidate() as described above.

  • Two member functions to insert at the beginning and at the end of a SqList with the following signatures:

    void addFirst (const Int341& x) ; void addLast (const Int341& x) ;

    These member functions should call consolidate() after insertion. They must run in constant time, not counting the time for consolidate().

  • Two member functions to remove an item at the beginning and at the end of a SqList with the following signatures:

    Int341 removeFirst () ; Int341 removeLast () ;

    These functions must return the Int341 value that was stored at the beginning and the end of the list. If the list is empty, then they should throw an out_of_range exception. These member functions should call consolidate() after removal. They should run in constant time, not counting the time for consolidate().

  • A member function to insert an item at a given position of a SqList.

    void add(int pos, const Int341& data) ;

    Positions start at 0. Thus, add(0,Int341(5)) should insert 5 at the beginning of the list. Also, if a square list originally held 1, 2, 3, 4, 5, then after add(2,99) the list should hold 1, 2, 99, 3, 4, 5. If pos equals the number of items in the SqList, then data should be added to the end of the list. If pos is not valid, throw an out_of_range exception. This function should call consolidate() after insertion. The add() function should take time O(√n) not counting the time for consolidate().

  • A member function to remove an item from a given position of a SqList and return its value.

    Int341 remove(int pos) ;

    As with add(), positions start at 0. So, if a square list originally held 1, 2, 3, 4, 5, then after remove(3) the list should hold 1, 2, 3, 5. If pos is not valid, throw an out_of_range exception. This function should call consolidate() after removal. The remove() function should take time O(√n) not counting the time for consolidate().

  • An overloaded [] operator.

    Int341& operator[](int pos) ;

    As with add(), positions start at 0. So, if a SqList S originally held 1, 2, 3, 4, 5, then S[2] should return 3. Since a reference is returned, this [] can also be used to modify the SqList. For example, S[2] = Int341(777) ; should make the list 1, 2, 777, 4, 5. If pos is not valid, throw an out_of_range exception. The [] operator should take time O(√n).

  • A member function that returns the position of the first occurrence of a value in a SqList.

    int indexOf(const Int341& data) ;

    If data does not appear in the list, then return -1. As with add(), positions start at 0. So, if a square list originally held 1, 2, 3, 4, 5, then indexOf(5) should return 4. The indexOf() function should run in O(n) time.

  • A member function that returns the number of items in a SqList.

    int numItems() ;

    The numItems() function should run in constant time. This is used in grading.

  • A debugging member function:

    void dump() ;

    The dump() member function should print out the number of items in the SqList and for each inner list, the size of the inner list, each item in the inner list. (See sample output for recommended format.) The running time of dump() does not matter since it is used for debugging purposes only. However, you should implement dump() in the most reliable manner possible (i.e., avoid calls to member functions which might themselves be buggy).

  • The member function inspector() as described above.

    void inspector() ;

    Implementation Notes

    Before we list some recommendations and point out some traps and pitfalls, let's discuss Int341 and why we have it. One of the pitfalls of using STL container classes (and object-oriented programming in general) is unintentional copying. The Int341 class has just an int for its payload data. Its purpose is to allow us to track the number of times that the constructor, copy constructor, destructor and assignment operators are called. Consider the following main program that uses 5 different methods for retrieving the last item of a list<Int341> list. The report() member function of Int341 prints out the number of times that Int341 objects were created, copied and destroyed. (See Int341.h and Int341.cpp.) Note that the last two methods, using a reference and a pointer respectively, do not increase the number of calls.

    //File: test341.cpp // // UMBC Fall 2017 CMSC 341 Project2 // // Use the Int341 class to monitor the amount of copying // that takes place when you use the STL list class. // #include <iostream> #include <list> #include "Int341.h" using namespace std ; int main() { list<Int341> L ; Int341::m_debug = true ; L.push_back(Int341()) ; L.push_back(Int341()) ; L.push_back(Int341()) ; cout << "End of push_back's\n" ; Int341::report() ; cout << "\nMethod #1\n" ; Int341 a ; a = L.back() ; Int341::report() ; cout << "\nMethod #2\n" ; Int341 b = L.back() ; Int341::report() ; cout << "\nMethod #3\n" ; Int341 c(L.back()) ; Int341::report() ; cout << "\nMethod #4\n" ; Int341 &ref = L.back() ; Int341::report() ; cout << "\nMethod #5\n" ; Int341 *ptr ; ptr = &L.back() ; Int341::report() ; cout << "\nEnd of main\n" ; return 0 ; }

    Output:

    __Int341__ Constructor called __Int341__ Copy constructor called __Int341__ Destructor called __Int341__ Constructor called __Int341__ Copy constructor called __Int341__ Destructor called __Int341__ Constructor called __Int341__ Copy constructor called __Int341__ Destructor called End of push_back's __Int341__ Report usage: __Int341__ # of calls to constructor = 3 __Int341__ # of calls to copy constructor = 3 __Int341__ # of calls to destructor = 3 __Int341__ # of calls to assignment operator = 0 Method #1 __Int341__ Constructor called __Int341__ Assignment operator called __Int341__ Report usage: __Int341__ # of calls to constructor = 4 __Int341__ # of calls to copy constructor = 3 __Int341__ # of calls to destructor = 3 __Int341__ # of calls to assignment operator = 1 Method #2 __Int341__ Copy constructor called __Int341__ Report usage: __Int341__ # of calls to constructor = 4 __Int341__ # of calls to copy constructor = 4 __Int341__ # of calls to destructor = 3 __Int341__ # of calls to assignment operator = 1 Method #3 __Int341__ Copy constructor called __Int341__ Report usage: __Int341__ # of calls to constructor = 4 __Int341__ # of calls to copy constructor = 5 __Int341__ # of calls to destructor = 3 __Int341__ # of calls to assignment operator = 1 Method #4 __Int341__ Report usage: __Int341__ # of calls to constructor = 4 __Int341__ # of calls to copy constructor = 5 __Int341__ # of calls to destructor = 3 __Int341__ # of calls to assignment operator = 1 Method #5 __Int341__ Report usage: __Int341__ # of calls to constructor = 4 __Int341__ # of calls to copy constructor = 5 __Int341__ # of calls to destructor = 3 __Int341__ # of calls to assignment operator = 1 End of main __Int341__ Destructor called __Int341__ Destructor called __Int341__ Destructor called __Int341__ Destructor called __Int341__ Destructor called __Int341__ Destructor called

    The main point here is that your consolidate() function should not copy any data items. In particular, when you split and merge inner lists, you should not increase the number of calls to the Int341 constructor, copy constructor, destructor or assignment operator. You can check this by calling Int341::report() before and after you call consolidate.

    Now we list some recommendations and point out some traps and pitfalls:

    • Apply the incremental programming methodology. Implement one or two member functions and fully debug them before writing more code.

    • Carefully study the documentation for the STL list container class (e.g., here). Pay attention to the parameters, return values and the effect that a call would have on iterators. Make sure that you understand iterators and how to use them. There are often several ways to do the same thing with these member functions. You should choose the option that is more efficient and avoids copying.

    • Do look at the splice member function for the list class.

    • If you are not sure what a list member function does, write a small program that uses the function to test it.

    • Review what the list destructor does and when it is invoked.

    • The consolidate() function is the hardest. Think through the logic carefully before you code. For example, it is possible to have 3 short inner lists in a row. (How?) Would your consolidate() handle this case correctly? What are some other "weird" cases?

    Testing

    In Project 1, you were given an extensive suite of test programs. This is to provide you with an example of how you can test your code. For this project, you will have to write your own test program. The test program we provide below is just to make sure that your code will compile with the grading programs. Rest assured that the grading programs will exercise your code vigorously.

    Test programs:

    How to Submit

    You only need to submit two files: SqList.cpp and SqList.h. If for some reason you want to define new classes and additional functions, put all the declarations in SqList.h and all the implementations in SqList.cpp.

    Do not submit Int341.h or Int341.cpp since those should not have changed.

    We need a C++11 compiler to correctly perform the timing runs for this project. Instead of logging into the GL machines, log into one of fedora1.gl.umbc.edu, fedora2.gl.umbc.edu or fedora3.gl.umbc.edu. You can use the same username and password that you use on GL. The directory structure is the same as on GL. If you have customized your shell environment, some of your customizations might be broken, but you should still be able to run the g++ compiler. That is all we need. If you really cannot log into the fedora machines, then just use GL to record your timing runs.

    If you followed the instructions in the Project Submission page to set up your directories, you can submit your code using this Unix command:

    cp SqList.h SqList.cpp ~/cs341proj/proj2/

    Use the Unix script command to show that your code compiles. Also run valgrind on p2comptest.cpp and time the 3 timing programs.

    fedora2% cd ~/cs341proj/proj2/ fedora2% script Script started, file is typescript fedora2% g++ -include ../../00Proj2/Int341.h -I ../../00Proj2/ -I . ../../00Proj2/Int341.cpp SqList.cpp ../../00Proj2/p2comptest.cpp -o t0.out fedora2% g++ -include ../../00Proj2/Int341.h -I ../../00Proj2/ -I . ../../00Proj2/Int341.cpp SqList.cpp ../../00Proj2/p2timetest1.cpp -o t1.out fedora2% g++ -include ../../00Proj2/Int341.h -I ../../00Proj2/ -I . ../../00Proj2/Int341.cpp SqList.cpp ../../00Proj2/p2timetest2.cpp -o t2.out fedora2% g++ -include ../../00Proj2/Int341.h -I ../../00Proj2/ -I . ../../00Proj2/Int341.cpp SqList.cpp ../../00Proj2/p2timetest3.cpp -o t3.out fedora2% valgrind ./t0.out ... fedora2% time ./t1.out 0.293u 0.005s 0:00.51 56.8% 0+0k 0+0io 0pf+0w fedora2% time ./t2.out 1.111u 0.000s 0:02.26 49.1% 0+0k 0+0io 0pf+0w fedora2% time ./t3.out 4.303u 0.008s 0:08.11 53.0% 0+0k 0+0io 0pf+0w fedora2% fedora2% exit exit Script done, file is typescript

    Do remember to exit from the script command. This creates a file called typescript that will record any compilation errors. Yes, we know you can edit this file, but the compilation errors will just show up when we compile the programs again and you will still get lots of points deducted. This step is to compel you to fix any changes needed to get your program to compile on GL without any errors.

    Note: cd to the appropriate directory if you are submitting late.

    Now you can delete the executable files with

    rm t?.out

    Then you should just have 3 files in your submission directory. Check using the ls command. You can also double check that you are in the correct directory using the pwd command. (You should see your username instead of xxxxx.)

    fedora2% ls SqList.cpp SqList.h typescript fedora2% pwd /afs/umbc.edu/users/c/h/chang/pub/cs341/xxxxx/proj2 fedora2%


    A Note on Timing

    The main programs for timing above ( p2timetest1.cpp, p2timetest2.cpp and p2timetest3.cpp) double the number of items and the number of calls to SqList member functions each time. Since we expect the total running time to be O(n √n), doubling the value of n should increase the total running time by a factor of approximately 2.82. This is because

        2n √ 2n = 2 √2 n √n

    and 2 √2 ≈ 2.82. On some systems (e.g., Mac OS X), the running times bear this out:

    MyMacBook% time ./t1.out 0.978u 0.002s 0:00.98 98.9% 0+0k 0+0io 0pf+0w MyMacBook% time ./t2.out 2.814u 0.003s 0:02.81 100.0% 0+0k 0+0io 0pf+0w MyMacBook% time ./t3.out 8.201u 0.007s 0:08.20 100.0% 0+0k 0+0io 0pf+0w

    The ratios 2.814/0.978 ≈ 2.877 and 8.201/2.814 ≈ 2.914 are quite close to the predicted value of 2.82.

    However, it turns out that the Standard Template Library is not so standard. (See note on GNU website.) In particular the running time of the size() function may be O(1), which is what we want, or O(n), which is what is on GL. So, timing the same programs on GL gives quadratic running time.

    linux3% time t1.out 0.292u 0.000s 0:00.29 100.0% 0+0k 0+0io 0pf+0w linux3% time t2.out 1.122u 0.000s 0:01.12 100.0% 0+0k 0+0io 0pf+0w linux3% time t3.out 4.248u 0.000s 0:04.25 99.7% 0+0k 0+0io 0pf+0w

    Each successive run gives roughly quadruples the running time: 1.122/0.292 ≈ 3.84 and 4.248/1.122 ≈ 3.786. Your implementation should assume that size() takes O(1) time.

    Discussion Topics

    Here are some topics to think about to help you understand square lists. You can discuss these topics with other students without contradicting the course Academic Conduct Policy.

    1. Suppose you start with an empty square list and keep inserting items in the front of the list. When does the first merge occur?

    2. What is the smallest number of items you can have in a square list that has 11 inner lists?

    3. Do we ever encounter long inner lists that have to be split (other than the first inner list) if we only allowed insertion and removal at the beginning of the list?

    4. After you split an inner list, is it possible that the same inner list has to be split again after the very next square list operation? after two operations? when could the next split occur?

    5. Can you ever encounter 3 short lists in a row during the Consolidate procedure? Does it matter? and should you write code whose correctness depends on the answer to these questions?