Research Overview
This webpage is designed to give an overview of the broad array of topics that I work on.
My focus is on modeling signaling within excitable media. This has a range of applications specifically within neuroscience, cardiac physiology, and pancreatic beta-cell dynamics. I am currently involved with the UBM program at UMBC where we are studying border cell migration with JAK/STAT signaling in drosophila ovaries as a model system for some forms of cancer migration. Some other projects have been switching aerobic states of facultative anarobe E.coli, and vitamin D buffering and antimicrobial protein activation in monocytes.
I use mathematical tools such as dynamical systems/ordinary differential equations, partial differential equations, bifurcation theory, perturbation theory, numerical solutions, and simulation to advance scientific understanding of nonlinear systems. This in turn feeds back on mathematical developments.
Neuroscience
Calcium Waves in Main Apical DendriteMy work in neuroscience has focused on modeling related to experiments, some of which have been done in Bill Ross' lab, on calcium wave generation. Calcium is a ubiquitous second messenger, and its function in long term potentiation and even longer term structural changes is well studied. I have developed a one-dimensional PDE model of calcium handling in the main apical dendritic trunk with a point source at an oblique dendrite.[1] I am currently updating the model to reflect the effect of priming on the calcium wave initiation which requires the modeling of the dynamic store of calcium interior to the cell.
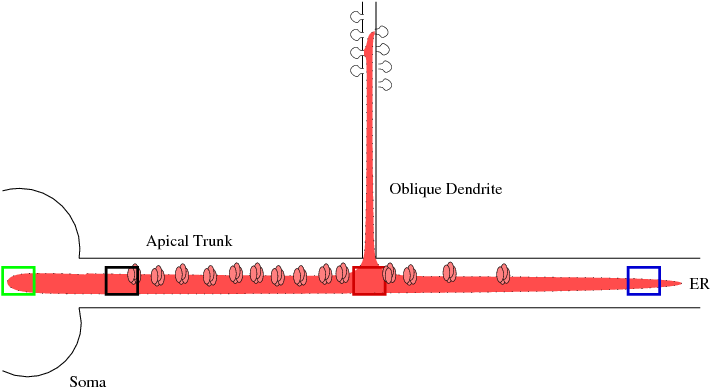
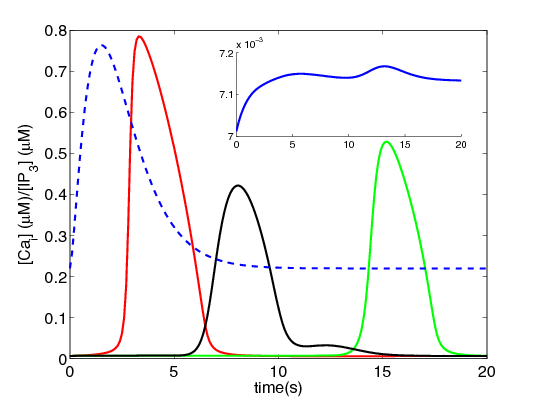

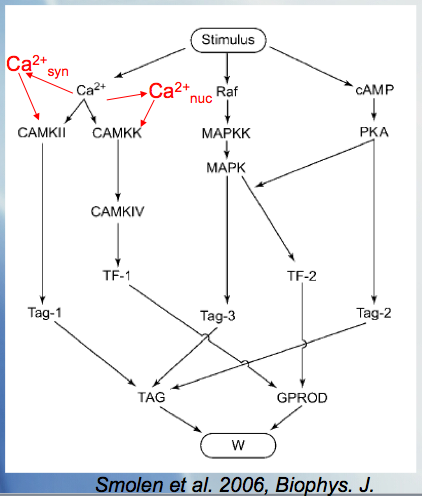
We have merged Paul Smolen's model of LTP [2] with the current calcium wave model to look at different mechanisms of potentiation at increasing time scales as seen experimentally, for example, in Raymond and Redman [3].
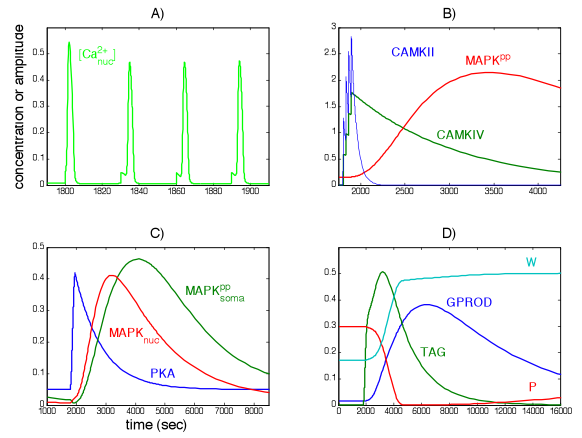
Recently collaborators have experimental results exploring the synchrony of calcium oscillations in a network of cortical cells. They alternately enhance and knock out communication between cells and apply mechanical deformation to the preparation to understand the effect of blunt force trauma to the brain. We have begun to consider a multicellular mathematical model preparation designed to predict effects of communication disruptions and trauma.
- Bradford E. Peercy, Initiation and Propagation of an Intracellular Neuronal Calcium Wave, J. Comput. Neurosci., 2008 Oct 25(2):334-48., link
- Paul Smolen, Douglas A. Baxter, and John H. Byrne,A Model of the Roles of Essential Kinases in the Induction and Expression of Late Long-Term Potentiation,Biophys J. 2006 April 15; 90(8): 2760–2775.
Published online 2006 January 13. doi: 10.1529/biophysj.105.072470.
- Clarke R. Raymond and Stephen J. Redman,Spatial segregation of neuronal calcium signals encodes different forms of LTP in rat hippocampus,J. Physiol. 2006;570;97-111; originally published online Nov 10, 2005.
Cardiac Physiology
Spontaneous Stochastic Calcium Waves in a Cardiac Cell with Zana Coulibaly (grad student) and Matthias Gobbert, UMBCMatthias Gobbert has numerically implemented a long time behavior model of calcium dynamics in a heart cell. This is a 3-D partial differential equation model with stochastic release sites [1]. Current experiments show spontaneous wave generation in isolated cardiac cells. This is relevant to mechanisms of cardiac arrhythmias from calcium store overload, and we are actively pursuing more biophysical reality in the model to reflect this.
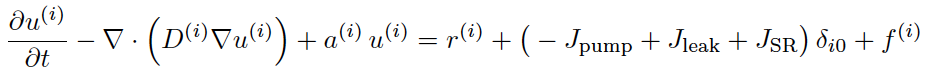
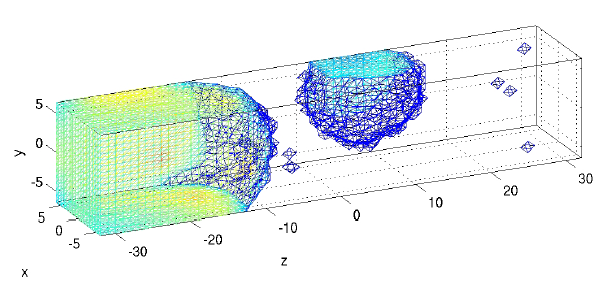
Top: Generic partial differential equations used for cytosolic calcium and two buffering species.
Bottom: Initiation of two wave fronts of calcium at 200 ms.
We study a theoretical mechanism for an arrhythmia at the border between healthy and sick tissue. As a system of coupled cells or the more general coupled tissue mass, we have a specified conditions for anomalous electrical activity for the sick/healthy system given certain behavior of normal tissue under stimulation [2]. We use dynamical systems, bifurcation theory, and numerical continuation to approach this problem. The mathematical mechanism is a Hopf bifurcation during a rise in extracellular potassium.
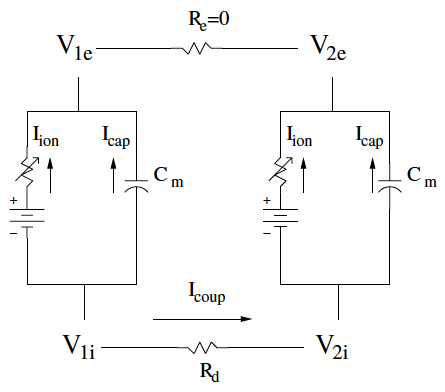
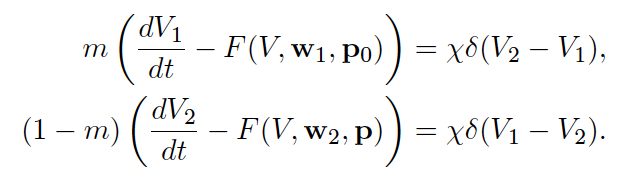
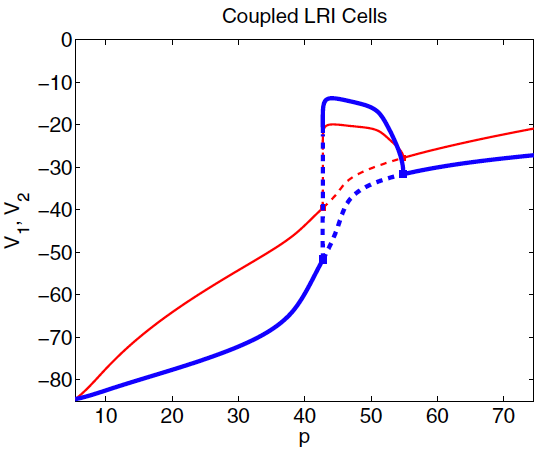
Left: Schematic of electrical coupling of two cardiac cells.
Middle: Ordinary differential equations for the coupled cells.
Right: Bifurcaiton diagram for the voltages of the two coupled cells while altering "degree of sickness" parameter.
For p>43 we see the loss of the stable steady state and the system begin oscillating.
We would like to extend the result to a 1-D partial differential equation model that represents strip of tissue experiments.
There are potential collaborations with UMBC biology faculty on Drosophila (fly) heart function. This physiology is different from that of mammal but there are potential insights to be gained at multiple levels including understanding from genetic code to organ function. This has the potential to inform a comprehensive model. Information on recent experimental work from other labs may be found in [3].
- Matthias K. Gobbert. Long-Time Simulations on High Resolution Meshes to Model Calcium Waves in a Heart Cell. SIAM Journal on Scientific Computing, vol. 30, no. 6, pp. 2922-2947, 2008.
- Bradford E. Peercy and James P. Keener, Coupled Cell Model of Border Zone Arrhythmias, SIAM J. Appl. Dyn. Syst. 4, 679 (2005), DOI:10.1137/040615973 link (or here)
- Wasserthal, Lutz T., Drosophila flies combine periodic heartbeat reversal with a circulation in the anterior body mediated by a newly discovered anterior pair of ostial valves and `venous' channels, J Exp Biol 2007 210: 3707-3719
- Vaughan-Jones RD, Peercy BE, Keener JP, Spitzer KW, Intrinsic H(+) ion mobility in the rabbit ventricular myocyte, J Physiol. 2002 May 15;541(Pt 1):139-58. link
- Spitzer KW, Skolnick RL, Peercy BE, Keener JP, Vaughan-Jones RD, Facilitation of intracellular H(+) ion mobility by CO(2)/HCO(3)(-) in rabbit ventricular myocytes is regulated by carbonic anhydrase, J Physiol. 2002 May 15;541(Pt 1):159-67.link
Pancreatic Beta Cell and Islet Physiology
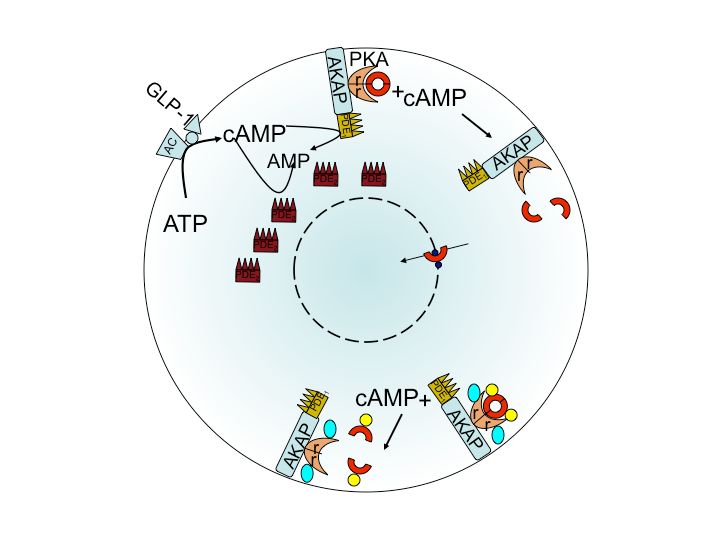
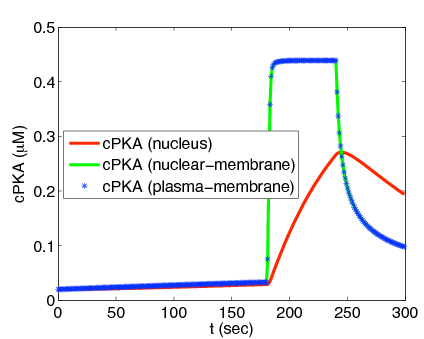
Long time scale signaling from Membrane to Nucleus in Beta cells with Artie Sherman, NIH
Next to calcium cyclic-adenosine monophosphate (cAMP) is the most ubiquitous second messenger. One of its two targets is Protein Kinase A (PKA) where it dissociates the catalytic subunit (cPKA) from regulatory subunit. From its anchor on the membrane, cPKA activates many processes at the membrane but there is also translocation to the nucleus. In the nucleus it activates cAMP response element binding protein to act as a transcription factor facilitating beta cell proliferation.
Experiments show little nuclear cPKA with a 1 min, cAMP-producing pulse every 4 min, while sustained cAMP produces significant cPKA in the nucleus. In our work we show that delay from rapid buffering at the nuclear membrane can account for the data. Time scale and perturbation analysis suggest further experiments based on alterations in cAMP forcing.[1]
Further modeling developments will include mechanism of calcium activation of both cAMP production and degradation as the natural mechanism for PKA signaling.
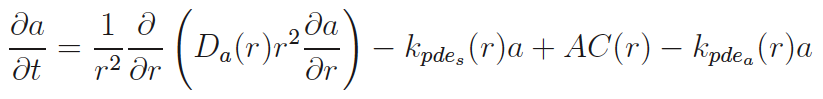
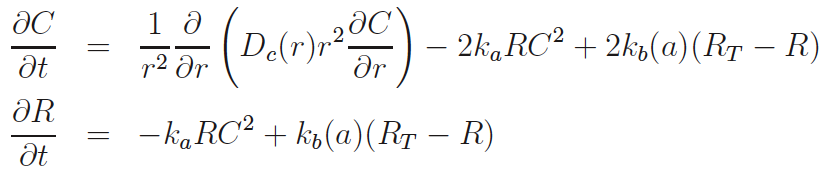
Due to computational restrictions it has proven difficult to get a numerical implementation of a full pancreatic islet but with flexibility to explore varying hypotheses of the biophysics. Typically we invoke strong electrical coupling between beta cells to write a single system of ordinary differential equations for an islet (primarily a group of beta cells). However, there are questions that should be addressed such as, how does the parameter variability between uncoupled beta cells within an islet affect the overall coupled islet behavior?
- Bradford E. Peercy and Arthur Sherman, How Pancreatic Beta Cells Discriminate Long- and Short-Time Scale cAMP Signals: The Nuclear Membrane as a Diffusional Barrier to the Catalytic Subunit, to be submitted to Biophysical Journal.
- Zhang M, Fendler B, Peercy B, Goel P, Bertram R, Sherman A, Satin L, Long lasting synchronization of calcium oscillations by cholinergic stimulation in isolated pancreatic islets, Biophys J. 2008 Nov 15;95(10):4676-88. Epub 2008 Aug 15
Other Topics
Vitamin D as Genetic Regulator with Rene Chun, UCLA
Vitamin D levels affect cellular functions such as proper calcium absorption. Vitamin D level in a cell is dictated by the levels of albumin and vitamin D binding protein, buffers of vitamin D. We use a steady state model to predict the intracellular levels of vitamin D given differing amounts of buffer, total vitamin D, and dissociation constants. We compare this to gene transactivation data. Further model developments may be necessary to explain new data in mice.
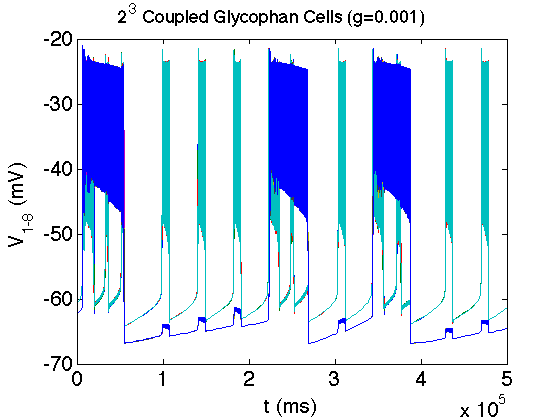
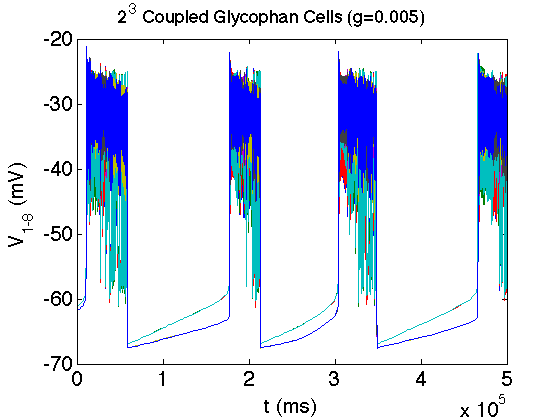
The bacterium E. coli has the ability to adapt to low/no oxygen environments. It is able to switch between terminal electron acceptors in the electron transport chain of respiration. To do this, critical transcription factors such as ArcAB and FNR regulate cytochrome production. We have shown the existence of a bistable region in oxygen at a semi-aerobic state which may be a cause for hysteresis in switching states.[1]
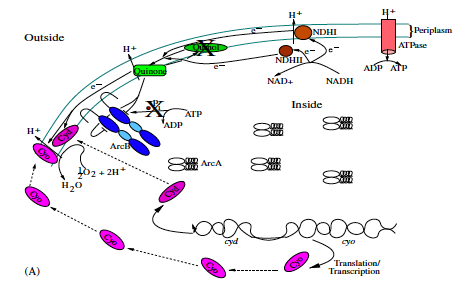
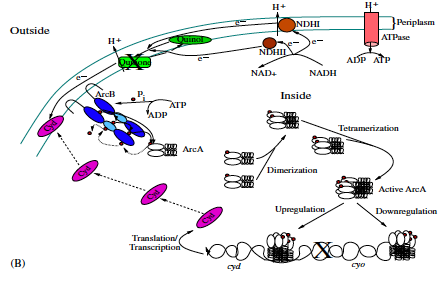

- Bradford E. Peercy, Steven J. Cox, Sagit Shalel-Levanon, Ka-Yiu San, George Bennett, A Kinetic Model of Oxygen Regulation of Cytochrome Production in Escherichia coli, J Theor Biol, 2006 Oct 7;242(3):547-63. link
- Cox SJ, Shalel Levanon S, Sanchez A, Lin H, Peercy B, Bennett GN, San KY, Development of a metabolic network design and optimization framework incorporating implementation constraints: a succinate production case study, Metab Eng. 2006 Jan;8(1):46-57. Epub 2005 Nov 2.link